†Corresponding author. E-mail: 2010thzz@sina.com
*Project supported by the National Natural Science Foundation of China (Grant No. 11304397).
Passive decoy-state quantum key distribution is more desirable than the active one in some scenarios. It is also affected by the imperfections of the devices. In this paper, the influence of modulator attenuation on the passive decoy-state method is considered. We introduce and analyze the unbalanced Mach–Zehnder interferometer, briefly, and combining with the virtual source and imaginary unitary transformation, we characterize the passive decoy-state method using a weak coherent photon source with modulator attenuation. According to the attenuation parameter δ, the pass efficiencies are given. Then, the key generation rate can be acquired. From numerical simulations, it can be seen that modulator attenuation has a nonnegligible influence on the performance of passive-state QKD protocol. Based on the research, the analysis method of virtual source and imaginary unitary transformation are preferred in analyzing passive decoy state protocol, and the passive decoy-state method is better than the active one and is close to the active vacuum + weak decoy state under the condition of having the same modulator attenuation.
Quantum key distribution (QKD)[1, 2] allows two legal communication parties, Alice and Bob, to establish a common and secret key when the channel is accessible to an eavesdropper, Eve. It is an important part of quantum cryptography. Compared with the classical cryptography, the biggest advantage of quantum cryptography is the unconditional security which is based on the fundamental laws of physics: no-cloning theorem and uncertainty principle.[3]
Since Bennett and Brassard proposed the best-known protocol— BB84 protocol, [1] quantum cryptography has developed well both theoretically and experimentally.[4– 11] The unconditional security of QKD protocol was given by Lo H K and Chau H F, [12] first. It was based on the situation that Alice and Bob both have the quantum computers, which is still commercially unavailable with current technology. Hence, people wanted to find some other ways to prove the unconditional security. Shor P and Preskill J[5] gave the proof that the security of QKD protocol based on state preparation and state measurement is equal to that of QKD protocol based on entanglement purification. Combined with the CSS (Calderbank– Shor– Steane) codes and entanglement purification, the unconditional security can be proven by current correction technology. Renner et al.[13] used the information theory to prove the unconditional security which gives the upper bound of the amount of information that Eve can get. In 2008, Horodecki et al.[14] first proved that QKD protocol can generate a security key when there is no entanglement purification.
The proofs of the unconditional security of QKD protocol are based on the ideal condition.[15] This means the single-photon source, the perfect detector, the safe and credible channel, and so on. However, in the real situation, the conditions mentioned before are not easy to satisfy. There are many unavoidable imperfections in a practical QKD system like multi-photon pulse, attenuation of detector, non-authenticated channel, and finite resources. They undoubtedly threaten the security of QKD. Therefore, researching the impact of the factors in real conditions on the security of QKD system is important.
To analyze the influencing factors as mentioned, some researchers improved the original protocols or presented new protocols such as decoy-state protocol[16– 20] and device-independent QKD (DI-QKD).[21– 31] Some other researchers used the mathematical and information knowledge to characterize the impact of the imperfect factors on the security of QKD by a security proof.
In this paper, we analyze the security of the passive decoy-state method[32, 33] based on the phase-coding protocol[34] under the condition of modulator attenuation. The phase-coding protocol where the unbalanced Mach– Zehnder interferometer (UMZI)[35, 36] is commonly used is more stable than the polarization one. The UMZI is composed of two parts: a long arm and a short arm. In the ideal station, we consider that the attenuation of the short arm is equal to that of the long arm. However, due to the imperfect phase modulator (PM) in the long arm, it will introduce more loss than the short arm. The security of QKD system is affected.
Currently, the method for analyzing modulator attenuation is mainly to establish a new model to replace the original actual phase modulator. The new model is more easy to analyze. In 2010, Li et al.[37] presented imaginary unitary transformation and virtual source to analyze the security of BB84 protocol. Ferenczi et al.[38] provided a qubit-based security proof on unbalance BB84 protocol. In this paper, the imaginary unitary transformation and virtual source model are introduced to the passive decoy-state method, and the security of passive decoy-state method with modulator attenuation is also analyzed.
The rest of this paper is organized as follows: In Section 2 and Section 3, we introduce the decoy-state protocol and the WCP source that can be used in the passive decoy-state method, respectively. In Section 4, we recall the UMZI model and analyze it with the method that using a perfect PM and an unbalanced attenuator replace the imperfect PM. We consider the passive decoy-state method with imaginary unitary transformation and virtual source under the modulator attenuation condition in Section 5. Finally, Section 6 gives a summary of this paper.
It has been noted that the necessary assumptions that the ideal QKD system needs are not easy to satisfy. In the original proposal of the BB84 protocol, a single-photon source is necessary. However, the single-photon source is still unavailable with the current technology. A weak coherent pulse (WCP) source was used instead and many WCP-based experiments have been done since the first QKD experiment.[39] However, due to the multiphoton pulses sent by WCP source, the QKD system will suffer from photon-number splitting (PNS) attack.[40, 41] To protect QKD system from PNS attack, one can use the decoy-state method which could closely reach the performance of single-photon sources. Actually, the initial decoy-state method can be called active decoy-state method in which Alice prepares the decoy states actively. However, due to the “ active” process, it may bring some side channel information that Eve can make use of to have an attack. For the real active (regular) decoy-state experiments, it is more difficult to verify the assumption that Eve cannot distinguish decoy and signal states.[42]
To solve this problem, the passive decoy-state method was presented. It can reduce the side channel information in the decoy-state preparation procedure. Different from the active decoy-state method which actively changes the intensity of the laser pulses randomly, the passive decoy-state method only has one intensity pulse. The key point to distinguish in the passive decoy-state method is clicking or no clicking for Alice’ s detector.
The common point between the passive decoy state and the active decoy state is that the counting rates and the error rates of the pulse of the same photon-number states from the signal states and the decoy states shall be equal to each other, [17]
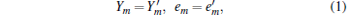 |
where Ym and 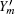
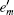
In 2005, Lo et al.[17] combined the decoy state method with the results provided by the Gottesman– Lo– Lü tkenhaus– Preskill (GLLP)[6] analysis and gave the exact formula for secure key generation rate as follows:
 |
where Rl satisfies
 |
The parameter q is the efficiency of the protocol. For the standard BB84 protocol, [1]q = 1/2, f (El) denotes the efficiency of the error correction protocol as a function of the error rate El, [43] typically f (El) ≥ 1 with Shannon limit f (El) = 1 (usually, we set 1.22 as its approximate value), e1 denotes the single photon error rate, H2 (x) = − xlog2 (x) − (1 − x) log2 (1 − x) is the binary Shannon entropy function.
In this paper, we define that c denotes “ click” of the detector while c̄ denotes “ no click” . We denote the signals that cause a click of Alice’ s detector as signal states. The ones that cause no click of Alice’ s detector are decoy states.
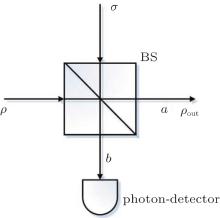
Due to the characters of the WCP source itself, it cannot be used for the passive decoy-state method directly. Curty et al.[42, 45] have adjusted the WCP source to make it output two Fock diagonal states, so that it can be used for the passive decoy-state method. The fundamental setups are shown as follows.
In Fig. 1, ρ and σ denote the coherent states of two phase-randomized WCP source states, respectively,
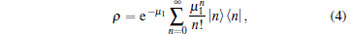 |
 |
with μ 1 and μ 2 denoting the mean photon numbers of the two signals, respectively. It should be noted that the WCP source that Curty et al. have changed is phase-randomized WCP. Without additional explanations, the WCP source mentioned throughout this paper is the source which is shown in Fig. 1. We consider the threshold detector as the photon-detector in Fig. 1. In this scenario, the joint probability of having n photons in output mode a and m photons in output mode b can be written as[45]
 |
where the parameters υ , γ , and ξ are given by
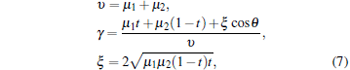 |
and t denotes the transmittance of a beam splitter.
Whenever the sender, Alice, does not protect the result of the measurement in mode b, the probability of having n photons in mode a can be written as
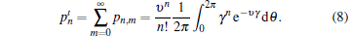 |
For Alice’ s detector, the joint probability of having n photons in mode a and no click in the threshold detector now has the form
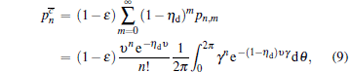 |
where the parameter ɛ denotes dark count and η d denotes the detection efficiency of the detector.
Then, the probability of having n photons in mode a and producing a click in Alice’ s threshold detector is
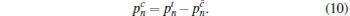 |
Currently, the practical QKD systems can be divided into phase-coding protocol[34] and polarization protocol. For comparison, the phase-coding protocol is more stable than the polarization one. Unbalanced Mach– Zehnder interferometer[35, 36] (UMZI) is commonly used. The fundamental setups are shown in Fig. 2.
UMZI is composed of a long arm and a short arm, where the long arm has a phase modulator (PM). In the proof of QKD’ s security, it is assumed that the attenuation of the long arm is equal to the one of the short arm, and Alice’ s attenuation has no effect on the security of QKD system. Bob’ s attenuation can belong to the attenuation of the channel. Theoretically, they do not affect the secure key generation of QKD. However, the practical PM in the long arm will introduce more loss, so that the attenuations are not equal. Under this condition, the photon states emitted from Alice are imperfect BB84 states. In this case, the key generation rate and security of QKD will be affected.
From Fig. 2, we can see that the photon states entering the quantum channel can be divided into photon states from the short arm and long arm, respectively. After the phase modulation of Bob’ s side, the two photon states are divided into four photon states. In this paper, we consider that the phase of the photon from the long arm is randomly modulated by 0, 0.5π , π or 1.5π in Alice’ s side. Because only the single photon state transmitted in the quantum channel can be used, the practical single photon state is
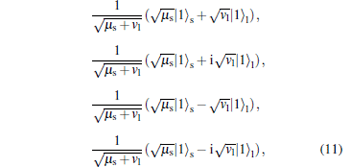 |
where | 1〉 s denotes the single-photon state in the short arm. | 1〉 l denotes the single-photon state in the long arm after PM, and μ s is the average source intensity of the short arm, and vl is the average source intensity of the long arm after PM.
As mentioned, the attenuation of the long arm is equal to the one of the short arm in the proof of QKD’ s security, i.e. μ s = vl. Due to the imperfection of the devices, the attenuation of the long arm is larger than that of the short arm. Therefore, μ s > vl. We call the photon states emitted from Alice unbalanced states.
A simple analytical model is replacing the practical PM in the long arm by a perfect PM and an unbalanced attenuator.[37]
The loss from the practical PM can belong to the unbalanced attenuator. Based on this, two hypotheses are: (i) The unbalanced attenuator can be controlled by the eavesdropper, Eve. (ii) The single-photon states emitted by Alice are ideal BB84 states. Based on the above assumptions, we can get the key generation rate
 |
where S is the probability distribution of the single-photon states when we consider that Alice’ s PM is perfect, α denotes the loss coefficient of the quantum channel, d represents the transmission distance, PA and PB are the pass efficiencies of Alice and Bob, respectively. Usually, they can be written as PA = (μ s + vl)/2μ and PB = vl/(μ s + vl). Theoretically, we consider that only the single-photon state emitted by Alice can generate the key bit. The multi-photon state has no contributions to the key generation. Note that the single-photon states attenuated from the multi-photon states by the unbalanced attenuator also cannot be used to generate the key bit. Combining the two hypotheses, the final key generation rate is low.
In this section, the idea of imaginary unitary transformation and virtual source[37] is introduced. Combined with the passive decoy-state method, we consider the influence on the security of the passive decoy-state method under the condition of modulator attenuation. Firstly, we will introduce imaginary unitary transformation and virtual source briefly. The fundamental setups are shown in Fig. 4. Reference [37] has proved that the practical photon states, i.e., the states in Eq. (11), are as secure as the perfect BB84 state when considering the practical state is equal to the perfect BB84 state combining with a unitary transformation.
Unitary transformation does not change the inner product of vectors, the eigenvalues or the eigenvectors of the matrix. An important application of unitary transformation in quantum mechanics is converted between different representations. The unitary transformation in Fig. 4 is a virtual structure, so there is no need to implement it in the practical QKD experiment. The unitary transformation is given as follows:
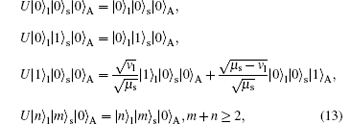 |
where | 0〉 A and | 1〉 A are mutually orthogonal states in Alice’ s side. They are emitted randomly. Alice does not know each state, and | n〉 s and | n〉 l denote the n-photon states in the short arm and the long arm, respectively, n means the number of the photon.
From Eq. (13), it can be seen that the unitary transformation does not change the vacuum state, multi-photon state, and single-photon state in the short arm. However, the single-photon state will be | 1〉 l | 0〉 s | 0〉 A with a probability of vl/μ s and | 0〉 l | 0〉 s | 1〉 A with a probability of (μ s − vl)/μ s after the unitary transformation.
Similar to Section 4, the average source intensity is changed from 2μ s to μ s + vl because of the imaginary unitary transformation. Therefore, the pass efficiency of the imaginary unitary transformation is PU = (μ s + vl)/2μ s.
In the model of imaginary unitary transformation and virtual source, the practical photon states in the quantum channel are regarded as the perfect BB84 states emitted by the virtual source and changed by unitary transformation.
After the phase randomization, the density matrix of the virtual source is
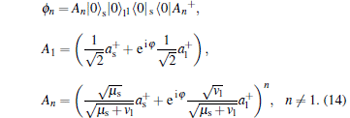 |
In this paper, the source considered is the WCP source in Section 3, so the single photon state of the virtual source emitted by Alice’ s side is given by
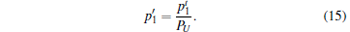 |
The probability distribution multi-photon state of the virtual source can be respectively expressed by
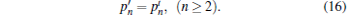 |
Next, we will analyze the key generation rate combining with passive decoy-state method.
From Eqs. (6)– (8), we can find that the joint probabilities are determined by the initial intensities μ 1 and μ 2, and it is difficult to obtain μ 1 and μ 2 from μ s and vl. To calculate the final key generation rate, we introduce a modulator attenuation parameter δ . Its expression is
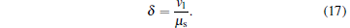 |
Then, the pass efficiencies of Alice and Bob can be regarded as the function of δ .
The distinction between signal state and decoy state is determined by the results of the detector in Alice’ s side
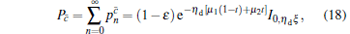 |
 |
where ɛ represents the dark count, η d denotes the detection efficiency of the detector, t is the transmittance of a beam splitter. In this paper, t = 1/2, Ia, b is the modified Bessel function of the first kind, [41]
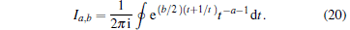 |
The Qc and Qc̄ are the overall gains of Alice’ s detector producing a click and no click, respectively, Qt denotes the overall gain that Alice ignores the result of her measurement in mode b. They can be expressed by
 |
 |
 |
Correspondingly, the error rates can be acquired as
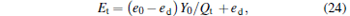 |
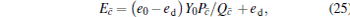 |
 |
where ω = μ 1t + μ 2 (1 − t), η sys denotes the overall transmittance of the system. It can be written as η sys = PAPBη channelη Bob, PA and PB represent the pass efficiencies of Alice and Bob, respectively, η Bob is the overall transmittance of Bob’ s detection apparatus, η channel can be related to a transmission distance d measured in km for the given QKD schemes as
where α represents the loss coefficient of the channel measured in dB/km.
In the ideal station, PA = 1 and PB = 1/2. However, they will change under the real condition. Here, we can see the essence of the modulator attenuation. The additional loss coming from the modulator of the long arm weakens the pulses, so that the pass efficiencies of Alice and Bob are changed. After all, the overall transmittance of the system is affected.
According to the GLLP formula, we can get the key generation rate as
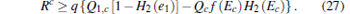 |
Due to the contributions of the decoy state in the passive decoy-state method, the key generation rate of the decoy state needs to be calculated
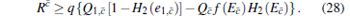 |
Finally, the key generation rate of the passive decoy-state method is
 |
In this section, some numerical simulations are taken to show how modulator attenuation influences the final key generation rate. In this scenario, the yield of n-photon state can be expressed as[17, 20]
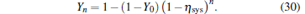 |
We set μ 1 = 0.5 and μ 2 = 0.0001. The other experimental QKD parameters are shown in Table 1. which come from Ref. [47].
| Table 1. Experimental QKD parameters. |
First, we will give a simulation of the passive decoy-state method in the ideal station. In this case, the PM in the long arm of UMZI will not introduce extra attenuation which means vl = μ s and δ = 1, so the pass efficiencies of Alice: PA = 1. For the phase-coding QKD protocol, only the interfering pulses, which produce clicks in the middle time (t2 in Fig. 5), are used for the key generation. The pass efficiencies of Bob: PB = 1/2.
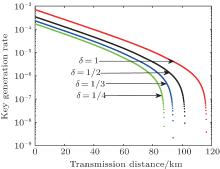
Then, we will simulate the method of replacing the practical PM in the long arm by a perfect PM and an unbalanced attenuator. Comparing with the virtual source, we also combine the method with the passive decoy-state method. In this case, due to the unbalanced attenuator, PA = (μ s + vl)/2μ s and PB = vl/(vl + μ s). It should be noted that we assume that the unbalanced attenuator can be controlled by Eve, so when we calculate the probability distributions of n-photon state, vl = μ s. Figure 6 gives the relationships between R and d of δ = 1/2, 1/3, 1/4, respectively. The curve of δ = 1 denotes the ideal condition.
Next, we shall give the numerical simulations of the passive decoy-state method with the method of imaginary unitary transformation and virtual source. In this case, we consider the practical PM which would introduce extra attenuation to the QKD system, so vl < μ s. It has been mentioned that the practical photon states in the quantum channel can been regarded as the perfect BB84 states emitted by the virtual source and changed by unitary transformation. Combined with the nature of unitary transformation, PA is equal to 1. PB = vl/(vl + μ s). Figure 7 shows the relationship between R and d of δ = 1/2, 1/3, 1/4, respectively. Similarly, the curve of δ = 1 denotes the ideal condition.
We compare the above cases when δ = 1/3. To get a better result, we define R(δ )/R as the fidelity of the passive decoy-state method considering modulator attenuation, where R(δ ) and R are the key generation rates with and without modulator attenuation.
According to Figs. 8 and 9, we can find that no matter which analytical method is chosen, the modulator attenuation will affect the key generation rate and transmission distance of practical QKD system. Comparing with the methods of unbalanced attenuator and virtual source, it shows that the method of virtual source is better than the method of unbalanced attenuator in the key generation rate and transmission distance.
 | Fig. 7. The relationship between key generation rate (R) and the transmission distance (d) of passive decoy-state method under the analysis of imaginary unitary transformation and virtual source. |
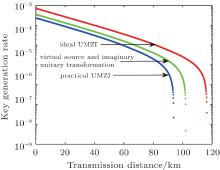 | Fig. 8. The relationship between key generation rate (R) and the transmission distance (d) of passive decoy-state method under different conditions. |
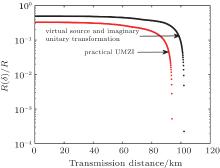 | Fig. 9. The relationship between R(δ )/R and the transmission distance (d) of passive decoy-state method under different conditions. |
Finally, we give the comparison of the R(δ )/R versus transmission distance among the one decoy-state, vacuum + weak decoy-state, and passive decoy-state methods when δ = 1/3. Figure 10 shows the answer. Based on Fig. 10, it can be seen that the passive decoy-state method is better than the active one decoy state when the extreme transmission distance is taken into consider. The d of the passive decoy-state method is a little smaller than that of the vacuum + weak decoy-state. If d > 60 km, the fidelity R(δ )/R of the passive decoy-state method is larger than the one of one decoy-state and is close to the R(δ )/R of vacuum + weak decoy-state. In a word, the passive decoy-state method is better than the one decoy-state and is close to the vacuum + weak decoy-state.
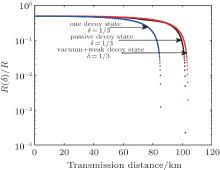 | Fig. 10. The relationships between R(δ )/R and the transmission distance (d) of passive decoy-state method, one decoy-state and vacuum + weak decoy-state. |
In summary, the passive decoy-state method with WCP source in the case of modulator attenuation is considered. Two safety equivalent models were used to analyze the attenuation of UMZI. One is replacing the practical PM in the long arm by a perfect PM and an unbalanced attenuator. The other one is an imaginary unitary transformation and virtual source. They were compared with the ideal situation and different attenuations. According to the numerical simulations, it seems that modulator attenuation has a nonnegligible influence on the final key rate of the passive decoy-state QKD protocol with WCP source. The larger the attenuation is, the smaller the key generation rate and extra transmission distance are. Besides, evidence shows that the analytical method of virtual source is better than the unbalanced attenuator one both in the key generation rate and transmission distance. Moreover, comparing with the active one decoy-state and the active vacuum + weak decoy-state methods, the result shows that the passive decoy-state method is better than the active one decoy state and is close to the active vacuum + weak decoy state under the condition of having the same modulator attenuation. The conclusions can be used for the actual operation of QKD systems.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|