†Corresponding author. E-mail: binzhou@hubu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11274102), the New Century Excellent Talents in University of Ministry of Education of China (Grant No. NCET-11-0960), and the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20134208110001).
We investigate the thermal entanglement in a spin-1/2 Ising–Heisenberg diamond chain, in which the vertical Heisenberg spin dimers alternate with single Ising spins. Due to the fact that the Dzyaloshinskii–Moriya (DM) interaction contributes to unusual and interesting magnetic properties in actual materials, and moreover it plays a significant role in the degree of the entanglement of the Heisenberg quantum spin systems, we focus on the effects of different DM interactions, including D z and D x, on the thermal entanglement of the Heisenberg spin dimer. The concurrence, as a measure of spin dimer entanglement, is calculated for different values of exchange interactions, DM interaction, external magnetic field, and temperature. It is found that the critical temperature and the critical magnetic field corresponding to the vanishing of entanglement increase with DM interaction, and the entanglement revival region gets larger by increasing DM interaction, thus DM interaction favors the formation of the thermal entanglement. It is observed that different DM interaction parameters ( D z and D x) have remarkably different influences on the entanglement. Different from the case D z, there is the non-monotonic variation of the concurrence with temperature in the case D x, and additionally the DM interaction D x can induce the entanglement near zero temperature in the case that the antiferromagnetic Ising-type interaction constant is larger than the antiferromagnetic Heisenberg interaction constant. It is also shown that for the same value of DM interaction the critical magnetic field of the case D x is larger than that of the case D z.
Entanglement is a fundamental feature of the quantum mechanics, and it is also a potential valuable resource for quantum information processing. As one of the simplest quantum systems which exhibit rich entanglement features, the Heisenberg spin chain is regarded as a natural candidate in the solid state proposals of realizing quantum computing.[1] Considering that thermal fluctuation suppresses quantum effects, the concept of thermal entanglement was introduced to refer to the idea that the effects of temperature should be viewed as the external control in the preparation of entangled states.[2, 3] Up to now, considerable theoretical studies have been done on the thermal entanglement of the Heisenberg spin chains, [4– 14] and moreover the experimental observations of thermal entanglement have also been reported for some magnetic materials.[15– 18]
The diamond Heisenberg spin chain, in which the vertical spin dimers alternate with single spins to form onedimensional lattices composed of diamond-shaped units, is a kind of important and interesting model in the the studies of the Heisenberg spin chains. Since Takano et al. first studied theoretically the ground state of an ideal diamond spin chain in 1996, [19] the theoretical research of the diamond chain has attracted much attention due to rich physical properties as a consequence of the mutual interplay between quantum fluctuations and geometric frustration.[20– 25] In these theoretical works, several modifications of the ideal diamond chain have been proposed, such as the distorted diamond chain, the frustrated diamond chain, and the generalized diamond chain. In 2003, the experimental results reported by Kikuchi et al. showed that the natural mineral azurite Cu3(CO3)2(OH)2 formed by the spin-1/2 Cu2+ ions can be regarded as an actual material for a diamond chain model.[26] Later on, the 1/3 magnetization plateau in the azurite Cu3(CO3)2(OH)2 was observed experimentally.[27, 28] Since then, the physics properties of the azurite Cu3(CO3)2(OH)2, as diamond chain compound, have been investigated on the experimental side with considerable interest.[29, 30] Kikuchi et al. discussed the magnetic anisotropy observed in the magnetization results of azurite, and proposed that the most plausible origin of the magnetic anisotropy is the Dzyaloshinskii– Moriya (DM) interaction since there is no point symmetry in the azurite and the single-ion anisotropy vanishes in spin-1/2 Cu2+ magnetic systems.[27, 28] Additionally, Rule et al. also analyzed the important influence of DM interaction on the ordered magnetic moment structure of the azurite.[30]
We note that the rigorous theoretical treatment of geo-metrically frustrated quantum Heisenberg diamond chains is a very difficult task due to a non-commutability of spin operators involved in these models. To overcome the mathematical difficulties, a novel class of the simplified versions was proposed.[31– 33] In this simplified model called the geometrically frustrated Ising– Heisenberg diamond chain, the Ising spins locate at the nodal sites and the Heisenberg spin dimers are on the interstitial decorating sites of the diamond chain (see Fig. 1). The ground-state phase diagram, the magnetization, the susceptibility, and the thermodynamics of the Ising– Heisenberg diamond chains have already been theoretically examined.[34– 38] Furthermore, the thermal entanglement properties of several kinds of Ising– Heisenberg diamond models, such as spin-1/2 generalized symmetrical Ising– Heisenberg diamond chain, [39] Ising– XXZ diamond chain, [40] Ising– XYZ diamond chain, [41] and the mixed spin-1/2 and spin-1 Ising– Heisenberg diamond chain, [42] have been investigated recently.
The aforementioned DM interaction, which arises from spin– orbit coupling and describes the super-exchange between the interacting spins, was first introduced as anisotropic antisymmetric exchange interactions to explain weak ferromagnetism of the antiferromagnetic crystals.[43, 44] Some antiferromagnetic materials described by DM interaction exhibit unusual and interesting magnetic properties due to quantum fluctuation in the presence of an applied magnetic field. Additionally, it has been found that the DM interaction plays a significant role in the degree of the entanglement of the Heisenberg quantum spin systems.[45– 48] It was found that DM interaction may increase the critical temperature for a two-qubit XX spin chain, [45] and may excite the entanglement and teleportation fidelity for a two-qubit XXX spin chain.[46] It was also shown that the entanglement can be efficiently controlled by DM interaction parameter for the two-qubit XXZ spin model.[47] Recently, the mutual effect of DM interaction and transverse magnetic field on the thermal entanglement for an infinite one-dimensional spin-1/2 XX model has been studied.[48] Motivated by the importance of DM interaction in actual materials such as the azurite Cu3(CO3)2(OH)2, in this paper we will focus on the effect of DM interaction between Heisenberg spins in the dimer on the thermal entanglement of a spin-1/2 Ising– Heisenberg diamond chain. The effects of DM interaction will be discussed according to two different directions of the D vector of DM interaction, respectively. In one case it is assumed that the D vector is perpendicular to both the Heisenberg spin dimer bond and to the chain (i.e., D = Dzez), and the other it is assumed that the D vector is along the direction of the Heisenberg dimer bond (i.e., D = Dxex). We will calculate the concurrence as a measure of Heisenberg spin dimer entanglement. According to the argument of Ananikian et al., [39] each Heisenberg spin dimer interacts with its neighboring dimer through the classical Ising-type interaction, then the states of two adjacent dimers become disentangled. Thus, the calculation of the concurrence can be performed for each Heisenberg spin dimer separately. The concurrence will be constructed for different values of exchange interactions, DM interaction, external magnetic field, and temperature. The critical temperatures and the critical magnetic fields via different DM interaction and exchange interactions will also be obtained, respectively. It will be shown that different DM interaction parameters (Dz and Dx) have remarkably different influences on the entanglement near zero temperature and the critical temperature and magnetic field.
We consider a spin-1/2 Ising– Heisenberg diamond chain model with DM interaction in the presence of an external magnetic field. The model consists of the nodal Ising spins alternating with vertical Heisenberg spin dimers (see Fig. 1). Let us write the total Hamiltonian of the model as a sum over cluster Hamiltonian 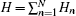
 |
Here, Sn denotes the Heisenberg spin-1/2 operator, and 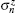
Here, we calculate the concurrence C as a measure of entanglement between Heisenberg spins in the dimer. The concurrence is defined as[49, 50]
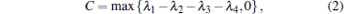 |
where the quantities λ i are the square roots of the eigenvalues of the operator
 |
in descending order (ρ S12 is the reduced density matrix of the Heisenberg spin dimer and 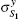
In this section, we assume that the D vector of DM interaction in Hamiltonian (1) is along the z axis, i.e., D = Dzez. As mentioned above, the states of neighboring Heisenberg spin dimers are disentangled due to a classical character of the coupling between them via the Ising spin.[39] Thus, we can calculate the concurrence for each of the dimers individually. We consider the n-th cluster consisting of Heisenberg spin dimer (Sn1 and Sn2) and two Ising spins (σ n and σ n+ 1), and would like to emphasize that each Ising spin belongs simultaneously to two clusters. Then, the sixteen eigenvalues of the n-th cluster Hamiltonian Hn(1) can be given as

where

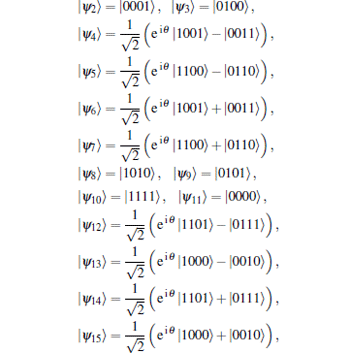
where θ = arctan (J0/DZ). It is noted that here the sequence of the standard basis vectors of the Hilbert space associated with the n-th cluster is defined as {Sn1, σ n+ 1, Sn2, σ n}.
The density matrix ρ n describing the n-th cluster state at temperature T is written as
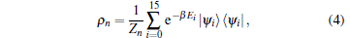 |
with the partition function Zn
 |
We construct the reduced density matrix ρ S12 describing the Heisenberg spin dimer {Sn1, Sn2} by tracing out two Ising spins {σ n+ 1, σ n} in the n-th cluster. In the basis vectors {| 00〉 , | 01〉 , | 10〉 , | 11〉 }, the reduced density matrix ρ S12 can be given by
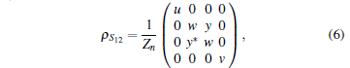 |
where

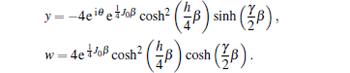
The square roots of the four eigenvalues of the operator ρ defined in Eq. (3) are calculated
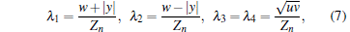 |
so the concurrence as a measure of Heisenberg spin dimer entanglement is given by
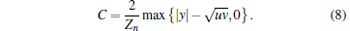 |
We can discuss the effects of DM interaction on the thermal entanglement of the Heisenberg spin dimer by calculating the concurrence (8). Firstly, we consider the case without the magnetic field (i.e., h = 0). In Fig. 2, the variations of concurrence C with the temperature T for different values of Dz are plotted in three different cases (i.e., J − J0 < 0, J − J0 = 0, and J − J0 > 0). Disregarding the DM interaction (i.e., letting Dz = 0), one can obtain results presented by the black solid lines, which are consistent with the results of the previous literature.[39] For the case with J0 = 1 and J = 0.5 (see Fig. 2 (a)), the concurrence C is equal to 1 at zero temperature, monotonically decreases with temperature increasing and reaches zero at the critical temperature Tc corresponding to the vanishing of entanglement. Considering the effect of DM interaction, it is found that the critical temperature Tc increases with | Dz| . For instance, Tc = 0.867, 0.887, 0.941, 1.022, and 1.123, for Dz = 0, 0.25, 0.5, 0.75 and 1.0, respectively. It is also seen that at a fixed temperature (lower than the critical temperature) the concurrence value increases with the DM interaction. The variation of Tc with Dz is shown in Fig. 3, where the black dotted line corresponds to the case with J0 = 1 and J = 0.5. It is concluded that the DM interaction favors the formation of thermal entanglement. This consequence is due to the fact that DM interaction induces the quantum correlation between two Heisenberg spins in the dimer, when the DM interaction is turned on, the low-lying excited states tend to the more correlated.[48]
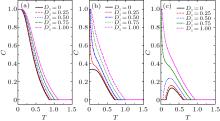 | Fig. 2. The concurrence C versus the temperature T for different values of Dz with h = 0, J0 = 1, and (a) J = 0.5; (b) J = 1; (c) J = 1.1. |
Figure 2 (b) shows the case with J0 = 1 and J = 1. When Dz = 0, the concurrence C starts from 1/3 other than 1 at T = 0, and then with temperature increasing it gradually deceases to zero at the critical temperature Tc = 0.693.[39] When the DM interaction is considered, the concurrence C near zero temperature(e.g., T = 0.005) increases with | Dz| , and gradually reaches its maximum values of 1. The variation of the concurrence C with Dz at T = 0.005 is shown in Fig. 4, where the red dotted line corresponds to the case with J0 = 1 and J = 1. In this case, the maximum entangled state with C = 1 appears when the DM interaction parameter | Dz| is larger than 0.4. In Fig. 3, it is shown that the critical temperature Tc (red dashed-line) also increases with | Dz| , but Tc of the case with J = 1 is smaller than that of the case with J = 0.5 for the same value of the DM interaction parameter Dz.
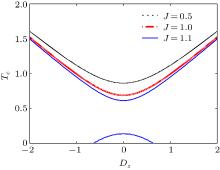 | Fig. 3. The dependence of the critical temperature Tc on Dz for different values of J with h = 0 and J0 = 1. |
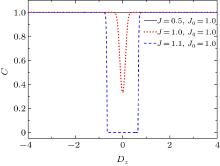 | Fig. 4. The dependence of the concurrence C at T = 0.005 on Dz for different values of J with h = 0 and J0 = 1. |
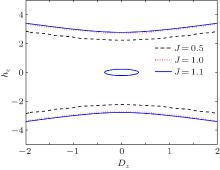
The third case (J − J0 > 0, e.g., J0 = 1 and J = 1.1) is plotted in Fig. 2 (c). In the case of Dz = 0, the Heisenberg spin dimer is not entangled (i.e., the concurrence C = 0) at T = 0. By increasing the temperature from zero, the Heisenberg spin dimer remains unentangled up to the first critical temperature Tc1 = 0.145. As soon as the temperature increases from Tc1, the concurrence C > 0 (i.e., the thermal entanglement regains, that is so-called entanglement revival) and takes a maximum value and then decreases and reaches zero at the second critical temperature Tc2 = 0.617. The existence of the first critical temperature arises from mixing the entangled excited states with the unentangled ground state due to thermal fluctuations, while sufficiently large thermal fluctuations will destroy all quantum correlations so that the second critical temperature occurs. It is observed that with | Dz| increasing, Tc1 gradually decreases to zero, while Tc2 increases. Thus, the width of the temperature interval within which the Heisenberg spin dimer becomes entangled (i.e., the concurrence C > 0) gets larger by increasing | Dz| . As a result, different from the first two cases (J = 0.5 and J = 1), there are two critical temperature lines for the case with J0 = 1 and J = 1.1 in Fig. 3 (shown by two blue solid lines). Further, from blue solid lines in Fig. 3 it is found that if | Dz| is larger than 0.663, the DM interaction can induce the entanglement at T = 0. In fact, at zero temperature, when 

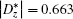
Now, we proceed to study the role of the magnetic field h on the thermal entanglement with the DM interaction Dz. The variations of concurrence C with the magnetic field h for different values of Dz at temperature T = 0.1 are plotted in Fig. 5. Figure 5 (a) shows the case with J − J0 < 0 (here, J0 = 1 and J = 0.5). With | h| increasing, the concurrence C gradually decreases to zero, and moreover the critical magnetic field | hc| corresponding to the vanishing of entanglement increases with | Dz| . For instance, | hc| = 2.25, 2.40, and 2.81, for Dz = 0.5, 1.0, and 2.0, respectively. Here, it is assumed that C with the value less than 10− 3 corresponds to the entanglement disappearing. The dependence of the critical magnetic field hc on Dz is shown in Fig. 6, in which the black dashed-line corresponds to the case with J0 = 1 and J = 0.5.
The case with J0 = 1 and J = 1 is shown in Fig. 5 (b). When Dz = 0, with increasing the magnetic field h the concurrence C firstly increases from 0.333 to a maximum 0.493, and then gradually vanishes. It is found that this maximum of the concurrence C increases with | Dz| up to 1. For instance, the maximums of C are 0.639, 0.887, and 0.998 for Dz = 0.5, 1.0, and 2.0, respectively. Likewise, the critical magnetic field | hc| also increases with | Dz| , but | hc| of the case with J = 1 (also see red dotted line in Fig. 6) is higher than that of the case with J = 0.5 for the same value of the DM interaction parameter Dz.
 | Fig. 5. The concurrence C versus the magnetic field h for different values of Dz with T = 0.1, J0 = 1, and (a) J = 0.5; (b) J = 1; (c) J = 1.1. |
Figure 5 (c) shows the case with J0 = 1 and J = 1.1. In the absence of the DM interaction Dz and the magnetic field h, the concurrence C is zero and Heisenberg spin dimer is unentangled. By increasing | h| from zero, Heisenberg spin dimer still keeps unentangled up to the first critical magnetic field | hc1| = 0.23. When the magnetic field increases from | hc1| , the thermal entanglement(at T = 0.1) revives, and the concurrence C takes a maximum value 0.264 at | h| = 1.20, and then gradually deceases to zero at the second critical magnetic field | hc2| = 2.78. As mentioned above, when Dz = 0 and h = 0, the ground state contains twofold degenerate states | ψ 8〉 and | ψ 9〉 , which are unentangled states. At T = 0.1, with increasing the magnetic field due to admixture of entangled excited states into the mix state, the thermal entanglement regains at the first critical magnetic field | hc1| . The existence of the second critical magnetic field is completely natural, since sufficiently large magnetic field will induce the ground state to be factorable state | ψ 10〉 = | 1111〉 or | ψ 11〉 = | 0000〉 . It is seen that with | Dz| increasing, | hc1| gradually decreases to zero, while | hc2| increases. Thus, for the case with J0 = 1 and J = 1.1, distinct from the first two cases with J = 0.5 and J = 1, the dependence of the critical magnetic field hc on the DM interaction parameter Dz is presented by three blue solid lines in Fig. 6.
In this section we shall study the case that the D vector of DM interaction in the Hamiltonian (1) is along the x axis, i.e., D = Dxex. In principle, the problem of 4-qubit spin models can be solved analytically. However, for the case with the D vector along the x axis the analytical expressions of eigenfunctions and the corresponding eigenvalues of the Hamiltonian (1) are too complex to be compactly given. Thus, in order to obtain explicit physical results, we resort to a numerical calculation method based on the standard process given above.
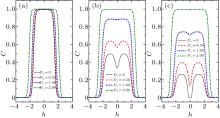
First, we shall start with discussion of the thermal entanglement in the absence of a magnetic field(i.e., h = 0). Figure 7 shows the variations of concurrence C with the temperature T for different values of Dx according to three different cases, i.e., J − J0 < 0, J − J0 = 0, and J − J0 > 0. For the case with J0 = 1 and J = 0.5 (see Fig. 7 (a)), due to the effect of the DM interaction Dx, the maximum of the concurrence C is not located at zero temperature any more, but shifts to a finite T value, and moreover is smaller than 1. For instance, the maximum of the concurrence C is 0.964 at T = 0.115 for Dx = 1.0. This non-monotonic variation of C with T in the case with the D vector along the x axis is obviously different from the case with the D vector along the z axis. For the cases with J − J0 = 0 and J − J0 > 0, the concurrence C increases with Dx, and the non-monotonic variation of C with T is also observed (see Figs. 7 (b) and 7 (c)).
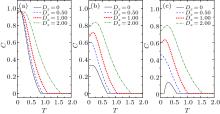 | Fig. 7. The concurrence C versus the temperature T for different values of Dx with h = 0, J0 = 1, and (a) J = 0.5; (b) J = 1; (c) J = 1.1. |
After the concurrence reaches the maximum, it decreases gradually with temperature increasing and vanishes at the critical temperature Tc. The dependence of the critical temperature Tc on Dx for different values of J is plotted in Fig. 8. Compared with the case Dz (see Fig. 3), the effect of Dx on the thermal entanglement has a distinct property in the case with J − J0 > 0 (see blue solid line in Fig. 8), in which the DM interaction Dx can induce the entanglement characterized by a nonzero concurrence near zero temperature. Specifically, for very small | Dx| , there exist three critical temperature values in the case with J0 = 1 and J = 1.1.
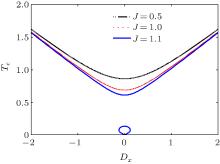 | Fig. 8. The dependence of the critical temperature Tc on Dx for different values of J with h = 0 and J0 = 1. |
Additionally, the dependence of the concurrence C on Dx for different values of J near zero temperature (e.g., T = 0.01) is shown in Fig. 9. For the case with J0 = 1 and J = 0.5, with | Dx| increasing, the concurrence C firstly decreases from 1 to a minimum of 0.940 at | Dx| = 1.29, and then gradually increases, while for the case with J − J0 ≥ 0, it is observed that the concurrence C increases with | Dx| . The results given by Fig. 9 (for the DM interaction Dx) are obviously different from those of the case Dz (see Fig. 4).
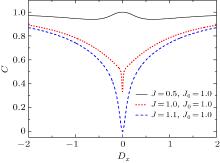 | Fig. 9. The dependence of the concurrence C at T = 0.01 on Dx for different values of J with h = 0 and J0 = 1. |
Now, we concentrate on the thermal entanglement in the presence of a magnetic field. The variations of concurrence C (at T = 0.1) with the magnetic field h for different values of Dx are plotted in Fig. 10. Figure 10 (a) shows the case with J − J0 < 0 (here, J0 = 1 and J = 0.5). Due to the effect of Dx, with | h| increasing, the concurrence C firstly increases to a maximum, and then gradually decreases to zero. Likewise, the critical magnetic field | hc| increases with | Dx| , and the variation of hc with Dx is also shown in Fig. 11 (here, the black dashed line corresponds to the case with J0 = 1 and J = 0.5). It is found that for the same value of the DM interaction the critical magnetic field | hc| of the case Dx is higher than that of the case Dz.
Figures 10 (b) and 10 (c) show the cases with J − J0 = 0 and J − J0 > 0, respectively. Compared with the case Dz (see Figs. 5 (b) and 5 (c)), the concurrence C shows a different variation tendency in Figs. 10 (b) and 10 (c). At T = 0.1, for the case with J − J0 > 0, there exist two critical magnetic fields | hc1| and | hc2| (| hc1| < | hc2| ) without the DM interaction (see black solid line in Fig. 10 (c)). With | Dx| increasing, the first critical magnetic field | hc1| gradually decreases, while the second critical magnetic field | hc2| increases (see blue solid lines in Fig. 11). Noted that for the same value of the DM interaction, | hc1| of the case Dx is smaller than that of the case Dz, but | hc2| of the case Dx is higher than that of the case Dz.
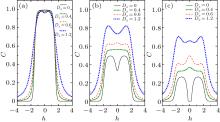 | Fig. 10. The concurrence C versus the magnetic field h for different values of Dx with T = 0.1, J0 = 1, and (a) J = 0.5; (b) J = 1; (c) J = 1.1. |
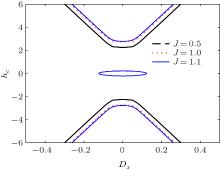 | Fig. 11. The dependence of the critical magnetic field hc on Dx for different values of J with J0 = 1 and T = 0.1. (Here, it is assumed that C with the value less than 10− 3 corresponds to the entanglement disappearing). |
In summary, the thermal entanglement of a spin-1/2 Ising– Heisenberg diamond chain with the DM interaction between Heisenberg spins has been investigated. As is well known, the DM interaction plays a significant role in the degree of the entanglement of the Heisenberg quantum spin systems. In this paper, we are concerned with the effects of different DM interaction parameters, relating to variations of direction and amplitude of the D vector, on the thermal entanglement of the Heisenberg spin dimer. Two cases, i.e., z-component DM interaction parameter (Dz) and x-component DM interaction parameter (Dx), are discussed respectively. In the absence/presence of magnetic field, the concurrence as a measure of spin dimer entanglement is calculated. The variations of the concurrence with different values of exchange interactions, DM interaction, external magnetic field, and temperature are shown. The critical temperatures and the critical magnetic fields via different DM interaction parameters and exchange interactions are also obtained, respectively. It is found that the DM interaction favors the formation of thermal entanglement. Furthermore, it is shown that different DM interaction parameters (Dz and Dx) have remarkably different influences on the entanglement near zero temperature and the critical temperature and magnetic field.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|