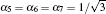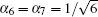In recent years, quantum entanglement, which plays a very important role in quantum information processing, has attracted extensive attention. However, due to the inevitable interaction of a realistic system with its surrounding environments, the entanglement degrades with time and even completely disappears in a finite time, which is termed as the entanglement sudden death.^{[1– 4]} Therefore, it is important to protect entanglement as a major resource for quantum information and quantum computation.

So far, there has been much literature on the dynamics of a bipartite atomic system under different kinds of environments including independent and common ones.^{[5– 9]} It is observed that in the non-Markovian reservoirs, the entanglement sudden birth appearing after complete disappearance depends on the initial state of the system.^{[10, 11]} Besides, in the thermal and vacuum environments, taking into account the two atoms close together, due to the presence of collective damping and dipole– dipole interaction, Tahira et al.^{[12– 16]} found the revival of entanglement and the oscillatory behavior. In the same model, Berrada et al.^[17] studied the quantum correlation of each atom with its environment in terms of the critical distance. As is well known, the multipartite entanglement is significant for quantum tasks in many areas of physics, such as quantum information and communication theory.^[18] Because of its complexity and lack of good measures, many aspects of the multipartite entanglement are not well studied. Recently, the dynamics of three qubits was investigated with the dipole– dipole interactions and the atom– cavity couplings considered.^{[19– 24]} An et al.^[25] proposed a model of three atoms coupled to a common environment and investigated the tripartite entanglement via the lower bound of concurrence.

In this paper, we investigate the entanglement dynamics of a three-qubit atomic system interacting with a multimode vacuum field. When the atoms are initially prepared in W-like states and arranged in two different geometries (an equilateral triangle and a line), we study the influences of the distance between the atoms and the initial condition on the tripartite entanglement by using the lower bound of concurrence and the tripartite negativity.^{[26– 28]} Considering the equality of all the pairwise distances, we can obtain the analytical result via the Laplace transform. For the initially entangled states, the optimal interatomic distance that minimizes the collective damping is exactly the one that maximizes the tripartite entanglement. While for some initially separable states, this is not the case. In the short time limit, we can see the oscillatory (or exponential) behavior of the tripartite entanglement at very small (or large) distances. In the long time limit, the tripartite entanglement tends to a stationary value which is dependent on the interatomic distance and the initial condition. Moreover, contrary to the previous studies, we investigate the situation with different distances between the atoms. The paper is organized as follows. In Section 2, we present the model for our system, where the lower bound of concurrence and the tripartite negativity play important parts in the measure of the three-qubit entanglement. In Section 3, we study some important factors like the interatomic distance and different initial conditions which can influence the entanglement in the tripartite system. In Section 4, we summarize our work. In the Appendix, we obtain the exact solutions for W states.

We consider a quantum system in which three identical two-level atoms are coupled to a quantized multimode electromagnetic field. The atoms are close to each other, the transition dipole moment, the collective damping, and the dipole– dipole interaction cannot be ignored. In the interaction picture, the Hamiltonian of the system can be written as (ħ = 1)

where ω _i and ω _k are the transition frequency of the atoms and the frequency of the field mode, respectively; d_i is the atomic transition dipole moment; is the raising (lowering) operator of the i-th atom; and is the creation (annihilation) operator of mode ks of the field with k the wave vector and s the index of polarization. The coupling constant can be given by

where ε ₀ is the vacuum permittivity, V is the quantization volume, ê _ks is the electric field polarization vector, and r_i is the position of atom i.

According to the rotating wave approximation and a Markovian approximation, the Lehmberg– Agarwal master equation of the three atoms inside their local vacuum environments can be written as

where is the i-th atom’ s energy operator, | e〉 _i (| g〉 _i) is the excited (ground) state of the atoms, and γ _ij ≡ γ (i = j) is the spontaneous decay rate. Moreover, γ _ij and Ω _ij (i ≠ j), depending on the distance between different atoms i and j, describe the collective damping and the dipole– dipole interaction, which can be respectively given by

where k = 2π /λ , λ is the resonant wavelength of the atoms, r_ij = | r_i − r_j| is the distance between the two atoms, and θ is the angle between the atomic transition dipole moments and the orientation of the interatomic axis. Furthermore, the results in the presence of collective damping and dipole– dipole interaction are complicated depending on different spatial configurations through the atomic transition dipole moment d_i and the interatomic distance r_ij. To account for this fact, we shall distinguish among three cases about the pairwise distances, that is, all the pairwise distances are equal (r₁₂ = r₁₃ = r₂₃, case 1); two of the three distances are equal but different from the third one (r_ij = r_kl ≠ r_mn, case 2); all the pairwise distances are different (r₁₂ ≠ r₁₃ ≠ r₂₃ ≠ r₁₂, case 3).

Considering the initial state of the three-qubit atomic system^[29] in the form

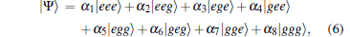where α _i is the probability amplitude with the normalization condition , we can obtain the solutions of the density matrix elements by solving the master equation (3) in the basis. Let | 1〉 → | eee〉 , | 2〉 → | eeg〉 , | 3〉 → | ege〉 , | 4〉 → | gee〉 , | 5〉 → | egg〉 , | 6〉 → | geg〉 , | 7〉 → | gge〉 , | 8〉 → | ggg〉 for short.

In the following, we use two well-defined measures of the tripartite entanglement to assess the amount of entanglement analytically: the lower bound of concurrence and the tripartite negativity. First, for three qubits, we adopt the lower bound of concurrence as the measure of entanglement, ^{[21, 22, 24– 27]} which is defined as

where are the eigenvalues listed in descending order of the matrix . Here, ρ * is the complex conjugation of ρ in the basis of three qubits, is one of the six generators of group SO(4) operating on qubits i and j, and is the y Pauli matrix operating on qubit k.

Another entanglement is the tripartite negativity, ^{[20, 28]} whose expression is given as

where N^{i− jk} = 2max{0, − λ _min}, λ _min are the lowest eigenvalues of the partially transposed matrix ρ ^T_i of ρ with respect to subsystem i, 〈 l_i, m_j, n_k | ρ ^T_i| o_i, p_j, q_k〉 = 〈 o_i, m_j, n_k | ρ | l_i, p_j, q_k〉 (l, m, n, o, p, q = e, g).

We suppose that the atoms are prepared in the W state at the initial time and emphasize that the choice of the present initial state is made only for clarity and the analysis is general. The W-like initial state is of the form

Let us consider the situation of case 1 and θ = 5π /6 which corresponds to the most symmetric configuration. That is to say, the atoms sit on the vertices of an equilateral triangle within the vacuum environment. Here, the nonzero solutions of the density matrix elements (see Appendix A) can be evaluated from the master equation (3) by means of the Laplace transform. Given the density matrix elements, we can now calculate the lower bound of concurrence and the tripartite negativity, which are respectively given by

First, to explore the dependence of the dynamical behaviors of the tripartite entanglement on the interatomic distance, we plot, in the short time period, the lower bound of concurrence and the tripartite negativity as a function of the distance r₁₂/λ in Fig. 1. For the atoms that are initially prepared in the maximally entangled states , the explicit expressions of the lower bound of concurrence and the tripartite negativity can be respectively given as follows:

From Eqs. (12) and (13), we can immediately conclude that C₃ and N₃ are primarily controlled through the collective damping, and are independent of the dipole– dipole interaction.

Figure 1 shows that the time evolutions of C₃ and N₃ behave similarly regarding the interatomic distance. Interestingly, during the same time period, there is one maximum of the entanglement at a specific distance, and we will discuss this in detail in the following. In Fig. 2(a), we show the variation of C₃ and N₃ with the distance for different values of the time γ t. It is worth noticing that for each moment, at the optimal distance r₁₂ = 0.814λ , C₃ and N₃ reach their maximal values, and the entanglement of Fig. 1 also shows the slowest decay. At the same distance r₁₂ = 0.814λ , the collective damping γ ₁₂ = − 0.1079γ reaches its minimal value, as can be seen from Fig. 2(c). This indicates that the entanglement and the collective damping are very sensitive to the distance. Moreover, due to the spontaneous emission, for the same distance, C₃ and N₃ decrease monotonously down to zero with γ t increasing in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Contour plots of two different measures of tripartite entanglement versus r12/λ and γ t with : (a) C3, (b) N3.

However, comparing the two graphs of Fig. 1, we find that for the same distance, C₃ decays slower compared with N₃. To show this, we plot in Fig. 2(b) the time variation of the tripartite entanglement for different values of the collective damping γ ₁₂. As observed from Fig. 2(b), γ ₁₂ increases from γ ₁₂ = − 0.1079γ up to γ ₁₂ = γ , which speeds up the atoms’ disentangling process. Furthermore, it is clear by inspection of Eqs. (12) and (13) that for whatever γ ₁₂, the death time of N₃ can be much longer than that of C₃.

Next, to highlight the distinct effect of the initial condition of the system on the entanglement among the three atoms, we plot, at a fixed moment of time (γ t = 1), the difference of the entanglement with the interatomic distance r₁₂/λ for the initially entangled states from that of the initially separable states in Figs. 3(a) and 3(b). For the initially entangled states, the choice of the different values of the probabilities α _i does not alter the optimal distance for the maximal entanglement in comparison to some initially separable states. Moreover, in the situation of equal probabilities α _i (i.e., α ₅ = α ₆ = α ₇), the entanglement depends crucially on the collective damping, while in the situation of unequal probabilities α _i (i.e., α _i = α _j ≠ α _k or α _i ≠ α _j ≠ α _k), the entanglement is profoundly affected by the dipole– dipole interaction. From Figs. 2(a) and 3, we note also that when r₁₂ < 0.37 λ , the dipole– dipole interaction can induce the oscillatory behavior of the entanglement. Meanwhile, due to the rapid energy exchange, the rapid oscillatory behavior of the entanglement happens at weak dipole– dipole interaction. This fact explains the absence of the oscillatory behavior in Fig. 4(a) when , as opposed to the presence of the oscillatory behavior in Fig. 4(b) when and . Considering the non-existence of the dipole– dipole interaction and r₁₂ < 0.37 λ , the entanglement of Fig. 4(a) will quickly disappear in a finite time. On the contrary, the entanglement of Fig. 4(b) will tend to a stationary value in the long time limit. For shorter the atomic distance (i.e., γ ₁₂ ≈ γ ), from Eq. (10), the long-term behavior of the entanglement is derived as

From the above equation, it is obvious that the stationary value of the entanglement is not related to the concrete values of the collective damping and the dipole– dipole interaction. This result may accomplish protecting the entanglement for a sufficiently long time (i.e., it can slow down the degradation of the entanglement). So, with appropriate probabilities α _i, the long-term entanglement can obtain a large value. At relatively large distance r₁₂ (i.e., r₁₂ > 0.37 λ ), there will be a strong resemblance between the presence and absence of the dipole– dipole interaction, namely, the entanglement behaves as the exponential decay. With a further increase in distance r₁₂ (i.e., γ ₁₂≪ γ ), the collective damping and the dipole– dipole interaction decay to zero (see Figs. 2(c) and 3(c)) and the dynamical behaviors of the entanglement behave as that of three independent atoms in a common environment.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) The entanglement versus r12/λ with for various values of γ t, and (b) the entanglement versus γ t with for various values of γ 12. The solid (blue, red, green) line is for C3, and the dashed (blue, red, green) line is for N3. (c) The γ 12/γ versus r12/λ with θ = 5π /6.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The C3 versus r12/λ with γ t = 1 and (a) initially entangled states or (b) initially separable states. (c) The Ω 12/γ versus r12/λ with θ = 5π /6.

For the initial entanglement, from Eq. (10), we can readily calculate

To estimate the difference between the initial entanglement and the stationary entanglement , we use Eqs. (14) and (15), and plot the entanglement versus for both initially entangled and separable states in Fig. 5(a). Note that behaves as a non-monotonic increasing (decreasing) function of . In other words, in the course of increasing , is first increasing (decreasing) too, but after reaching a maximum (minimum), it will be decreasing down to zero (increasing to a certain value equal to (8/27)^1/2). Furthermore, there is a competition between and . For the initially entangled (separable) states, exceeds when , while exceeds when and .

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. A 3D view of C3 versus r12/λ and γ t with (a) or (b) , .

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (a) The C3 versus for various initial conditions. The solid (red, black) line is for , and the dashed (red, black) line is for . The C3 versus γ t for various values of rij/λ and (b) or (c) , .

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. The C3 versus γ t with (a) r12 = r13 = r23 = 0.05λ , θ = 5π /6, (b) r12 = r13 = r23/2 = 0.05λ , θ = π /2, or (c) r12 = r13/2 = r23/3 = 0.05λ , θ = π /2. The black (solid, dashed) line is for , and the red (solid, dashed) line is for , .

Finally, we consider either case 2 or case 3 with θ = π /2, namely, the atomic dipole moments are parallel to each other and are polarized in the direction perpendicular to the interatomic axis. When only two among r₁₂, r₁₃, r₂₃ are equal (i.e., case 2) or when the r_ij are all different (i.e., case 3), as the analytical solutions of the density matrix elements are very complicated, only the numerical solutions can be used. The plots of C₃ for the three cases are shown in Figs. 5(b) and 5(c). For the interacting atoms, the entanglement of the three cases with different pairwise distances presents similar responses. More concretely, it is understandable that the entanglement can always be taken as being made up of the contributions of the collective damping and the dipole– dipole interaction associated with the interatomic distance. Thus, we respectively study the effects of the collective damping and the dipole– dipole interaction. From Fig. 6, we notice that when , if there is the collective damping without the dipole– dipole interaction (i.e., γ _ij ≠ 0 (i ≠ j) and Ω _ij = 0 (i ≠ j)), the entanglement degrades exponentially with time. When and , the entanglement quickly decreases down to zero and then increases to a stationary value. On the other hand, if there is the dipole– dipole interaction without the collective damping (i.e., γ _ij = 0 (i ≠ j) and Ω _ij ≠ 0 (i ≠ j)), the entanglement exhibits damped oscillation, except when the probabilities α _i and the distances r_ij are all equal.

We have investigated the entanglement dynamics for a system composed of three atoms coupled with their common vacuum environment. If the interatomic distances are all equal, we can obtain the explicit solutions of the density matrix elements. There is an interesting feature in the system, an optimal distance emerges wherein the entanglement of the three atoms is at a maximum and the collective damping is at a minimum. For larger distances, the entanglement exhibits the exponential decay. For shorter distances, by adjusting the initial conditions, the oscillatory behavior of the short time entanglement occurs, whereas in the long time limit, the tripartite entanglement tends to a stationary value, and this provides a possible method for long time maintenance of the entanglement. If two among the three distances are equal or the distances are all different, the behavior of C₃ is similar to that of the cases with all equal distances.