Since the rapid experimental development in macroscopic solid state physics, the superconducting circuits based on the Josephson junction have become a hot topic of theoretical and experimental research.^{[1– 15]} The superconducting circuits exhibit many interesting properties that do not appear in natural atoms and have been regarded as a promising candidate in quantum information and quantum computation.^{[6, 7]} Quantum information processing in the superconducting qubit system is performed at very low temperatures, so the energy relaxation is expected to vanish due to the density decreasing exponentially with decreasing temperature.^{[6, 7]} It has been experimentally verified that the superconducting circuits display macroscopic quantum coherence and may be used to realize the conditional two-qubit gate.^[8] Several methods^[12] have been developed to couple pairs of qubits with a common data bus selectively.

In recent years, there has been considerable interest in the study of quantum correlations in quantum information processing.^[16] It is well known that entanglement is a special kind of quantum correlation and plays an important role in the current development of quantum information science.^{[16, 17]} It has been proved both theoretically^{[14, 18, 19]} and experimentally^{[20, 21]} that other nonclassical correlation, namely, quantum discord, ^[22] is able to be responsible for the computational speedup for some quantum tasks. Quantum discord, first introduced in Ref.  [22], is defined as the difference between the quantum mutual information and the classical correlation and is nonzero even for separate mixed states. It is recently reported that quantum discord may be quantified in a geometric way.^{[23, 24]} The measure of geometric quantum discord has been demonstrated to be the necessary resource for quantum remote state preparation.^[22]

In the present paper, we study the effects of the dynamical decoupling pulses on the geometric discord of a system containing two uncoupled qubits interacting with their independent data buses.^[25] It is discovered that the geometric quantum discord and entanglement can be enhanced by applying a train of π -phase pulses. Furthermore, we investigate how to control the exchange of the quantum information flows between two superconducting qubits and their independent data buses by using the change of trace distance of the two superconducting qubits, and find that the decoupling pulses can control the quantum information to flow back from the data buses to the two superconducting-qubit subsystem effectively.

We consider two superconducting flux qubits interacting with their own data buses. The data bus can be realized simply as an LC circuit, and the interaction between a single superconducting flux qubit and an LC circuit has been experimentally realized.^[10] The qubit circuit is composed of a superconducting loop with three Josephson junctions and the two larger ones have equal Josephson energies E_J1 = E_J2 = E_J and capacitances C_J1 = C_J2 = C_J, while for the third junction, E_J3 = γ E_J and C_J3 = γ C_J, with γ < 1. The Hamiltonian of the superconducting qubit is ^[12]

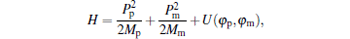
where M_p = 2C_J(Φ ₀/2π )² and M_m = M_p(1 + 2γ ), which correspond to effective momenta P_p and P_m, Φ ₀ is the flux quantum, and U(φ _p, φ _m) = 2E_J(1 − cosφ _pcosφ _m) + γ E_J[1 − cos(2π f + 2φ _m)] is the effective potential. Here φ _p = (φ ₁ + φ ₂)/2, φ _m = (φ ₁ − φ ₂)/2, φ ₁ and φ ₂ are the phase drops across the two larger junctions, and f = Φ _e/Φ ₀ is the reduced magnetic flux, with Φ _e being the externally applied flux and Φ ₀ the flux. The LC circuit interacts with its qubit through its mutual inductance M. In the rotating-wave approximation, the Hamiltonian of two superconducting qubits independently interacting with their data buses can be written as^[12]

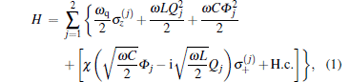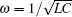
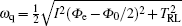
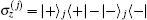
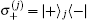
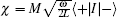
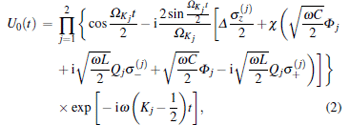where we have set ħ = 1, Φ _e is the bias flux, C is the capacitance, and L is the self-inductance. The magnetic flux Φ _j through the LC circuit and the charge operators Q_j obey the commutation relation [Q_j, Φ _k] = iδ _jk. Here and are the frequencies of the data bus and the qubit, respectively. The parameter T_RL denotes the tunnel coupling between the two potential wells of the qubit, ^[1] and I is the qubit loop current. The operators and are defined as , , and , where | + 〉 _j and | − 〉 _j are the excited and the ground states of the j-th qubit, respectively. The χ is the coupling constant between the qubit and the data bus, which can be written as , here we assume that it is the same for both qubits. The time evolution operator U₀(t) = exp(− iHt) for the two qubits interacting with their data buses is given by

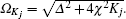
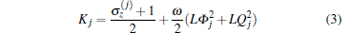where Δ = ω _q − ω and Here

is a conserved quantity with the Hamiltonian, i.e., [K_j, H] = 0 (j = 1, 2).

Now, we consider the system of two superconducting qubits with the π -phase pulses. In general, the control pulse field is presented as

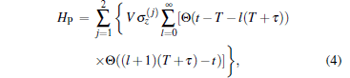where Θ is the step function, T is the time interval between two consecutive pulses, and the amplitude V of the control pulses is π /2τ , meaning that the π -phase pulses are considered in this paper. Therefore, the time evolution operator for the duration τ can be obtained as

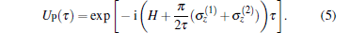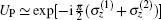
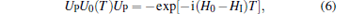For the case in which the pulses are strong enough, i.e., the duration τ → 0, this time evolution operator can be rewritten as , which leads to

where

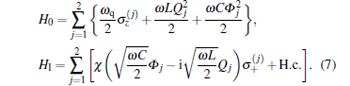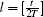
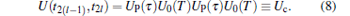In the interval between t_{2(l− 1)} = 2(l − 1)(T + τ ) and t_2l = 2l(T + τ ) (here is a set of integers), the evolution operator for the system is given by

Then, the evolution operator in a period with the pulses is written as

where

We can write the evolution operator at time t = t_2l + t̃ for the system with the the π -phase pulses as

We assume that the superconducting qubits are initially prepared in Bell-like-state cosθ e^iϑ | − 〉 | − 〉 + sinθ | + 〉 | + 〉 , where e^iϑ is the relative phase factor, and the data buses are initially prepared in Fock state | n, n〉 . Then the initial state of the whole system is

By using Eqs.  (11) and (12), in the basis of | + 〉 | + 〉 ,   | + 〉 | − 〉 ,   | − 〉 | + 〉 ,   | − 〉 | − 〉 , we obtain the reduced density matrix of the superconducting qubits by tracing over the data buses

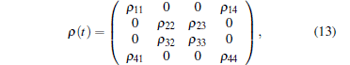where

with

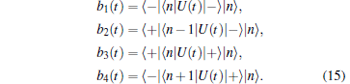Now, we study the influence of the π -phase pulses on the dynamics of geometric discord and entanglement between the two superconducting qubits each interacting with their own data buses. In Ref.  [23], a necessary and sufficient condition for the existence of the nonzero quantum discord has been discussed and a geometric measure of quantum discord has been introduced, and the geometric discord is proven to be the necessary resource^[26] for quantum remote state preparation. The definition of geometric discord is^[23]

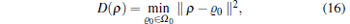where Ω ₀ denotes a set of classical-quantum two-qubit states whose geometric discord is zero and invariant by a measurement^[24] on one of the two qubits in any case, ϱ ₀ is the generic element, and | | A | | ² = Tr(A)² is the square norm in the Hilbert– Schmidt space. For a two-qubit system, the maximum value of geometric discord is 0.5 with the maximal entangled state.^[23] In the Bloch representation, the density matrix ρ for a two-qubit state can be described by^[23]

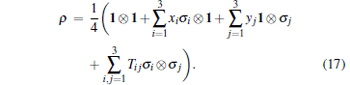Each state ρ is associated with the triple {x, y, T}, in which x_i = Trρ (σ _i ⊗ 1) and y_i = Trρ (1 ⊗ σ _i) are components of the local Bloch vectors, T_ij = Trρ (σ _i ⊗ σ _j) are components of the correlation tensor, and σ _i and σ _j (i, j = 1, 2, 3) are the Pauli matrices. By optimizing the distance between the state ρ and a zero-discord state ϱ ₀, the geometric discord can be written as

where K_max is the maximal eigenvalue of

If the density matrix is in the X-form with ρ ₂₃ = ρ ₃₂ = 0 (ρ _ij is the matrix element of ρ in the standard basis), the above components of the correlation tensors can be derived as^[27]x₁ = x₂ = 0, x₃ = ρ ₁₁ + ρ ₂₂ − ρ ₃₃ − ρ ₄₄, T₁₁ = − T₂₂ = 2ρ ₁₄, T₃₃ = ρ ₁₁ − ρ ₂₂ − ρ ₃₃ + ρ ₄₄, T_ij = 0 (i, j = 1, 2, 3, and i ≠ j), and the geometric discord reads

In order to quantify the entanglement between the superconducting qubits and make a comparison with the quantum discord dynamics, we adopt the measure concurrence which is defined as^[28]

where η _i (i = 1, 2, 3, 4) are the eigenvalues in decreasing order of magnitude of the spin-flipped density matrix operator R = ρ (σ ₂⊗ σ ₂)ρ * (σ ₂⊗ σ ₂), and σ ₂ is the Pauli Y matrix, i.e., . Combining the definition of concurrence with the density matrix ρ (t) of Eq.  (13), we can find the the explicit expression of the concurrence between the superconducting qubits

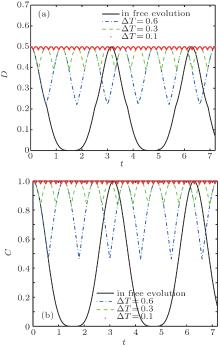
In order to study the influence of the π -phase pulses on the evolution of geometric discord and entanglement between the superconducting qubits, we plot the geometric discord (Fig.  1(a)) and entanglement (Fig.  1(b)) between the superconducting qubits as a function of evolution time t and T with χ = 1, ω = 1, Δ = 0, n = 0, and θ = π /4. It can be seen from Fig.  1 that the π -phase pulses can help recover the geometric discord and entanglement between the superconducting qubits during the evolution.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Quantum discord and entanglement are plotted as a function of time and T with χ = 1, ω = 1, Δ = 0, n = 0, and θ = π /4.

The geometric discord (Fig.  2(a)) and entanglement (Fig.  2(b)) as a function of evolution time t for different T with χ = 1, ω = 1, Δ = 0, θ = π /4, and n = 0 are displayed. We can see from Fig.  2 that the geometric discord and entanglement recover their initial values at time t_2N when Δ = 0 and the variation period of geometric discord and entanglement equals to 2T if the π -phase pulses are applied to the superconducting qubits, which implies that the π -phase pulses can be used to preserve the initial entanglement and control the variation period of geometric discord and entanglement between the two superconducting qubits. Furthermore, it is interesting to note that the π -phase pulses can be used to control the death time intervals of both quantum discord and entanglement as to erase the death time intervals of them, if the pulses’ time interval T is sufficiently short.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Geometric discord and (b) entanglement are plotted as a function of time for different T with χ = 1, ω = 1, Δ = 0, θ = π /4, and n = 0.

In this section, we explore the influence of the π -phase pulses on the exchange information between the superconducting qubits and their own data buses by making use of the trace distance. The trace distance, which can be obtained experimentally by using the quantum-state tomography^[16], has been used to study the influence of the initial correlation between system and environment on the dynamics of the open system^{[29, 30]} and to qualify the non-Markovianity for quantum processes.^{[31, 32]} The trace distance between two states of ρ and ϱ is defined by^[16]

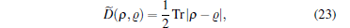where is the positive square root eigenvalue of A^† A. There are several properties of the trace distance, ^[15] such as 0 ≤ D̃ (ρ , ϱ ) ≤ 1, where D̃ (ρ , ϱ ) = 0 means ρ = ϱ and D̃ (ρ , ϱ ) = 1 means that ρ is orthogonal to ϱ , and D̃ (Λ ρ , Λ ϱ ) ≤ D̃ (ρ , ϱ ), where Λ is any positive and trace-preserving quantum operation. In particular, the trace distance preserves under unitary transformations

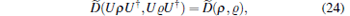which means if we regard the system and its environment as a whole, the trace distance between the reduced system states at time t is never larger than its initial value when the two initial states of the system are the product states with the same environment. In this case, the reduced state ρ (t) is regarded as a completely positive and trace preserving map Λ for its initial state ρ (0) with ρ (t) = Λ ρ (0). Now, we focus on the change of the trace distance of the system, which has been used to describe the transfer of information in a quantum system with the concept of information flows. The change rate of the trace distance of a pair of states is defined by^[32]

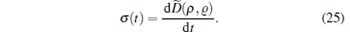For a non-Markovian process, information must flow from the environment to the system for some interval of time, and thus we must have σ (t) > 0 for this time interval. A measure of non-Markovianity is the total amount of information flowing from the environment back to the system, which can be written as ^[32]

where for all time intervals (t_i, t_{i+ 1}), σ is positive and the maximum is taken over all pairs of initial states. Next, we investigate how the π -phase pulses affect the information flows in the superconducting qubits system. For the initial state in this paper with a different relative phase Δ ϑ , the trace distance of the two superconducting qubits at time t can be derived as

where Δ ρ = ρ (θ , ϑ ₂, t) − ρ (θ , ϑ ₁, t) (denoted as Δ ρ = ρ (ϑ ₂) − ρ (ϑ ₁) for simplicity)

The explicit expression for the trace distance of the two superconducting qubits in free evolution with Δ φ = φ ₂ − φ ₁ = π is simply given by

We plot the trace distance D̃ for the two superconducting qubits as a function of Ω t with Δ ϑ = π in free evolution in Fig.  3.

Fig.  3.

	Figure Option ViewDownloadNew Window
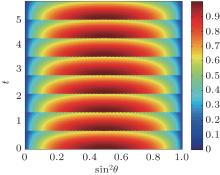	Fig.  3. The trace distance D̃ of two states of superconducting qubits is plotted as a function of (sinθ )2 and t with a train of π -phase pulses having interval time of T = 0.7 for Δ ϑ = π and Δ = 0.

It is quite clear from Fig.  3 that the trace distance recovers its initial value at a certain time point after every π -phase pulse applying to the superconducting qubits, and the corresponding instant information flows back to the subsystem of the two superconducting qubits from the data buses. The result shows that the instant information flows can be controlled by the π -phase pulses.

We investigate how the dynamical decoupling pulses affect the quantum correlations in a superconducting system consisting of two superconducting qubits interacting with their own data buses, and find that the amounts of geometric discord and entanglement of the two-superconducting-qubit subsystem can be improved if we choose the suitable dynamical decoupling pulses. It is important to point out that if the π -phase pulses’ time interval T → 0, the quantum correlations between the superconducting qubits can be protected all the time. Furthermore, the transfer of the quantum information between the two superconducting qubits and their own data buses can be witnessed by means of the change of the trace distance of the two superconducting qubits, and we find that the π -phase pulses can control the quantum information to flow back from the data buses to the two-superconducting-qubit subsystem immediately. The approach adopted here may be extended to improve the implementation of quantum information processing and quantum computation.