†Corresponding author. E-mail: rejojeice@gmail.com
Simultaneous effect of hydrostatic pressure and polaronic mass on the binding energies of the ground and excited states of an on-center hydrogenic impurity confined in a GaAs/GaAlAs spherical quantum dot are theoretically investigated by the variational method within the effective mass approximation. The binding energy is calculated as a function of dot radius and pressure. Our findings proved that the hydrostatic pressure led to the decrease of confined energy and the increase of donor binding energy. Conduction band non-parabolicity and the polaron masses are effective in the donor binding energy which is significant for narrow dots not in the confined energy. The maximum donor binding energy achieved by the polaronic mass in the ground and excited states are 2%–19% for the narrow dots. The confined and donor binding energies approach zero as the dot size approaches infinity.
In the last few decades, the properties of low-dimensional semiconductor systems (LDSS)[1, 2] have drawn great interest amidst the theoretical and applied physicists due to the quantum confinement.[3] The ample of nano fabrication techniques such as molecular beam epitaxy (MBE), [4] metal organic chemical vapor deposition (MOCVD), [5] and self-assembled method have been developed to synthesize the different sizes and shapes of semiconductor quantum dots (QD’ s), [6, 7] quantum wires, [8] and quantum well[9] due to their significant applications in distinct fields. Among these, quasi-zero-dimensional systems (QD) became a hot topic, since the carrier motion is restricted to a narrow region of a few nanometers in dimension and its effects of hydrostatic pressure on QD were studied by many researchers.[10– 19] Peter calculated the ionization energies in external perturbations such as hydrostatic pressure and magnetic field with a parabolic confinement for finite barrier quantum dots.[10] He found that the ionization energy is purely pressure dependent and for smaller dot sizes the hydrostatic pressure dominates. The effects of static electric field and hydrostatic pressure on the donor binding energy and ionization energy for a spherical quantum dot (SQD) with parabolic confinement have been reported.[11] The donor and acceptor binding energy increases with the hydrostatic pressure for any position of the impurity in a SQD.[12] In the low pressure regime, the impurity binding energy grows linearly with pressure and in the high pressure regime the binding energy grows up to a maximum and then decreases in a QD.[13] Xia et al. investigated the hydrostatic pressure effects on the donor binding energy of a hydrogen impurity in an InAs/GaAs self-assembled quantum dot.[14] The linear and nonlinear optical properties of multilayered spherical quantum dots under hydrostatic pressure have also been studied.[15] The effects of electric field, hydrostatic pressure, and temperature on the binding energy in SQD have been reported by Rezaei et al.[16] Prodigious copies are available for the effects of hydrostatic pressure, temperature, and conduction band non-parabolicity on the impurity binding energy in an SQD.[17, 18] Though the effects of hydrostatic pressure, temperature, and polaronic mass on the correlation energies in an SQD[19] have been widely investigated, very few reports explore the effect of polaron mass on donor binding and confined energies. Hence, the present work focuses on analyzing the hydrostatic pressure and polaronic effects in the SQD of the donor binding and confined energies.
In the present work, we consider a GaAs QD embedded in a Ga1− xAlxAs matrix with finite barriers in which the barrier height depends on x. When an electron is introduced into the dot, the total energy of the system is estimated, by assuming SQD potential confinement for the barrier heights.
We consider a single electron in an SQD in the finite barrier model. In the presence of on-center hydrogenic impurity, within the effective mass approximation, the Hamiltonian can be written as
 |
where VD(r, P), ε (P), and m* (P) are the hydrostatic pressure dependent confining potential, the dielectric constant, and the effective mass of the electron at the conduction band minimum respectively, in which the effective mass of the electron is 0.067m0 for GaAs, [20] where m0 is the free electron mass. In our numerical calculations, we use atomic units in which free electron mass, electronic charge, and the Planck’ s constant have been assumed as unity. The confining potential VD(r) is given by[21]
 |
where V0 is the barrier height and Qc is the conduction band offset parameter which is taken to be 0.6.[1] The band gap difference (Δ Eg) depends on the concentration of Al. In our case Ga1− xAlxAs is the barrier medium in which GaAs dot is embedded. The total energy difference[21] between the dot and barrier media, as a function of x and P, is given by
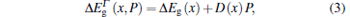 |
where D(x) = [− (1.3 × 10− 3)x]eV/kbar is the pressure co-efficient on the band gap and Δ Eg(x) = 1.155x + 0.037x2 eV. In the present work we choose x = 0.2, then the value of V0 is 147.48 meV for zero pressure. The variation of dot size with pressure is given[19] by
 |
where R0 is the zero pressure dot radius. It is known that da/dP = − 2.6694 × 10− 4a0, where a0 is the lattice constant of GaAs.[22] The hydrostatic pressure dependent conduction band effective masses of the dot layer are obtained from the expression[11]
 |
where P is expressed in GPa (1 kbar = 0.1 GPa).
The pressure used in the numerical work is 0– 4 GPa, which corresponds to 40 kbar. The pressure beyond 4 GPa has not been considered in the present research since the direct to indirect band gap transition of GaAs is at about 4 GPa.[23] The variation of dielectric constant with hydrostatic pressure is given as
 |
The ground state and the excited state eigen-functions in the absence of impurity are given by[24]
 |
 |
where N1, N2, A1, and A2 are normalization constants and α 1, α 2, β 1, and β 2 are given by 

 |
 |
The energy eigenvalues are determined by imposing the Ben Daniel and Duke boundary condition that the normal particle velocity is continuous across the interface

The obtained eigenvalues for the ground state and the excited state are
 |
 |
respectively. Solving these transcendental equations numerically, the confined energies of ground state and excited state are obtained.
When the hydrogenic impurity is placed at the center of the dot, to solve the Schrö dinger equation, we choose a trial wave function as[25]
 |
 |
where λ is the variational parameter. In the presence of impurity, the ground and excited state energies were obtained from the expression

and this can be minimized with respect to variational parameter λ . Here, we obtained the minimum energy Emin(P) by ∂ E(P, λ )/∂ λ = 0. The binding energy of the hydrogen impurity is defined as the difference between the ground state energy of the system in the absence of impurity and the impurity state energy. The ground and excited state donor impurity binding energy are Eb(P) = E0− Emin(P). The expression obtained for Emin is too lengthy; hence, we refrain from giving them here.
The conduction band of GaAs is known to have non-parabolicity and a correction to the effective mass pertinent to the conduction band minimum is given[26] by
 |
where Γ E = 0.0436+ 0.236E2− 0.147E3 in which E is the sub-band energy expressed in meV. Though the present work is interested in ionized impurity scattering, the fact that GaAs is a polar material lacking a center of inversion suggests that it may have additional interactions with various types of phonons, via acoustic, polar optic, and piezoelectric. At any temperature, interactions with all these phonons exist, but their relative dominance may manifest in different temperature regions. Hence, when an experiment on carrier transport is carried out the result is a cumulative effect of all these contributions. Detailed expressions for scattering cross section and relaxation times for each of the above processes are available. An interesting feature is that these effects may be arising due to the polaron mechanisms with an effective Frő hilch coupling constant, such as the polaronic mass which may be obtained from
 |
where

The value of Frő hilch coupling constant for GaAs is taken as 0.26.[27] Here, the binding energy is altered since the effective mass is enhanced by the polaronic effects.
The numerical calculations have been carried out to calculate the donor binding energy of the SQD and the results are presented in Figs. 1– 5.
Figure 1 displays the variation of effective mass with and without non-parabolicity and polaronic mass effect, as a function of the pressure. Due to the applied pressure on the SQD, the effective mass, conduction band non-parabolicity and polaronic mass increase linearly. In addition, the parallel observation was found for the lattice constants, dielectric constant, barrier height, and dot size. Herein, we noticed that the dot radius and barrier height decrease as the effective mass increases.
Figures 2(a)– 2(c) explain the variation of hydrostatic pressure with dot radius, barrier height, and dielectric constant. It is found that the application of pressure linearly decreases the dot radius, barrier height, and dielectric constant, and its effects are impacted in the confined and donor binding energy of the spherical quantum dot.
 | Fig. 2. (a) Variation of dot radius with pressure. (b) Variation of barrier height with pressure. (c) Variation of dielectric constant with pressure. |
The confined energy of the ground and excited states are shown in Fig. 3. From Fig. 3, we can observe that the confined energy decreases as the dot radius increases, which is consistent with the previous reports.[28, 29] The decrease of confined energy is obtained when the effective mass is replaced by the polaronic mass and it further decreases when the hydrostatic pressure is applied. Thus the combined effect of hydrostatic pressure and polaronic mass decreases the total confined energy. For smaller dot sizes less than 30 Å and 65 Å , it is noticed that there is no confinement energy for ground and excited states, since there is no bound state. These results are not applicable to the quantum well because the bound state is present even in the very small sized quantum well.[30]
Figure 4 portrays the variation of ground state donor binding energy for different dot radii with and without pressure and polaronic mass. We observed that the binding energy increases as the dot radius decreases and then diminishes to a limited value corresponding to a particular radius of the dot. When the polaronic effect is induced, the binding energy increases for all dot radii. If the dot radius becomes larger, the effects of donor binding energy on the impurity states become negligible and therefore the energy approaches to the corresponding energy of bulk. This is well matched with the previous report.[25] The donor binding energy reaches zero as the dot size approaches infinity. When the dot radius is extremely large, the confining potential has less influence on the impurity and the wave function approaches the corresponding state of the free space hydrogen atom. It is also seen that the binding energy shows the maximum value at 40 Å , and is a well-known feature in a finite well calculation.[31] When the dots radius approaches to infinity, the binding energy reaches the three-dimensional GaAs, whereas the dot radius is zero, the binding energy in the barrier region. Hence, the confinement becomes negligibly small in the finite barrier model and thus results in giant tunneling. These results are in good agreement with the result of Bella et al.[20]
 | Fig. 4. Binding energy of a hydrogenic donor impurity as a function of dot radius for the ground state. |
The donor binding energy is higher as the hydrostatic pressure becomes stronger as shown in Fig. 4. Thus, the pressure increases the hydrogenic donor binding energy. This is because increasing pressure reduces the dot radius, dielectric constant, and barrier height while the effective mass increases, hence, increases the energy eigenvalue of the system. The temperature effect always decreases the donor binding energy.[25] Hence, we conclude that the pressure and temperature have opposite effects on the donor impurity binding energy. The variation of donor binding energy in the smaller dots also depends on aluminum concentration. For example when x = 0.1 the barrier height is 71.21 meV, x = 0.3 the barrier height is 227.88 meV and x = 0.4 the barrier height is 312.72 meV. As the concentration increases the donor binding energy also increases.[32] In addition, it is very difficult to increase the aluminum concentration x < 0.4, since the indirect band gap nature of Ga 1− xAlxAs. Like other systems when GaAs dots are embedded in a Ga1− xAlxAs matrix, the dielectric mismatch becomes insignificant, especially when x is small. In the absence of pressure, the impurity donor binding energy is about 38.24 meV for R = 50 Å which is in good agreement with Rezaei et al.[33] The maximum contribution to the donor binding energy by the polaronic mass of the ground state is about 19% for the narrow dots.
The binding energies increase to a maximum, and then decrease with the increase of the position of the impurity. Furthermore, we find clearly that the position of the impurity, which is in relation to the maximum value of the binding energy, increases with the increase of orbital quantum number l for fixed n, and for ground states, these maximum values of the binding energy are in relation to the center of the dot. It is because, due to the QD confinement, the electron always tends to localize in the center of the QD; however, because the orbital quantum numbers l = 0, for the excited state, a centrifugal potential will appear, which is equivalent to the case where there is a high barrier for center acting as the repulsive force. The bigger the orbital quantum number l is, the more obvious the effect is.
Figure 5 shows the variation of excited state hydrogenic impurity donor binding energy as a function of dot radius with and without pressure and polaronic mass. The binding energy decreases as the dot radius increases. Since the pressure increases, the electron is pulled towards one side of the quantum dot, resulting in the overall decrease of the binding energies.
 | Fig. 5. Binding energy of a hydrogenic donor impurity as a function of dot radius for the excited state. |
Here, we have seen that the binding energy increases by the application of pressure and polaronic mass. It is found that the smaller quantum dot exhibits the highest donor binding energy due to the geometrical confinement. The binding energy in the excited state reaches a maximum of 27.95 meV at 60 Å in the absence of pressure and polaronic mass. At hydrostatic pressure and polaronic mass, the impurity binding energy reaches a maximum of 31.56 meV at 60 Å . The effect of hydrostatic pressure and polaronic mass has significance only for smaller dot size. The maximum contribution to the donor binding energy of the polaronic mass of the excited state is about 2% for the narrow dots. The different variation of ground state with excited states can be attributed to the nature of electronic density corresponding to ground and excited states and their interactions with the Coulombic potential of impurity.
Figure 6 displays the variation of hydrogenic donor binding energy with different pressures for the ground and excited states. The donor binding energy increases linearly with the pressure. It shows that the donor binding energy of the ground state is lower than the excited state for the dot radii of 150 Å . For smaller dot size, the variation of donor binding energy with and without polaronic effect is larger and its variation is smaller in dot size above 100 Å . For the dot radii of 35 Å , the polaronic effect is enhanced in the ground state. Thus, the donor binding energy is enhanced in an SQD due to the external factors like hydrostatic pressure, conduction band non-parabolicity and polaronic mass. The above enhancement can also be obtained by confined energies, phonon energies, spin– orbit energy, and electron– phonon interaction.[20] We can also tune the band gap of the SQD using concentration of the barrier materials with temperature, electric field, magnetic field, etc. Here, we had tuned the band gap by using hydrostatic pressure, conduction band parabolicity, polaronic mass, and aluminium concentration. Tunability of the band gap of the SQD plays an important role in luminescent and photo voltaic devices.[34]
 | Fig. 6. Variation of binding energy of a hydrogenic donor impurity with pressure for R = 35 Å and R = 150 Å . |
Thus, the confinement in the narrow dot system operating under hydrostatic pressure and polaronic mass may be used to tune the output of the optoelectronic devices without modifying the physical size of the quantum dot. The effect of polaron and donor impurity also plays an important role in the optical communication devices, wave guide splitters, and for integrated optical circulators and isolators.
In this study, we investigated the effects of hydrostatic pressure and polaronic mass on the binding energies of the ground and excited states of an on-center hydrogenic impurity confined in a GaAs/GaAlAs SQD. The numerical calculations were performed to find the donor binding energy. The result showed that the donor binding energies increase to a maximum and then decrease as the dot size increases. The effect of hydrostatic pressure also enhances the donor binding energy. The donor binding energy tends to be zero as the dot radius tends to be infinity for both states. The conduction band non-parabolicity and polaronic effect also reduces the donor binding energy.
The authors would like to thank Prof. K. Navaneethakrishnan, Head and Co-ordinator (Rtd.), School of Physics, Madurai Kamaraj University, Madurai 625021, India for his encouragement and valuable suggestion.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|




