Cite this Article
Geetha P. J., Yashodamma K. O., Sudha . Monogamous nature of symmetric N-qubit states of the W class: Concurrence and negativity tangle* . Chinese Physics B, 24(11): 110302  
Permissions
Monogamous nature of symmetric N-qubit states of the W class: Concurrence and negativity tangle*
Geetha P. J.a), Yashodamma K. O.a), Sudha a),b)
Department of Physics, Kuvempu University, Shankaraghatta, Shimoga- 577 451, India
Inspire Institute Inc., Alexandria, Virginia 22303, USA

†Corresponding author. E-mail: arss@rediffmail.com

*Project supported by Department of Science and Technology, Government of India through the award of INSPIRE fellowship.

Abstract

Using Majorana representation of symmetric N-qubit pure states, we have examined the monogamous nature of the family of states with two-distinct spinors, the W class of states. We have evaluated the N-concurrence tangle and showed that all the states in this family have vanishing concurrence tangle. The negativity tangle for the W class of states is shown to be non-zero, illustrating the fact that the concurrence tangle is always lesser than or equal to the negativity tangle in a pure N-qubit state.

Keyword: 03.65.Ud; 03.67.Bg; monogamy of quantum entanglement; Majorana representation of symmetric pure states; concurrence tangle; negativity tangle
1. Introduction

Monogamy of quantum correlations/entanglement, the quantum mechanical feature indicating the restricted shareability of quantum correlations/entanglement among several parties of a composite system, has evoked great interest in the recent years.[1– 31] The pioneering work of Coffman, Kundu, and Wootters[1] has led to a great deal of activity including issues such as monogamy of quantum versus classical correlations, [5, 21] monogamy using generalized entropies, [14, 17, 18] and monogamy of quantum correlations other than entanglement.[19, 23– 30] Quantifying multi-qubit entanglement is another important issue and measures such as three-tangle (or concurrence-tangle) and negativity tangle, [11] based on monogamy inequality, have been proposed for quantifying residual or three-party entanglement in 3-qubit states. In fact, residual entanglement in a 3-qubit state is defined as the entanglement between the qubits, which is not accounted for by the two-qubit entanglement in the state.[1] The nature of monogamy inequality satisfied by N-qubit states is helpful to quantify the N-qubit residual entanglement, not accounted for by the entanglement in its two-qubit subsystems. In view of the fact[1, 11] that different measures of entanglement give rise to different quantifications of the residual entanglement in 3-qubit pure states, it is natural to expect that similar situation will be realized for N-qubit states also. While it has been shown that generalized (non-symmetric) W states have vanishing concurrence tangle, [1] they are shown to have non-zero negativity tangle.[11] In general, for N-qubit pure states, it was shown that the concurrence tangle is lesser than (or equal to) negativity tangle.[11]

In this work, we examine the nature of monogamy inequality satisfied by N-qubit pure symmetric states belonging to the W class. Here the set of all N-qubit symmetric states (invariant under the interchange of qubits) with only two distinct qubits (spinors) characterizing them is defined as the W class of states, owing to the fact that W states form an integral part of it. We show that the monogamy inequality with squared concurrence[35, 36] as the measure of entanglement holds good with equality for all states of this family (quite similar to the behaviour of W states). With squared negativity of partial transpose[37– 39] as a measure of entanglement, we examine the monogamous nature of the W class of states and show that negativity tangle has non-zero value for all states in this family. We wish to mention here that the Majorana representation of symmetric N-qubit states[32– 34] has enabled us to obtain a simplified form for the states with two distinct spinors, thus helping us to obtain the concurrence tangle and negativity tangle for the whole family of states.

The article is divided into four parts. Section  1 contains introductory remarks. In Section  2, we make use of the Majorana representation of N-qubit pure symmetric states to obtain a simplified form of the states belonging to the W class. We analyze the monogamous nature of the W class of states in Section  3 and evaluate their concurrence tangle and negativity tangle. Section  4 provides a concise summary of the results.

2. Majorana representation of pure symmetric N-qubit states

In order to examine the nature of monogamy inequality satisfied by N-qubit pure symmetric states of the W-class, we make use of the very elegant Majorana representation[32] of pure symmetric states. While several advantages of using the Majorana representation have been reported in Refs.  [33] and [34], we illustrate here its use in identifying the monogamous nature of symmetric states.

In the Majorana representation, [32] a pure symmetric state of N qubits is represented as a symmetrized combination of N constituent spinors | ɛ l〉 as

where

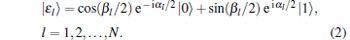Here P̂ corresponds to the set of all N! permutations of the spinors (qubits), and 𝓝 corresponds to an overall normalization factor.

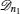
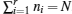
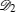
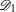
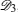
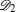
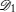
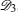
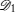
An N qubit pure symmetric state containing r (< N) distinct spinors | ɛ i 〉 (i = 1, 2, … , r), each repeating ni times, belongs to the class , n2, … , nr and each degeneracy configuration {n1, n2, … , nr} (with the numbers ni being arranged in the descending order) corresponds to a distinct SLOCC class.[33, 34] The number of SLOCC inequivalent classes possible for states with r distinct spinors is given by the partition function p (N, r) that gives the distinct possible ways in which the number N can be partitioned into r numbers ni (i = 1, 2, … , r) such that .[33, 34] For instance, a 3-qubit state with only one distinct spinor belongs to the class , where two distinct spinors belong to the class {, 1}and {, 1, 1}is the class of 3-qubit states with three distinct spinors. The classes , , 1 and , 1, 1 are SLOCC inequivalent and a state belonging to one of these classes cannot be converted into the other (different from itself) by any local operations and classical communications.[33, 34] While the class contains only separable states, {, 1} is the W class of states and{, 1, 1} corresponds to the GHZ class of states, thus supporting the fact that three pure qubit states can be entangled in two inequivalent ways.[40]

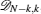
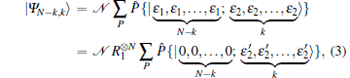A pure symmetric state with 2 distinct spinors belonging to the SLOCC family {, k = 1, 2, … , [N/2] is given by

where ɛ 1 = R1| 0〉 and ɛ 2 = R2| 0〉 , and

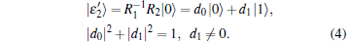Thus, the symmetric state with two distinct spinors | Ψ N− k, k〉 is shown to be equivalent, up to local unitary transformations, to

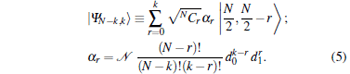It can be seen that α r = δ k, r when d1 = 1, d0 = 0, and the state | Ψ N− k, k〉 reduces to the Dicke state | N/2, N/2 − k 〉 . It is thus not difficult to see that the states in the family DN− 1, 1 (with k = 1) are SLOCC equivalent to the N-qubit W state | N/2, N/2 − 1 〉 .

An arbitrary N-qubit pure symmetric state belonging to the W class is given by

which may be expressed in terms of standard qubit basis as

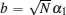
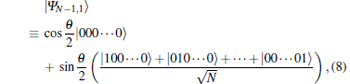where a = α 0, are complex numbers obeying | a| 2 + | b| 2 = 1. On taking a = cos(θ /2), b = sin (θ /2)ei ϕ , (0 < θ < π , 0 < ϕ < 2π ), without any loss of generality and subjecting the N-qubit state  (7) to another local unitary transformation | 0〉 ′ = | 0〉 , | 1〉 ′ = e− i ϕ | 1〉 on all the N qubits, we obtain a further simplified form

with a single parameter θ , 0 < θ ≤ π , describing the state.

3. Monogamous nature of pure symmetric states of the W class: Concurrence and negativity tangle

Having obtained the simplified form of the N-qubit pure symmetric states with two distinct spinors, we will use it to evaluate the concurrence and negativity tangle of this family, and thereby make a statement about their monogamous nature with respect to different entanglement measures. We carry out this task in the following.

3.1. Concurrence tangle

We start by recalling the monogamy inequality in terms of squared concurrence in three-qubit systems introduced by Coffman, Kundu, and Wootters (CKW).[1] They[1] have shown that for any 3-qubit pure state Ψ ABC,

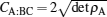
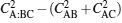
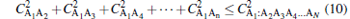where CAB (CAC) is the concurrence between A and B (C), while is the concurrence between system A and BC. The quantity is known as three-tangle or concurrence tangle and is a measure of three-party entanglement.[1] It was also conjectured[1] that a monogamy relation of the form

holds well for all N-qubit pure states. We can term the quantity

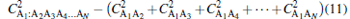as N-concurrence tangle. In fact, it was shown in Ref.  [1] that generalized (non-symmetric) 3-qubit W states given by a| 100〉 + b| 010〉 + c| 001〉 have vanishing concurrence tangle and indicated that their N-qubit counterparts will also exhibit the same feature. We hope to illustrate here that all pure symmetric N-qubit states with two distinct spinors, the W class of states, have vanishing N-concurrence tangle. Towards this end we first evaluate the form of the two-qubit and single-qubit reduced density matrices of the N-qubit state | Ψ N − 1, 1〉 . 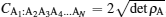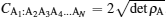Knowing the structure of single qubit density matrices is essential to obtain , the structure of two-qubit (mixed) density matrices is needed for the evaluation of CA1A2. It is worth noting that though the concurrence is defined only for two-qubit systems, the N-qubit state being pure, the (N− 1)-qubits essentially belong to a two-dimensional space and hence one can define the concurrence between a single qubit and the remaining N − 1 qubits.[1] Also, the effective concurrence is the concurrence between two qubits in a pure state leading to . We also need to note here that with | Ψ N− 1, 1〉 being a symmetric state, all its two-qubit and single-qubit subsystems are identical, irrespective of which two qubits or single qubit we choose to consider. That is,

The form of the single-qubit, two-qubit marginals of the state | Ψ N− 1, 1〉 for N = 3, 4, 5, 6 allows us to generalize and obtain these marginals for any N. In Table  1, we have tabulated the structure of reduced density matrices ρ A1A2, ρ A1 of | Ψ N− 1, 1〉 .

Using the form of two-qubit and single-qubit density matrices given in Table  1, we can readily obtain the structure of the two-qubit and single-qubit density matrices of the N-qubit state | Ψ N− 1, 1〉 for any N. We have

Table 1. The single-qubit and two-qubit marginals of | Ψ N− 1, 1〉 for N = 3 to 6.

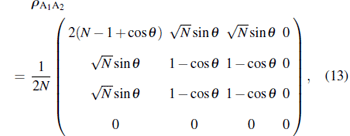and

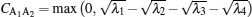
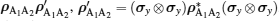
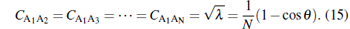The concurrence[35, 36] of the two-qubit state ρ A1A2 is given by , where λ i (i = 1, 2, 3, 4) are the eigenvalues of the matrix . Notice here that the concurrence between any two qubits becomes maximum and is equal to 2/N when θ = π for the W states. In fact this is the maximum bipartite entanglement in an N-qubit state, achievable for W states, as shown in Ref.  [2]. It can be seen that there is only one non-zero eigenvalue λ = (1 − cosθ )2 / N2 for , and we therefore have

Similarly, we obtain det ρ A = (N − 1)(1 − cosθ )2/(4N2) and hence

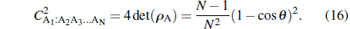As there are N − 1 identical two-qubit subsystem density matrices ρ A1Ai, i = 2, 3, … N, with the first qubit being common to all of them, we have

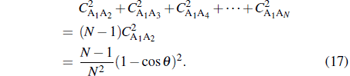Now, we can readily see that (see Eq.  (16))

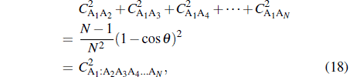thereby establishing the relation

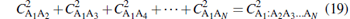for the N-qubit pure states of the W class. Thus, in addition to verifying the monogamy inequality, we have shown that equality holds good for all N-qubit states belonging to the W class. In other words, we have shown that the N-concurrence tangle 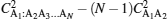vanishes for the family of states | Ψ N− 1, 1〉 .

3.2. Negativity tangle

We begin here by recalling that a monogamy inequality for 3-qubit pure states in terms of negativity-of-partial transpose has been proposed in Ref.  [11]. While the vanishing concurrence tangle for W states indicated only two-way entanglement, the analogous quantity defined by[11]

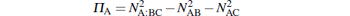
shows a non-zero three-way entanglement in W states. While the concurrence tangle is independent of the focus qubit, the negativity tangle depends on which qubit is considered as the focus qubit. Thus, the negativity tangle for 3-qubit pure states is defined as Π = (Π A + Π B + Π C)/3, with Π A, Π B, and Π C being the negativity tangles with the focus qubits being A, B, and C, respectively.

Quite similar to the case of 3-qubit pure states, the negativity tangle for N-qubit pure states is defined as[11]

where

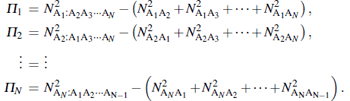
Reference  [1] indicated the vanishing concurrence tangle for N-qubit generalized (non-symmetric) W states, and reference  [11] illustrated that they have a residual N-party entanglement quantified by Π , the negativity tangle. Here, we show that the whole family of pure N-qubit symmetric states belonging to two-distinct spinors (the W class of states) have non-zero negativity tangle. We illustrate this aspect in the following.

Having obtained the two-qubit reduced density matrices of the symmetric state | Ψ N− 1, 1〉 (see Eq.  (13), we can readily evaluate their negativity of partial transpose.[37– 39] The partially transposed density matrix of the two-qubit reduced density matrix ρ A1A2 obtained in Eq.  (13) is evaluated to be

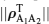
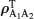
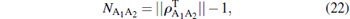The negativity of partial transpose is given by where is the trace norm of the partially transposed density matrix and it is the sum of the square-root of eigenvalues of the positive-definite matrix . As the negativity for a two-qubit system varies from 0 to 0.5, we choose to take NA1A2 to be

so that it varies from 0 to 1, quite similar to the variation of concurrence. In fact, this is the convention adopted for negativity in Ref.  [11], while obtaining the negativity tangle for three-qubit pure states.

As the negativity of a permutation invariant state is identical for any pair of qubits, we denote NA1A2 = NA1Ak, k = 2, 3, … , N. Figure  1 shows the plot of negativity NA1Ak with respect to θ for the W class of states | Ψ N− 1, 1〉 .

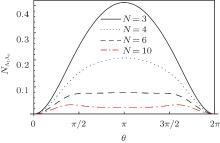Fig.  1. Plot of NA1Ak versus θ in the interval from 0 to 2π for arbitrary N-qubit state belonging to the W class.

It can be seen that with the increase in the number of qubits, the pairwise entanglement quantified by negativity of partial transpose NA1Ak decreases quite considerably.

In Ref.  [11] it was shown that the negativity between the focus qubit and the remaining two qubits of a pure 3-qubit state matches with their concurrence. The authenticity of the relation NA1:A2A3… AN = CA1:A2A3… AN is explicitly verified for N = 3, 4, 5, 6 and thereby generalized to any N, yielding

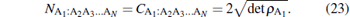The variation of NA1:A2A3… AN with θ , for different values of N, is shown in Fig.  2.

With detρ A1 being (N − 1)(1 − cos θ )2/(4N2), we have the negativity tangle Π 1 as

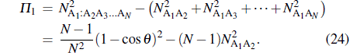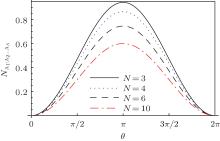Fig.  2. Plot of NA1:A2A3… AN, versus θ in the interval from 0 to 2π for arbitrary N-qubit state belonging to the W class.

However, as we consider symmetric states that are invariant under permutation of qubits, Π 1 = Π 2 = · · · = Π N, and hence,

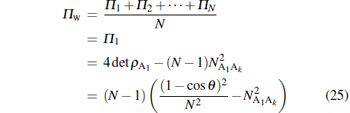is the negativity tangle of the state | Ψ N− 1, 1〉 belonging to the W class. We plot a graph of negativity tangle Π w as a function of θ in Fig.  3.

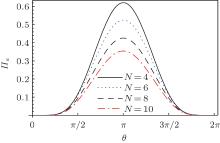Fig.  3. Plot of negativity tangle Π w versus θ for the N-qubit symmetric state belonging to the W class.

In particular, for N-qubit W states, the negativity tangle is given by

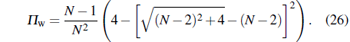Figure  4 shows the variation of negativity tangle with the number of qubits N for N-qubit W states, corresponding to θ = π in | Ψ N− 1, 1〉 .

We have thus accomplished the task of evaluating the negativity tangle for N-qubit pure states belonging to the W class, and illustrated that, not just W states but all the other states in the W class of states have vanishing concurrence tangle. In

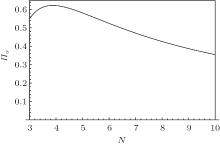Fig.  4. Negativity tangle of N-qubit W states as a function of the number of qubits N. It can be seen that Π w is maximum when N = 4 and decreases with the number of qubits.

addition, we have shown that for all states of the W class, negativity tangle decreases with the increase in N for N ≥ 4. In fact, as can be seen from Figs.  3 and 4, the three-qubit states belonging to the W class have lesser negativity tangle than their four-qubit counterparts. For N ≥ 4, the negativity tangle keeps decreasing monotonically. Moreover, one can observe that though the bipartite entanglement NA1Ak (see Fig.  1) decreases quite drastically with the increase in the number of qubits, the negativity tangle Π w decreases with N more slowly (see Fig.  3). This is due to the slower decrease of the 1 : N − 1 entanglement, quantified through NA1:A2A3… AN, with the increase of qubits (as compared to the fast decrease of NA1Ai with N) (see Figs.  1 and 2).

We would like to mention that the Majorana representation of N-qubit symmetric pure states[32, 34] has enabled us to compute the concurrence tangle and negativity tangle of the whole W class of states. Such a convenient aid available for pure N-qubit symmetric states and not for mixed states is perhaps one of the reasons for the difficulty in verifying monogamy inequality, evaluation of the corresponding tangles in mixed N-qubit states. For N-qubit mixed states, the monogamy inequalities in terms of squared concurrence and squared negativity are, respectively, given by

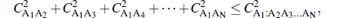
where

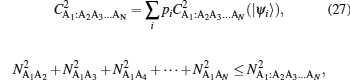where

and ρ = ∑ ipi | ψ i〉 〈 ψ i| is an optimal decomposition of the mixed state ρ that gives minimum value for the RHS in the above relations. The determination of the optimal decomposition of a given mixed state is not trivial. Therefore, the evaluation of concurrence or negativity tangles for mixed states is in general difficult. For 3-qubit states of the form ρ = p | GHZ〉 + (1 − p)| W〉 , the concurrence tangle has been numerically determined to be zero, and an interesting fact that it is an entangled state with zero tangle and zero concurrence has been brought out.[9] A multi-qubit mixed entangled state with no 2− , 3− , … , N – qubit tangles has been reported in Ref.  [13]. An analysis of these kinds of mixed states has recently been given through entanglement indicators obtained through the monogamy relation in squared entanglement of formation.[31] The monogamy inequality in terms of squared negativity has been verified for generalized mixed W states in Ref.  [20]. Despite these results on monogamy relations for mixed states, the difficulty in obtaining optimal decomposition of several mixed states makes the evaluation of their concurrence, negativity tangle, or any such entanglement indicator not very straightforward as in the case of pure states.

4. Conclusion

In this article, we have analyzed the monogamous nature of N-qubit pure states belonging to the W class using squared concurrence and squared negativity as measures of bipartite entanglement. Using the simplified form of the states belonging to the W class, obtained using the Majorana representation of N-qubit symmetric pure states, we have evaluated the N-concurrence tangle and negativity tangle of this family of states. Quite similar to the N-qubit W states, we have shown that all states in the W class of states have vanishing concurrence tangle, but non-zero negativity tangle. It would be of interest to examine the nature of monogamy inequality in N-qubit symmetric states belonging to different SLOCC inequivalent families and compare their concurrence tangle and negativity tangle.

Reference
1 Coffman V, Kundu J and Wootters W K 2000 Phys. Rev. A 61 052306 DOI:10.1103/PhysRevA.61.052306 [Cited within:12]
2 Koashi M Buzek V and Imoto N 2000 Phys. Rev. A 62 050302(R) DOI:10.1103/PhysRevA.62.0503022000 [Cited within:1]
3 Dennison K A and Wootters W K 2001 Phys. Rev. A 65 010301(R) DOI:10.1103/PhysRevA.65.0103012001 [Cited within:1]
4 Terhal B M 2003arXiv: quant-ph/arxiv 0307120 [Cited within:1]
5 Koashi M and Winter A 2004 Phys. Rev. A 69 022309 DOI:10.1103/PhysRevA.69.022309 [Cited within:1]
6 Gour G, Meyer D A and Sand ers B C 2005 Phys. Rev. A 72 042329 DOI:10.1103/PhysRevA.72.042329 [Cited within:1]
7 Osborne T J and Verstraete F 2006 Phys. Rev. Lett. 96 220503 DOI:10.1103/PhysRevLett.96.220503 [Cited within:1]
8 Dong Y 2006 Phys. Lett. A 360 249 DOI:10.1016/j.physleta.2006.08.027 [Cited within:1]
9 Lohmayer R, Osterloh A, Siewert J and Uhlmann A 2006 Phys. Rev. Lett 97 260502 DOI:10.1103/PhysRevLett.97.260502 [Cited within:1]
10 Ou Y C 2007 Phys. Rev. A 75 034305 DOI:10.1103/PhysRevA.75.034305 [Cited within:1]
11 Ou Y C and Fan H 2007 Phys. Rev. A 75 062308 DOI:10.1103/PhysRevA.75.062308 [Cited within:10]
12 Yu C S and Song H S 2008 Phys. Rev. A 77 032329 DOI:10.1103/PhysRevA.77.032329 [Cited within:1]
13 Bai Y K, Ye M Y and Wang Z D 2008 Phys. Rev. A 78 062325 DOI:10.1103/PhysRevA.78.062325 [Cited within:1]
14 Kim J S, Das A and Sand ers B C 2009 Phys. Rev. A 79 012329 DOI:10.1103/PhysRevA.79.012329 [Cited within:1]
15 Lee S and Park J 2009 Phys. Rev. A 79 054309 DOI:10.1103/PhysRevA.79.054309 [Cited within:1]
16 de Oliveira Thiago R 2009 Phys. Rev. A 80 022331 DOI:10.1103/PhysRevA.80.022331 [Cited within:1]
17 Cornelio Marcio F and de Oliveira Marcos C 2010 Phys. Rev. A 81 032332 DOI:10.1103/PhysRevA.81.032332 [Cited within:1]
18 Kim J S and Sand ers B C 2011 J. Phys. A: Math. Theor. 44 295303 DOI:10.1088/1751-8113/44/29/295303 [Cited within:1]
19 Seevinck M P 2010 Quantum Inf. Process 9 273 DOI:10.1007/s11128-009-0161-6 [Cited within:1]
20 Zhao M J, Fei S M and Wang Z X 2010 Int. J. Quant. Inform. 8 905 DOI:10.1142/S0219749910006216 [Cited within:1]
21 Giorgi G L 2011 Phys. Rev. A 84 054301 DOI:10.1103/PhysRevA.84.054301 [Cited within:1]
22 Fanchini F F, de Oliveira M C, Castelano L K and Cornelio M F 2013 Phys. Rev. A 87 032317 DOI:10.1103/PhysRevA.87.032317 [Cited within:1]
23 Prabhu R, Pati A K, Aditi S and Ujwal S 2013 Phys. Rev. A 85 040102(R) DOI:10.1103/PhysRevA.85.0401022012 [Cited within:1]
24 Sudha Usha Devi A R and Rajagopal A K 2012 Phys. Rev. A 85 012103 DOI:10.1103/PhysRevA.85.012103 [Cited within:1]
25 Ren X J and Fan H 2013 Quant. Inf. Comp. 13 0469 [Cited within:1]
26 Liu S Y, Li B, Yang W L and Fan H 2013 Phys. Rev. A 87 062120 DOI:10.1103/PhysRevA.87.062120 [Cited within:1]
27 Streltsov A, Adesso G, Piani M and Bruss D 2012 Phys. Rev. Lett. 109 050503 DOI:10.1103/PhysRevLett.109.050503 [Cited within:1]
28 Bai Y K, Zhang N, Ye M Y and Wang Z D 2013 Phys. Rev. A 88 012123 DOI:10.1103/PhysRevA.88.012123 [Cited within:1]
29 Salini K, Prabhu R, Aditi S and Ujjwal S 2014 Ann. Phys. 348 297 DOI:10.1016/j.aop.2014.06.001 [Cited within:1]
30 Geetha P J and Sudha Usha Devi A R 2014 J. Mod. Phys. 5 1294 DOI:10.4236/jmp.2014.514130 [Cited within:1]
31 Bai Y K, Xu Y F and Wang Z D 2014 Phys. Rev. Lett. 113 100503 DOI:10.1103/PhysRevLett.113.100503 [Cited within:2]
32 Majorana E 1932 Nuovo Cimento 9 43 DOI:10.1007/BF02960953 [Cited within:4]
33 Bastin Tet al. 2009 Phys. Rev. Lett. 103 070503 DOI:10.1103/PhysRevLett.103.070503 [Cited within:4]
34 Usha Devi A R Sudha and Rajagopal A K 2012 Quantum Inf. Process 11 685 DOI:10.1007/s11128-011-0280-82012 [Cited within:6]
35 Hill S and Wootters W K 1997 Phys. Rev. Lett. 78 5022 DOI:10.1103/PhysRevLett.78.5022 [Cited within:2]
36 Wootters W K 1998 Phys. Rev. Lett. 80 2245 DOI:10.1103/PhysRevLett.80.2245 [Cited within:2]
37 Peres A 1996 Phys. Rev. Lett. 77 1413 DOI:10.1103/PhysRevLett.77.1413 [Cited within:2]
38 Horodecki M, Horodecki P and Horodecki R 1996 Phys. Lett. A 223 1 DOI:10.1016/S0375-9601(96)00706-2 [Cited within:1]
39 Vidal G and Werner R F 2002 Phys. Rev. A 65 032314 DOI:10.1103/PhysRevA.65.032314 [Cited within:2]
40 Dür W Vidal G and Cirac J I 2000 Phys. Rev. A 62 062314 DOI:10.1103/PhysRevA.62.0623142000 [Cited within:1]