Many large-scale physical systems consisting of interactive individuals are usually modelled by complex dynamical networks, in which the nodes denote the individuals and the edges denote the interactions among them.^{[1– 10]} Generally, the interactions are denoted by the outer and inner coupling matrices. The outer coupling matrix denotes the topology and the coupling strength of the network, from which one can know whether a pair of nodes affect each other. The inner coupling matrix denotes the interactive manner between a pair of nodes. Take a network coupled with a chaotic Lorenz system as an example, if the first, second, and third components of a pair of nodes affect each other correspondingly, the inner coupling matrix between them is an identity matrix. Due to the complexity of real dynamical networks, the node dynamics and the interactions may be different. Take a dynamical network coupled with chaotic Lorenz and Chen systems as an example, one pair of nodes interact only in the first component, and another pair of nodes interact only in the last component. For better describing this kind of network, namely a colored graph in mathematics, a colored network consisting of colored nodes and colored edges is proposed.^{[9, 10]} Two nodes with different colors have different node dynamics, and two edges with different colors denote the two pairs of nodes have different interactions.

As we know, interactions of a network play a great role in its dynamical behaviour. For example, a dynamical network with different outer and inner coupling matrices can display a totally different synchronization region, ^[11] even discontinuous synchronization regions.^[12] Moreover, the literature has studied the relationship between the network synchronizability and network structural parameters.^{[13, 14]} However, in many real networks, the interactions are not exactly known beforehand. Therefore, how to identify the interactions in a network becomes a hot topic and has been widely studied.^{[15– 24]} Yu et al. suggested a method for estimating the topology of a network for the first time.^[15] Wu et al. identified the topologies of general weighted networks with time-varying coupling delays.^[16] Mei et al. considered the finite-time structure identification of a dynamical network.^[22] In all the above-mentioned literature, the inner coupling matrix is assumed to be known, i.e., only the outer coupling matrix is unknown and to be identified. Naturally, if the outer and inner coupling matrix are both unknown, how to identify them is a challenging and important problem. In particular, the inner matrices of a colored network may be totally different, and how to identify them deserves further studies.

Motivated by the above discussion, this paper considers the identification of interactions in a colored network with the same dimension node dynamics. By introducing proper adaptive laws, an effective network estimator is designed for identifying the unknown interactions. According to the Lyapunov function method and Barbalat’ s lemma, the proof is completed. Section 2 introduces the network model and some preliminaries. Section 3 gives the main result. Section 4 performs a numerical simulation to verify the effectiveness of the derived theoretical result. Finally, Section 5 concludes the paper.

Consider a colored network consisting of N nodes, which can be described by

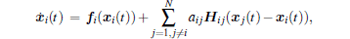where x_i(t) = (x_i1(t), x_i2(t), … , x_in(t))^T ∈ Rⁿ is the state variable of node i, f_i : Rⁿ → Rⁿ is a nonlinear vector-valued function and denotes the local dynamics. Matrix A = (a_ij) ∈ R^{N× N} is the outer coupling matrix and denotes the coupling strength and topology. If there is a connection from node j to node i (i ≠ j), then a_ij ≠ 0; otherwise, a_ij = 0. The diagonal entries of A are zero, i.e., a_ii = 0, i = 1, 2, … , N. Matrix is the inner coupling matrix. If the change rate of the k-th component of node i (i.e., ẋ _ik(t)) is affected by the difference between the l-th components of nodes i and j (i.e., x_jl(t) − x_il(t)), then ; otherwise, .

In this paper, both the outer and inner coupling matrices are assumed to be unknown and need to be identified. Let and , then the problem of identifying a_ij and H_ij becomes the problem of identifying C_ij.

Define . Then, the network (1) can be written as

For identifying the matrices C_ij in network (2), we design the following network estimator:

where i, j = 1, 2, … , N, k, l = 1, 2, … , n, y_i(t) = (y_i1(t), y_i2(t), … , y_in(t))^T ∈ Rⁿ is the state variable of node i in the network estimator, , is the estimation of is the adaptive feedback controller applied on node i, d(t) is the adaptive feedback gain, η and δ are positive constants.

Let e_i(t) = y_i(t) − x_i(t) be the synchronization error, we have the following error system:

Assumption 1 Suppose that there exists a positive L such that (y − x)^T (f_i(y) − f_i(x)) ≤ L(y − x)^T(y − x), i = 1, 2, … , N, holds for any x, y ∈ Rⁿ.

Assumption 2 Suppose that are linearly independent for t > 0.

Barbalat’ s Lemma^[25] If Φ : R → R⁺ is a uniformly positive function for t ≥ 0 and if the limit of the integral exists and is finite, then lim_{t→ ∞} Φ (t) = 0.

Theorem 1 Suppose that Assumptions 1 and 2 hold. Then the unknown matrices of the colored network (2) can be identified by the estimated matrices of the network estimator (3).

Proof Consider the following Lyapunov function candidate:

where d* is an arbitrary positive constant to be determined.

Then the derivative of V(t) with respect to t along the trajectories of Eq. (4) is

where , I_Nn is Nn-dimensional identity matrix, and the matrix C is defined as

Let λ _C be the largest eigenvalue of matrix (C + C^T)/2, then one can choose d* = L + λ _C + 1 such that

Then, one has

and sup_{t≥ 0}V(t) ≤ V(0), i.e., V(t) is bounded. That is to say, e(t) ∈ L₂ and e(t) are bounded, i.e., E(t) ∈ L_∞ . From error system (4), Ė (t) exists and is bounded for t ∈ [0, + ∞ ). According to Barbalat’ s lemma, we obtain lim_{t→ ∞} e(t) = 0, followed by lim_{t→ ∞} ė (t) = 0. Then, as t → ∞ , converges to the following largest invariant set:

which is equivalent to

From Assumption 2, we have . That is, the coupling matrices of network (1) are identified when the synchronization between networks (2) and (3) is achieved. Thus, the proof is completed.

Remark 1 In colored network (1), the inner coupling matrices H_ij need not be diagonal. If the inner coupling matrices H_ij are diagonal, i.e., for k ≠ l, then the adaptive laws about in (3) can be replaced by for k ≠ l and , k = 1, 2, … , n, i, j = 1, 2, … , N.

In this section, a simple colored network consisting of 3 colored nodes and 3 colored edges is considered in a numerical example to verify the effectiveness of the obtained result, which is shown in Fig. 1. The first, second, and third node dynamics are chosen as the Lorenz system^[26]

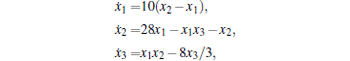
Chen system^[27]

and Lü system^[28]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. A simple colored network consisting of 3 colored nodes and 3 colored edges. The red, green, and blue nodes are chosen as the Lorenz, Chen, and Lü systems, respectively.

The outer and inner coupling matrices in Fig. 1 are chosen as follows:

In numerical simulations, choose η = 5, δ = 5, the initial values , and d(0) = 10. Moreover, choose the initial values of x_i(t) and y_i(t) randomly. From Fig. 2, one can find , and converge to 0.2, and others converge to 0 as t → ∞ , which yields a₁₂ = 0.2, . That is, the interactions between nodes 1 and 2 are identified. Similarly, from Figs. 3 and 4, we have a₁₃ = 0.1, a₂₃ = 0.1, , and . That is, all the interactions in the colored network are identified.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The orbits of , k, l = 1, 2, 3. Clearly, , and converge to 0.2 and others converge to 0 as t → ∞ , which yields a12 = 0.2 and . That is, the interactions between nodes 1 and 2 are identified.

Remark 2 In the above numerical example, for simplicity, a colored network consisting of 3 colored nodes and 3 colored edges is considered. From the network model (1) and the proof of Theorem 1, a colored network considered in this paper consists of N nodes. That is, the proposed method in this paper can handle the networks with more than 3 nodes.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The orbits of , k, l = 1, 2, 3. Clearly, , , converge to 0.1 and others converge to 0 as t → ∞ , which yields a13 = 0.1, . That is, the interactions between nodes 1 and 3 are identified.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The orbits of , k, l = 1, 2, 3. Clearly, , , and converge to 0.3 and others converge to 0 as t → ∞ , which gives a23 = 0.1, . That is, the interactions between nodes 2 and 3 are identified.

In this paper, the identification problem of a colored dynamical network is considered. Compared with the existing results about the identification problem of dynamical networks, not only the outer coupling matrix but also the inner coupling matrices are unknown and need to be identified. The inner coupling matrices can be totally different. For identifying the unknown interactions (outer and inner coupling matrices), an effective network estimator with proper adaptive laws is designed. According to the Lyapunov function method and Barbalat’ s lemma, the result is rigorously proved. Finally, a numerical example is provided to illustrate the effectiveness of the obtained result.

Though the node dynamics of the colored network considered in this paper can be different, they have the same dimension. In real networks, the node dynamics may have different dimensions. How to design an effective network estimator for identifying the interactions of a colored network with different-dimensional node dynamics is a challenging problem and deserves further studies. On the other hand, if the node dynamics of a colored network are also unknown, how to extend the topology identification methods from observed dynamical time series, such as Granger causality^[20] and compressive sensing^{[8, 24]} method, to identify the unknown interactions of a colored network will be considered in our future work.