†Corresponding author. E-mail: songmapnet@163.com
*Project supported by the Technology and Development Research Project of China Railway Corporation (Grant No. 2012X007-D) and the Key Program of Technology and Development Research Foundation of China Railway Corporation (Grant No. 2012X003-A).
Routing and path selection are crucial for many communication and logistic applications. We study the interaction between nodes and packets and establish a simple model for describing the attraction of the node to the packet in transmission process by using the gravitational field theory, considering the real and potential congestion of the nodes. On the basis of this model, we propose a gravitational field routing strategy that considers the attractions of all of the nodes on the travel path to the packet. In order to illustrate the efficiency of proposed routing algorithm, we introduce the order parameter to measure the throughput of the network by the critical value of phase transition from a free flow phase to a congested phase, and study the distribution of betweenness centrality and traffic jam. Simulations show that, compared with the shortest path routing strategy, the gravitational field routing strategy considerably enhances the throughput of the network and balances the traffic load, and nearly all of the nodes are used efficiently.
Since the small-world effect[1] and the scale-free property[2] of complex networks have been found, scholars have studied the statistical characteristics of many real systems and acquired a lot of achievements. The complex network theory has been widely applied to computer, transportation, physical, biological and other fields.[3– 10] Scholars have tried to find the inner relations between the structure and the function of the system, so as to provide corresponding strategies for solving practical problems, such as cascading failure, chaos, traffic congestion, etc.[11] With the continuous growth of packets, how to improve the network capacity and optimize the traffic congestion has become a key problem of network research.[11, 12] Congestion is a dynamics phenomenon that exists in many real complex systems, and is assumed to be a phase transition from free-flow to congestion. From this perspective, one of the fundamental problems we face nowadays is to find an optimal strategy for packet delivery between a given sending node and its destination node.[11]
Research about routing strategy has mainly focused on three aspects. The first aspect is the global routing strategies, as represented by the shortest path algorithm, which chooses a minimum cost as the best route for packet delivery. This kind of routing strategy is prone to traffic congestion, and some nodes with large degree or betweenness bear severe congestion.[13, 14] From the perspective of global routing control, Yan et al. suggested an effective path algorithm that takes the degree of node as a parameter reduces the probability of occurring of congestion of large degree nodes.[15] Bogdan et al. pointed out that the capacity of the network is limited by the amount of traffic each link can support, and suggested that the transport capacity of the network is maximized by using a set of routes that minimize the maximum betweenness of the nodes.[16] Shen et al. proposed a self-organizing shortest path finding strategy based on thermal flux diffusion on complex networks, the shortest paths between the source and the other nodes are found to be self-organized by comparing node temperatures.[17] The second aspect is the local routing strategies, which mainly consider the local information or adjacent information; specific strategies include random walk, first-order neighborhood search, second-order neighbor search, etc.[18, 19] The third aspect is the mixed routing strategies, which take into account the local information of the current node, the shortest path from the current node to other nodes and the cache, and other factors. In recent years, scholars have made a lot of researches about the mixed routing strategies.[20– 22] Echenique proposed a random routing strategy that a packet could be sent to a neighbor of the current node at a certain probability.[20] Zhao et al. proposed a neighborhood load routing metric for wireless mesh networks, and constructed a method of measuring the average value of path neighborhood load, which can be integrated into existing routing strategies to further improve the routing efficiency.[21] Considering the effect of the information feedback on traffic system, Dong et al. studied the dynamics of traffic flow with real-time information and presented advanced prediction feedback strategies with cellular automaton (CA) model in two- and multi-route traffic systems, which can guide road users to make a choice.[23– 25] On the basis of this, Chen et al. proposed the vacancy length feedback strategy and the exponential function feedback strategy, which are both proven to be effective.[26, 27]
The aim of studying routing strategies is to improve the network throughput. Previous research has indicated that the throughput of a network is inversely proportional to the maximum betweenness centrality of its nodes on a fixed network scale.[28] Therefore, reducing the maximum betweenness centrality can enhance network capacity. Inspired by this argument, some scholars optimized routing strategies by minimizing the maximum betweenness centrality of nodes.[29– 31] Generally, the nodes with large betweenness centrality can attract most packets and also the congestion is easy to emerge. To some extent, these nodes are of greater attraction to packets than small degree nodes. Therefore, some scholars have studied the traffic flow, network congestion, and routing process by using the gravitational field theory.[32– 38] Qian and Han[32] proposed a spatial network based on the optimal expected traffic calculated by the gravity model and simulated the Chinese city airline network, according to which they[33] further presented a weighted spatial network by establishing the improved gravity equation, and found that a linear and a nonlinear strength-degree correlation can emerge when considering and neglecting the “ transport effect respectively. Jung et al.[34] investigated the traffic flows of the Korean highway system and found that the traffic flow between cities forms a gravity model. Maniadakis and Varoutas[35] studied network congestion by using gravity model and found that the network topologies created based on the gravity model suffer less congestion than the random, the scale-free or the Jackson-Rogers ones. For network transport, Liu and Li[36] defined a gravitational field equation considering the real traffic congestion of nodes, and the routing protocol mainly considers the shortest paths between the neighbors and destinations.
Overall, current studies mainly focused on the distribution of real traffic flow by using the gravity model; although reference [36] presented a routing strategy based on gravitational field theory, the strategy only considered the shortest paths between the neighbors and destinations. In the present paper, we will further study the interaction between the node and the packet and consider the real traffic congestion and potential traffic congestion of nodes. Each node can attract packet to pass through it and the delivery of each packet is always influenced by the gravitational field of all nodes. Thus, this paper will borrow from the gravitational field theory and study the network transport process.
The remainder of this paper is organized as follows. In Section 2, we introduce the traffic flow model and define the gravitational field model of a node to the packet, which is used to describe the attraction between the node and the packet, and then propose a routing strategy by borrowing the idea from the gravitational field theory. In Section 3, we introduce some metrics for evaluating the transmission performance of routing strategies and discuss the experiments and results. In Section 4 some conclusions are drawn from the present study.
We use the Barabá si– Albert (BA) scale-free model for simulation. The traffic model is described as follows: all nodes are endowed with the functions of sending and receiving; at each time step, R, packets are generated in the network with randomly chosen sources and destinations, and can deliver at most ci packets towards their destinations; the cache queue length of each node is assumed to be unlimited and the first-in-first-out (FIFO) discipline is applied at each queue. If one of the neighbors is the packet destination, then the packet is delivered directly to its target. Otherwise, the packet is delivered to a neighbor under the routing protocol. Moreover, once a packet arrives at its destination, it will be removed from the network.
Generally, network congestion emerges first at the node with large degree or large betweenness, and then spreads to the other nodes, which is obtained by adopting the shortest path algorithm. Actually, it is necessary to avoid some large degree (or betweenness) nodes intentionally so as to reduce the probability of occurring of congestion of these nodes and reduce the waiting time of packets within the cache queues, and improve the network capacity. But, if all of the packets are destined to avoid these nodes with large degree or betweenness, which will make these nodes become leisure and aggravate the load of other nodes, this will trigger the drift of network congestion. From the viewpoint of the network game, we need to consider two problems: (i) how to measure the traffic congestion or unblocked reliability of a node in a dynamical transport environment, and (ii) how to avoid the congested nodes and choose other nodes to deliver packets.
Evaluating the congestion degree of nodes is very important to explore high efficient routing protocols. To some extent, the congestion degree of a node reflects the centrality of the node in the process of network transport. A very different concept of centrality is betweenness centrality, which measures the extent to which a node lies on paths between other nodes. For the shortest path routing strategy, the betweenness centrality is unevenly distributed: the traffic congestion first begins to emerge at the large betweenness nodes. Theoretically, the ratio of the node capacity to the number of packets in its queue reflects the unblocked reliability of the node. The betweenness centrality can be used to describe the potential congestion of the node under a routing strategy and, correspondingly, the inverse of betweenness centrality reflects the potential unblocked reliability of the node. With this in mind, we consider both the real traffic congestion and the possible potential congestion of the node and define a model for measuring the unblocked reliability of the node as follows:

where Ji is the unblocked reliability of node i; ci is the transmission capacity of node i in unit time step; qi is the number of packets waiting for transmission in the cache queue of i; Bi is the betweenness centrality of node i under the shortest path algorithm; and, μ is a parameter which is used to adjust the influence of the betweenness on the overall unblocked reliability of the node, μ > 0.
To a certain extent, the betweenness centrality reflects the ability to connect the nodes. From the viewpoint of gravitation theory, we can regard betweenness centrality as the attraction of the node to the packet, and the larger the betweenness centrality of the node, the greater the attraction of the node to the packets within the network is. Considering Eq. (1), we can consider that the greater the unblocked reliability of the node, the greater the attraction of the node to the packet is. Therefore, we can see that the attraction affecting the packet during network transport is similar to the gravity affecting the object in the gravitational field. Borrowing the idea of the gravitational field theory, packet delivery over a network can be described in accordance with gravitational field theory as follows. At each time step, the packet is always attracted by all the nodes and the node always attracts the packets within the queues of other nodes. The attraction between a node and a packet relates to the unblocked reliabilities of both nodes, the distance between the node and the packet, but not to the packet itself. Suppose that a packet is at node j. The attraction of some node i to the packet can be defined as
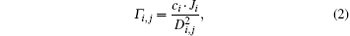
where Γ i, j is the attraction of node i to the packet at node j; Ji can be considered as the unblocked reliability of node i; ci is the transport capacity of node i; and, Di, j is the shortest path length between node i and node j. In light of the gravitational field equation, the gravity of the node for packets is proportional to the product of the transmission capacity and the unblocked reliability of the node, but inversely proportional to the square of the shortest path length between the node and the packet. Therefore, we can see that equation (2) shows a similar meaning to that in the classical gravitational field theory. We need to note that equation (2) is different from the gravitational field model in Ref. [36], because reference [36] only considers the real traffic congestion of the node. However, our model considers both the real traffic congestion and the potential traffic congestion of the node, and so it may be more effective to reduce the congestion to a large degree or betweenness nodes.
Considering the attraction of the node to the packet, we can control the delivery process of packets by improving the transmission efficiency of greater attraction nodes. However, if the routing strategy only considers the attractions to local adjacent nodes, it hardly ensures that the packets can reach their destinations as quickly as possible. The efficiency of a routing strategy depends on whether it can send every packet to its destination in the shortest travel time. Equation (1) indicates that the smaller the attraction between a node and packet, the more severe the node congestion is. Therefore, we can see that if the routing strategy can optimize the travel paths of packets by adjusting the node attraction, it will effectively control the traffic congestion of the network. Theoretically, to change the travel path of packet considering the traffic states of the neighbors can update the node gravity. However, it cannot improve the travel path of packets because the travel distance may be too long. We should consider the traffic state or attraction of more nodes. Therefore, in this paper, the path gravity is introduced to evaluate the attraction of the travel path to the packet. Suppose that the packet is at node v and its destination is node t. Let U(v) be the set of the neighbors of v, Uk(i, t) be the set of all the nodes on the k-th path from i (i ∈ U(v)) to t, and pi, t be the number of paths from i to t, then we will consider all the possible paths (not only the shortest path). Therefore the model is defined as follows:
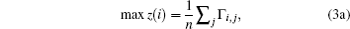
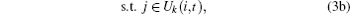
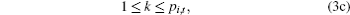

where (1/n)Σ jΓ i, j can be regarded as the attraction of the shortest path between node i and t to the packet along the kth path from i to t, n is the number of nodes within the set Uk(i, t). On the basis of above model, in this paper we propose a gravitational field routing strategy, and the transmission principle is detailed as follows: obtain the neighbor set U(v) of node v; for each neighbor i (i ∈ U(v)), if the packet path does not contain i, obtain all the paths from i to t, and extract Uk (i, t) for each path, and then calculate the gravities of all the nodes for the packet; and, choose the neighbor a with maximal path gravity as the next routing node of the packet.
For our routing strategy, the packets are always delivered along the path with maximum gravity, which indicates that the routing strategy always chooses the more unblocked paths to deliver the packets. Importantly, it needs to note that the suggested routing strategy is different from the method in Ref. [36] in that our method considers more possible paths besides the shortest paths.
3.1.1. Order parameter
To improve routing protocols we need to enhance the transport capacity of the network. We focus on the throughput of the network that can be measured by the critical point of phase transition from free state to congestion. In order to describe the critical point of the network capacity accurately, we use the order parameter introduced in Ref. [39]:
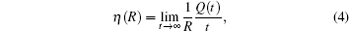
where Q(t) is the number of packets within the network at time t. For R < Rc, η (R) = 0, indicating that the system is in free state with no traffic congestion. Otherwise, for R > Rc, η (R) → r where r is a constant larger than zero, the system will collapse ultimately. Therefore, the capacity of the entire system can be measured by the critical generating rate Rc at which a continuous phase transition will occur from a free flow phase to a congestion phase.
3.1.2. Betweenness centrality
To evaluate the transmission performance of our routing strategy, betweenness centrality is introduced to measure the utilization of nodes. In this paper, we introduce the betweenness centrality defined by Liu et al.[36– 38]
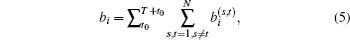
where bi is the total number of packets passing through node i over time window [t0, T + t0]; 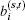
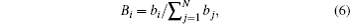
where Bi is the betweenness centrality of node., the greater the value of Bi, the more the nodes passing through the node i are, so Bi reflects the aggregation of connection capacity of i.
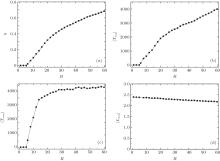
To illustrate that the gravitational field routing strategy is superior to the shortest path routing strategy in enhancing network capacity and diminishing traffic congestion, we use the BA scale-free network with the network size N = 100, m0 = m = 4 and node capacity c = 1 for simulations, and introduce the order parameter η , average travel time 〈 Tavg〉 , maximum travel time 〈 Tmax〉 and average travel distance 〈 Lavg〉 to measure the transmission performance of routing strategies. Figure 1 shows the variations of the order parameter η , maximum travel time 〈 Tmax〉 , average travel time 〈 Tavg〉 , and average path distance 〈 Lavg〉 with R, obtained under the shortest path routing strategy. The results indicate that η , 〈 Tmax〉 and 〈 Tavg〉 all increase abruptly when R > 5, which means that a phase transition from a free state phase to a congested phase occurs at R = 5. Thus, the transport capacity of the network is Rc = 5 for the shortest path routing strategy.
The curves of the order parameter η , average travel time 〈 Tavg〉 , maximal travel time 〈 Tmax〉 and average travel distance 〈 Lavg〉 versus the generation rate R for the gravitational field routing strategy are illustrated in Fig. 2. The results indicate that for R ≤ 20, η , 〈 Tmax〉 and 〈 Tavg〉 are all small and stable; however, for R > 20, η , 〈 Tmax〉 and 〈 Tavg〉 all increase abruptly, which indicates that the critical generation rate is Rc = 20. The average travel distance 〈 Lavg〉 presents a trend of “ first increase and then decrease” , and when R = 20, 〈 Lavg〉 reaches a maximum. The reason for this is that when the generation rate R is very small, the traffic flow is in a free state, the packets are delivered along the shortest path, so the average travel distance 〈 Lavg〉 is very small; with the increase of R, some nodes begin to collect packets, but because of the guidance of the gravitational field routing strategy, the network does not sink into congestion. The travel paths of the packets avoid most of the large degree and betweenness nodes and do not deliver along the shortest path; therefore, the average travel path 〈 Lavg〉 increases gradually. With increasing R, and when R > Rc, the network sinks into congestion abruptly, more and more nodes collect lots of packets, and then many packets will hardly reach their destinations, which will reduce the efficiency of the gravitational field routing strategy.
Therefore, we can conclude that our routing strategy better considers the traffic congestion of all the nodes and greatly enhances the throughput of the network.
To further illustrate that our approach is highly efficient, the experiments compared with the routing strategy in Ref. [36] are carried out in Fig. 3. The results indicate that, compared with the method presented in Ref. [36], our routing strategy improves the throughput of the network by 25 percent, and when the traffic flow is in a congested phase and R keeps unchanged, the congestion decreases to some extent. Moreover, figure 3(b) shows that when R is very small (R ≤ 13), the average travel distance 〈 Lavg〉 is approximately the same for both routing strategies, because the traffic is in a free-flow phase, the transmission process of our approach is similar to that in Ref. [36]; for 13 < R < 30, 〈 Lavg〉 increases to some extent compared with that in Ref. [36], because when R is some great, the packets within the network increase, our approach may choose all of the possible paths to deliver packets (not only the shortest path between the neighbors and destinations presented in Ref. [36]); therefore, the travel paths will be longer. Consequently, we can conclude that compared with the routing strategy of Ref. [36], the proposed routing strategy considers the gravities of more paths and further improves the transport capacity of the network.
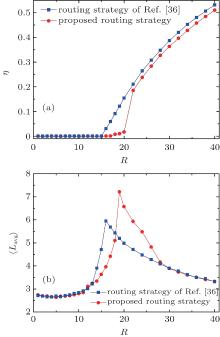 | Fig. 3. Simulation results of the routing strategy presented in Ref. [36] and our approach, showing (a) order parameter η values versus R; (b) average path distance 〈 Lavg〉 values versus R. Other parameters are network size N = 100, m0 = m = 4, and c = 1. |
In Eq. (1), parameter μ is used to adjust the influence of the betweenness centrality on the overall unblocked reliability of the node. Then, we need to analyze the dynamical characteristics of μ in transport process. The simulation results of the critical capacities for different μ values are illustrated in Fig. 4. We can see that the network transport is sensitive to μ ; the throughput of the network is lower for too great or too small μ ; and, when μ = 0.5, the throughput reaches the maximum Rc = 20. The reason for this is that when μ is too small, the traffic congestion of large betweenness nodes cannot be controlled effectively, so the throughput is lower; and, when μ is too great, our routing strategy cannot enough use the nodes with large betweenness in the shortest path algorithm to deliver packets, the gravities of these nodes are too small and will be useless to a great extent. Therefore, we can conclude that the routing strategy should properly control the attractions of the nodes with large betweenness centrality.
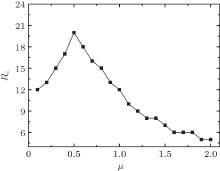 | Fig. 4. Curve of Rc versus μ for the gravitational field routing strategy. The results show the maximal Rc = 20 at μ = 0.5. The other parameters are network size N = 100, m0 = m = 4, and c = 1. |
To further study the transmission performance of the proposed routing strategy, we investigate the distributions of betweenness centrality under different values of generation rate R as shown in Fig. 5 for the shortest path routing strategy, and figure 6 shows the results for the gravitational field routing strategy. The simulations indicate that for the shortest path routing strategy, the betweenness centrality is most inhomogeneously distributed. Although the inhomogeneous degree of distribution is reduced with increasing R, the betweenness centrality is still unevenly distributed obviously. Compared with the shortest path routing strategy, the gravitational field routing strategy has a betweenness centrality distribution that is totally homogeneous. The distribution presents a trend of “ inhomogeneous– homogeneous– inhomogeneous” . When the generation rate R is very small, such as R = 1, the distribution of betweenness centrality is inhomogeneous. Because the traffic state is in a free flow phase, the packets are most delivered along the shortest path, the transmission process is similar to that of the shortest path routing strategy. With the increase of R, the transport performance of the gravitational field routing strategy is gradually inspired, and most of nodes are used efficiently. So, the distribution of betweenness centrality is gradually and increasingly homogeneous, and the betweenness of each node is approximately equal to 0.01 when R ≈ 20. However, with the continuous increase of R, the traffic congestion begins to emerge within the network, some nodes will become increasingly congested, the betweenness centrality will become inhomogeneously distributed to a certain extent. But overall, the congestion of the nodes with a large degree is distinctly alleviated compared with that for the shortest path routing strategy, and the distribution of the betweenness centrality is most homogeneous.
 | Fig. 5. Distributions of betweenness centrality for the shortest path routing strategy under different values of R. The other parameters are network size N = 100, m0 = m = 4, and c = 1. |
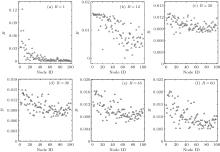 | Fig. 6. Distributions of betweenness centrality for the gravitational field routing strategy under different values of R. The other parameters are network size N = 100, m0 = m = 4, and c = 1. |
The free state refers to the balanced state between created and removed packets at each time step, and when the number of packets more than Rc, the system will ultimately enter into the jammed state, which will result in the continuously accumulating of packets in the network and only a few packets can reach their destinations. Therefore, we also study the congestions of the network nodes through counting up the number N(p) of the packages in the cache queue of node, as shown in Fig. 7 for the traffic congestions of the shortest path routing method, the gravitational field routing strategy presented in Ref. [36], and the proposed gravitational field routing strategy. The results indicate that our routing algorithm and the algorithm of Ref. [36] can both relieve the congestion degree of the whole network to a great extent and balance the distribution of the traffic flow. Compared with the shortest algorithm, the proposed routing strategy reduces the maximal congestion degree by about 17 times. Compared with the method of Ref. [36], our approach further reduces the maximal congestion degree to a great extent. Moreover, we can see that for the three routing strategies, the distributions of node congestions are the same for different values of generation rate R, which means that when the network is in a congested phase, the utilization rate of each node is not changed for different values of R.
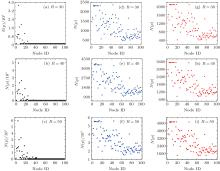 | Fig. 7. Distributions of node congestions under different values of R, showing the results of (a)– (c) shortest path routing strategy, (d)– (f) the routing strategy of Ref. [36], (g)– (i) the proposed gravitational field routing strategy. |
For the sake of alleviating the traffic congestion and improving the network capacity, we present a routing strategy borrowing the idea from the gravitational field theory. A gravitational field equation is defined to describe the attraction of the node to the packet, which better considers the travel distance and the unblocked reliability of the node. On the basis of this equation, we define a model for measuring the gravity of the travel path for the packet and then propose a simple routing strategy. To test the transmission performance of the gravitational field routing strategy, a BA scale-free network is used as a case study. Simulation results show that, when compared with the shortest path algorithm, our method improves the network throughput several times, greatly balances the traffic load, and reduces the network congestion, especially the nodes with large degree or betweenness centrality. Compared with the gravitational field routing protocol of Ref. [36], the proposed approach is more efficient with greater throughput and smaller congestion Therefore, we can conclude that our study further reveals the mechanism of the gravitational force of nodes during network transport, presents a stable and highly efficient routing protocol, and explores the traffic congestion and routing strategy.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|