In rare earth transition metal intermetallics, the nature of the interaction between the 3d magnetism of the transition metal and the localized 4f magnetism of the rare earth ions is of primary interest. Among them, doped CeFe₂ compounds exhibit intriguing magnetization jumps across the antiferromagnetic (AFM) to ferromagnetic (FM) transition, which shows characteristics resembling those in the martensitic scenario.^{[1, 2]} A similar jump behavior has been reported in many kinds of materials, such as intermetallic germanide Gd₅Ge₄, ^{[3, 4]} mixed-valent manganite Pr_0.6Ca_0.4MnO₃, ^{[3, 5, 6]} multiferroic Y₂CoMnO₆, ^[7] cubic NaZn₁₃-type polycrystalline Pr_0.2La_0.8Fe_11.4Al_1.6, ^[8] mixed-spin oxide FeTiO₃-Fe₂O₃, ^{[9, 10]} and some other materials.^{[11, 12]} Among the family of the cubic C15 MgCu₂-type Laves phase compounds RFe₂ (R = rare earth), Ouyang et al. studied the mixing effects of light and heavy rare earths in Nd_{1 − x}Tb_xCo₂.^[13] Besides, the magnetic and magnetostrictive properties of Pr_xNd_{1 − x}Fe_1.9 alloy^[14] and some bulk MgCu₂-type rare-earth iron compounds^[15] were studied. Previously, scientists have studied the structural, magnetic, and magnetostrictive properties of the quasi-quaternary intermetallic compounds (Tb_0.2Pr_0.8)(Fe_0.4Co_0.6)_{1.93 − x}B_x, ^[16] (Tb_0.2Pr_0.8)(Fe_0.4Co_0.6)_{1.93 − x}C_x, ^[17] and Tb_{1 − x}Pr_x(Fe_0.4Co_0.55 B_0.05)_1.93, ^[18] in which a small amount of doped C/B which occupies preferentially the interstitial sites can effectively inhibit the formation of the 1:3 PuNi₃-type phase.

In the present work, we mainly investigate the low-temperature magnetic properties of intermetallic compounds Tb_{1 − x}Pr_x(Fe_0.4Co_0.6)_1.88C_0.05 (x = 0, 0.8, and 1) by detailed susceptibility measurements, in order to figure out the influence of the spin structure in R-site on the meta-magnetic transition and the observed magnetization jump behavior similar to that of doped CeFe₂ compound^[12] in our Pr-containing samples. Furthermore, the time relaxation, field sweep rate, and cooling field dependence of sharp jumps of Pr(Fe_0.4Co_0.6)_1.88C_0.05 compound are investigated by specified measurement protocols, which shows the characteristics of the martensitic scenario.

Polycrystalline samples of Tb_{1 − x}Pr_x(Fe_0.4Co_0.6)_1.88C_0.05 (x = 0, 0.8, and 1) were synthesized by conventional arc melting in high-purity argon (10^{− 3} Pa). The purity of the constituents was 99.9% for Tb and C, 99.99% for Fe and 99.8% for Co, respectively. The ingots were homogenized at 700 ° C (for the sample of x = 0.8) and 900 ° C (for the samples of x = 0 and 1) for seven days in high-purity argon atmosphere, which were then quenched in ice water. X-ray diffraction (XRD, Philips X’ pert pro) data were measured at room temperature with Cu Kα radiation (1.54 Å ). Magnetization (M) data were acquired using a vibrating sample magnetometer on a commercial superconducting quantum interference device (SQUID-VSM Quantum Design, Inc.). Temperature (T) dependences of the zero-field cooled (ZFC) and field cooled (FC) magnetization, M(T), were measured between 1.8 K and 380 K at selected magnetic fields (H). The ZFC isothermal magnetization was measured after cooling the sample from 380 K to selected temperatures.

The x-ray diffraction patterns of powdered Tb_{1 − x}Pr_x (Fe_0.4Co_0.6)_1.88C_0.05 (x = 0, 0.8, and 1) samples at room temperature are shown in Fig. 1. From the results it can be seen clearly that Tb_0.2Pr_0.8(Fe_0.4Co_0.6)_1.88C_0.05 consists of single MgCu₂-type Laves phase (space group ), due to the fact that low C-content can effectively inhibit the formation of the impurity phase, which is consistent with the result reported previously.^[17] However, a small amount of the PuNi₃-type impurity can be still observed in Tb(Fe_0.4Co_0.6)_1.88C_0.05, the deviation expected may be attributed to improper C-concentration and sintered temperature.^[18] For Pr(Fe_0.4Co_0.6)_1.88C_0.05, the main phase is the MgCu₂-type Laves phase, and the secondary phase is the PuNi₃-type phase, coexisting with a small number of rare earth phases. The phase of this compound is sensitive to the annealing process and much attention has been paid to the effects of annealing protocols on similar materials in recent years.^{[19– 21]}

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The XRD patterns of powdered Tb1 − xPrx(Fe0.4Co0.6)1.88C0.05 (x = 0, 0.8, and 1) compounds at room temperature.

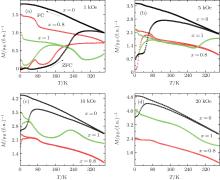
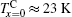
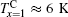
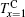
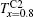
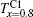
Temperature dependences of magnetization of Tb_{1 − x}Pr_x (Fe_0.4Co_0.6)_1.88C_0.05 (x = 0, 0.8, and 1) compounds measured in ZFC and FC modes under various magnetic fields are shown in Fig. 2. For the sample with x = 0 as shown in Fig. 2(a), an obvious anomaly emerges at the ZFC branch when , indicating the appearance of an AFM– FM magnetic transition. The magnetization is observed to increase with increasing temperature, indicating that the magnetic moments are gradually rearranged into parallel alignments, resulting in the development of FM phase in the AFM matrix. As the temperature increases further, the magnetization starts to decrease, revealing that the ordered FM moments become partially disordered. For the FC M(T) curve, the ordered FM content increases progressively with reducing temperature, and a frozen behavior is observed around , which is indicative of the balance between the AFM and FM phases in the low temperature regime. For the sample with x = 1 as shown in Fig. 2(a), the AFM– FM magnetic transition of the ZFC M(T) curve is observed at . With increasing temperature, the FM content increases until the temperature reaches ∼ 160 K. Further, higher temperature causes the magnetization to reincrease, which may be caused by the impurities in the sample, and this phenomenon is consistent with the aforementioned XRD result. And the FC M(T) curve is almost identical with the ZFC curve in the temperature region higher than 160 K, and multiple magnetic states are frozen around . For the sample with x = 0.8 as shown in Fig. 2(a), the ZFC M(T) curve displays two anomalies, respectively, at and , suggesting the coexistence of two AFM phases in this sample. The magnetization at the FC branch is frozen successively around and with reducing temperature. For each of the samples (x = 0 and 1) containing single rare earth, only one anomaly at the ZFC M(T) curve is observed in the lower temperature region. In comparison, two anomalies occur for the mixed rare-earth sample (x = 0.8), which is related to the mixing effect of light and heavy rare earths. For each of the samples, a large irreversibility between the ZFC and FC M(T) curves is observed in a wide temperature region, which is gradually suppressed by increasing the external magnetic field. The distinction becomes almost invisible for the samples with x = 0.8 and 1 when H = 20 kOe (1 Oe= 79.5775 A· m^{– 1}.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. M(T) plots of Tb1 − xPrx(Fe0.4Co0.6)1.88C0.05 (x = 0, 0.8, and 1) compounds in ZFC and FC modes under an external magnetic field of (a) 1 kOe, (b) 5 kOe, (c) 10 kOe, and (d) 20 kOe, respectively. The unit 1 Oe = 79.5775 A· m– 1.

In order to further investigate the effects of the Tb ions and/or the Pr ions on the magnetic properties of Tb_{1 − x}Pr_x(Fe_0.4Co_0.6)_1.88C_0.05 compounds, the five-quadrant M(H) isotherms at 1.8 K are shown in Figs. 3(a)– 3(c). To take into consideration the effects of external variables, all of the measurements are carried out based on the specified protocol; that is, the samples are demagnetized at 380 K and then zero-field cooled down to 1.8 K with dT/dt = 10 K/min, and the measurements are performed at a magnetic field sweep rate of 50 Oe/s. The number and located branches of magnetization jumps observed across the AFM– FM transitions for the samples with x = 0.8 [Fig. 3(a)] and x = 1 [Fig. 3(b)] are exactly the same. However, the former has a higher critical magnetic field of each jump, and the curves between adjacent jumps are inclined with respect to the H-axis, which is different from the H-axis-parallel plateaus of the latter. In clear contrast, the M(H) isotherm of the sample with x = 0 [Fig. 1(a)] shows a smooth magnetic transition behavior with no abrupt change in magnetization. The data presented in Figs. 3(a)– 3(c) indicate that the occurrence of magnetization jump is strongly related to the light lanthanide Pr ions rather than the heavy Tb ions.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. M(H) isotherms of Tb1 − xPrx(Fe0.4Co0.6)1.88C0.05 compounds with (a) x = 0.8, (b) x = 1, and (c) x = 1 at 1.8 K. (d) M(H) isotherms of all the compounds under the external magnetic field expanded to ± 70 kOe.

In order to analyze the saturated (M_S) and remanent (M_r) magnetization of Tb_{1 − x}Pr_x(Fe_0.4Co_0.6)_1.88C_0.05 compounds, we expand the external magnetic field to ± 70 kOe in the M(H) measurement as shown in Fig. 3(d). Unlike the zero remanent magnetization in doped CeFe₂ compounds, ^{[1, 2]} the value of M_r is high in our samples, which can be used to classify the materials into type-1 and type-2 materials, as proposed in Ref. [7]. The values of M_S and M_r are listed in Table 1, from which it can be obtained that the mixed rare-earth Tb_0.2Pr_0.8(Fe_0.4Co_0.6)_1.88C_0.05 compound has the largest M_S in all of the three samples. This phenomenon can be interpreted as follows. i) For Tb(Fe_0.4Co_0.6)_1.88C_0.05, the 4f electrons of the heavy lanthanide Tb ions couple antiferromagnetically with the 3d electrons of the transition metal Fe(Co) ions, ^{[22– 25]} and the Tb– Tb magnetic moments couple ferromagnetically.^[26] ii) For Pr(Fe_0.4Co_0.6)_1.88C_0.05, parallel alignments are formed between the light Pr 4f electrons and Fe(Co) 3d electrons, as well as the magnetic couplings between spins of Pr ions.^[26] iii) For mixed rare-earth compound Tb_0.2Pr_0.8(Fe_0.4Co_0.6)_1.88C_0.05, besides the AFM/FM couplings between Tb/Pr 4f electrons and Fe(Co) 3d electrons, there exist anti-parallel alignments between spins of Tb ions and those of Pr ions. This also explains that the samples (x = 0 and 1) containing single rare earth element correspond to single magnetic transition, relative to double transitions in the mixed rare earths sample (x = 0.8), as observed in Fig. 2. In addition, the ratio of M_S/M_r (= 39.9%) for the sample with x = 1 is minimum while that for the sample with x = 0.8 (M_S/M_r = 88.3%) is maximum.

Table 1.

Table 1.

Table 1. Values of MS and Mr of Tb1 − xPrx(Fe0.4Co0.6)1.88C0.05 compounds (x = 0, 0.8 and 1). Content x MS/μ B · (f.u.)− 1 Mr/μ B · (f.u.)− 1 MS/Mr x = 0 5.11 2.63 51.5% x = 0.8 2.64 2.33 88.3% x = 1 4.44 1.77 39.9%

Table 1. Values of MS and Mr of Tb1 − xPrx(Fe0.4Co0.6)1.88C0.05 compounds (x = 0, 0.8 and 1).

The abrupt changes in magnetization can be ascribed to the avalanche-like growth of FM clusters in the vicinity of the critical magnetic field as observed in doped CeFe₂ compounds which show martensitic scenario.^{[1, 2]} In this regard, detailed magnetization measurements are performed in Pr(Fe_0.4Co_0.6)_1.88C_0.05 sample, including the temperature, relaxation time, field sweep rate and cooling field dependence of magnetization jumps, in order to examine the intrinsic characteristics of martensitic transition in this sample.

Figure 4 shows the influence of temperature on the jumps observed in the M(H) isotherm. As shown in Fig. 4(a), at stage 1 (0 → 20 kOe), when T = 1.8 K and H < 5 kOe, the slope of the data is apparently greater than that observed in the sample with x = 0.8 [Fig. 3(a)], suggesting that the AFM ground state of Pr(Fe_0.4Co_0.6)_1.88C_0.05 is less stable than that of the sample with x = 0.8. With increasing magnetic field, the slope becomes bigger and an abrupt jump in magnetization is observed at H = 13 kOe. At stage 2 (20 kOe → 0 kOe), a smooth FM– AFM transition is observed, in clear contrast to the almost constant FM content of the sample with x = 0.8 at the same M(H) branch. And three magnetization jumps are observed during the reorientation of the FM moments at stage 3 (0 → − 20 kOe). Stage 4/5 is the reverse process of stage 2/3. By comparison with the case of Tb_0.2Pr_0.8(Fe_0.4Co_0.6)_1.88C_0.05, the number of jumps decreases more rapidly with the increase of temperature, indicating that the intermediate magnetic states in Pr(Fe_0.4Co_0.6)_1.88C_0.05 are more sensitive to thermal fluctuation.

Fig. 4.

	Figure Option ViewDownloadNew Window
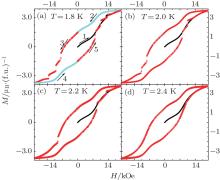	Fig. 4. M(H) isotherms of Pr(Fe0.4Co0.6)1.88C0.05 at (a) T = 1.8 K, (b) 2.0 K, (c) 2.2 K, and (d) 2.4 K.

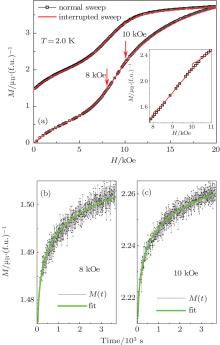
It can be demonstrated from Fig. 5(a) that the measurement protocol can also induce the appearance of abrupt magnetization jumps. At T = 2 K, the acquired data show no jump behavior in the normal sweep. Meanwhile, in the interrupted sweep, magnetic fields of 8 kOe and 10 kOe are maintained for 3000 s, giving rise to additional magnetization jumps. In the maintaining time, magnetization data are recorded as a function of time, as shown in Figs. 5(b) and 5(c). Both of the M(T) curves can be well fitted by the stretched exponential function M(t) = M₀ exp[– (t/τ )^β ], ^{[7, 27– 30]} where τ is the relaxation time of the magnetic spin, and β is the stretching exponent (0 < β < 1). The magnetic relaxation behavior observed from the M(t) curves indicates that the magnetic state at a low temperature resembles a glassy state, ^{[3, 6, 27]} and also suggests that the magnetization jumps are dependent on the dynamics of the martensitic strain distribution.^[2]

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. (a) ZFC M(H) isotherms of Pr(Fe0.4Co0.6)1.88C0.05 at T = 2.0 K in a normal sweep and in an interrupted sweep. Two magnetic fields of 8 kOe and 10 kOe are maintained for 50 min in interrupted sweep. The inset shows the magnified jumps. (b) and (c) The corresponding time revolution of isothermal magnetization during the waiting time in interrupted sweep. The green thick lines represent the stretched exponential fittings.

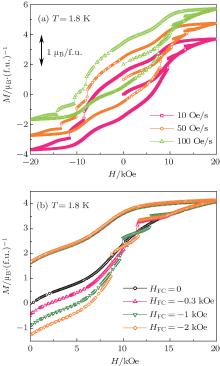
From Fig. 6(a) it is clearly seen that the magnetic field sweep rate significantly affects the number and critical field of magnetization jump, which is reminiscent of the martensitic scenario in this compound.^{[2– 4, 6, 7]} In a metamagnetic system, the critical field of magnetization jump is generally related to the field cooling process. Figure 6(b) shows the initial and second branches of the M(H) isotherms of Pr(Fe_0.4Co_0.6)_1.88C_0.05 at T = 1.8 K under negative cooling fields (– H_FC); however, no jump behavior is observed under + H_FC (data are not shown). This phenomenon can be well explained by using the AFM– FM interface model proposed in Ref. [7] when discussing the effect of cooling fields on the jump behavior in multiferroic Y₂CoMnO₆. When the cooling field is negative, the induced FM content aligns oppositely to the external magnetic field, while the spins on the AFM side due to the interface coupling align along the external magnetic field, promoting the magnetic jump, ^{[4, 7]} making the elastic energy decrease. With the increasing strength of | H_FC| , the number of magnetization jumps increase, meanwhile the corresponding critical fields shift to a lower field region. The time relaxation, field sweep rate, and cooling field dependence of magnetization jumps in Pr(Fe_0.4Co_0.6)_1.88C_0.05 compound show the behaviors similar to those observed in doped CeFe₂^{[1, 2]} and multiferroic Y₂CoMnO₆, ^[7] suggesting the existence of the martensitic scenario in these materials.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (a) M(H) isotherms of Pr(Fe0.4Co0.6)1.88C0.05 at T = 1.8 K, measured with field sweep rates of 10 Oe/s, 50 Oe/s, and 100 Oe/s. The curves are vertically shifted for clarity. (b) Initial and second branches of the M(H) curves of Pr(Fe0.4Co0.6)1.88C0.05 at T = 1.8 K after cooling down with negative magnetic fields of – 0.3 kOe, – 1 kOe, and – 2 kOe, compared with the ZFC M(H) one.

In this work, we investigated the magnetic properties of intermetallic Tb_{1 − x}Pr_x(Fe_0.4Co_0.6)_1.88C_0.05 compounds (x = 0, 0.8 and 1). Only in the Pr-containing samples (x = 0.8 and 1) were sharp magnetization jumps observed across the AFM– FM transition associated with the avalanche-like growth of FM clusters. The experimental results suggest that the jumps accompanied by the intermediate metastable states are determined by the light lanthanide Pr ions. Meanwhile, the step-like behavior can also be observed in the interrupted sweep condition or under the negative cooling field. In addition, the time, field sweep rate, and cooling field dependence of jump behavior confirm the martensitic scenario in the Pr(Fe_0.4Co_0.6)_1.88C_0.05 compound.