Thin films are widely recognized in the realms of experimental and applied science, the manufacture of electronics, optics, packaging, ^{[1– 4]} and the structural and magnetic properties of multilayers.^{[5– 13]} The bilayer Ising model is an appropriate model to investigate the magnetic properties of thin films. Moreover, the bilayer honeycomb lattice (BHL) has attracted enormous interest in both experimental and theoretical research. It has a similar structure consisting of two layers, such as AA and AB  stacking  geometries of graphene. Recently, the magnetic properties of different graphene structures have been studied by the various theoretical methods within the Ising model.^{[14– 19]} We should also mention that in the BHL a number of novel phenomena have been found, such as the quantum Hall effect, quantum spin Hall effect, chiral superconductivity, and coulomb interaction.^{[20– 31]} Furthermore, a layer anti-ferromagnetic and paramagnetic insulator phase has been observed in the BHL. Although previous work has mainly focused on the electronic properties of BHL, ^{[32– 35]} a phase diagram for the magnetic phase transition induced by the interaction and dimers is still lacking.

The Ising model is a well-known pioneering theoretical model that is widely used in magnetic systems and which plays an important role in understanding in-depth the phase transitions and critical phenomena. Recently, thin films have been widely studied by means of Monte Carlo (MC) simulations, ^{[36– 41]} mean-field approach (MFA), ^{[42– 44]} and the effective-field theory (EFT)^{[45– 51]} along with well-known theoretical methods in equilibrium statistical physics in the literature of Ising systems.

Despite these studies, as far as we know, the hysteresis and compensation behaviors of BHL Ising system have not been investigated. In this paper, we study the magnetic behaviors of BHL with AB stacking geometry, in which the study of the gap gives interesting results in different stacking geometries. In this way, the effects of interaction parameters on the hysteresis shape, the compensation type and phase diagrams of BHL are discussed within the framework of the EFT with correlations, in which the EFT considers partially spin-spin correlations without introducing mathematical complexity by using the Van der Waerden identities and provides results that are quite superior to those obtained by using the MFA. On the other hand, the EFT method takes into consideration the fluctuation of the effective field and correctly accounts for the correlations at the same site, so it can well reflect the physical essence of the system.^{[52– 54]} Therefore, when applied to a BHL system, the EFT method can yield results that will be expected to be comparable to those of the MC simulation method. Thus, in spite of its limitations, the EFT is an adequate starting point for studying this kind of spin system. It should be noted that although the results of the MC method are rather reliable, it is always constrained by the speed of the computer.

The rest of the present paper is arranged as follows. In Section  2, we give the model and its formalism in the EFT with correlation. The detailed numerical results and discussions are presented in Section  3. Finally, Section  4 is devoted to a summary and some conclusions.

We investigate the magnetic properties of spin-1/2 Ising BHL system shown in Fig.  1 within the effective field theory. We use EFT with correlations to obtain the EFT equations for the system. This method was first introduced by Honmura and Kaneyoshi, ^[55] and Kaneyoshi et al., ^[56] and is a more advanced method that deals with Ising systems than the mean-field theory (MFT) because it considers the correlations. Each site in Fig.  1 is occupied by the spin-1/2 Ising particle. The Ising Hamiltonian of the BHL system can be written as

where and correspond to the spin of each layer and take values ± 1/2 at each site; 〈 ij〉 and 〈 mn〉 indicate a summation over all pairs of nearest-neighboring sites of each layer; J_A and J_B are the exchange constants for the first and second layer, respectively, which are also called intralayer coupling constants; and, J_Int is the interlayer coupling constant over all of the adjacent neighboring sites of layers.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic representation of BHL system. The blue and red spheres, and green and yellow spheres indicate magnetic atoms at the A and B sublattices, respectively.

Now, within the framework of EFT with correlations, one can easily find the magnetizations for the BHL as follows:

where and are the magnetizations on A upper layer, respectively, and similarly and represent the magnetizations on B lower layer, respectively. ∇ = ∂ /∂ x is a differential operator and the functions f(x + h) are defined by

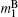
where β = 1/k_BT_A, with T_A being the absolute temperature, and k_B the Boltzman factor. By using the definitions of the order parameters in Eqs.  (2a)– (2d), the total magnetizations of per site (M_T) can be defined as

By solving these equations, we can obtain the magnetic properties of spin-1/2 BHL. We will perform the calculations in the next section.

In this section, we investigate the hysteresis and compensation behaviors, and phase diagrams of a spin-1/2 BHL system by using the formulation given in Section  2. Particularly, we study the effects of the Hamiltonian on hysteresis loops and compensation types of the system.

3.1. Compensation behaviors

We investigate the behavior of total magnetization (M_T) as a function of temperature and obtain compensation types of a spin-1/2 BHL system. Figure  2 shows the temperature dependences of M_T for several values of J_A, J_B, and J_Int. As seen from Fig.  2, the system exhibits four types of compensation behaviors, namely L-, Q-, P- and S-type compensation behaviors. The Q- and P- types of compensation behaviors classified in the Né el theory, ^[57] and L-, and S- types were obtained by Strecka.^[58] The Q-type behavior shows a monotonic decrease of the M_T with increasing temperature, and it then illustrates a steep decrease of the total magnetization just in the vicinity of the critical temperature. The P-type behavior displays the temperature-induced maximum with increasing temperature. The behavior of L-type curve is very similar to the P-type behavior, which has a temperature-induced maximum, except that the M_T starts from zero. The S-shaped behavior initially exhibits a steep decrease of the M_T, and then it again shows a second steep decrease in the vicinity of critical temperature. In Fig.  2(a), the curves are marked for fixed values of J_A = − 0.5 and J_Int = 1.0, and selected values of J_B from − 1 to − 0.1. This figure shows the S-type and Q-type compensation behaviors. With increasing J_B, the S-type compensation behavior turns into the Q-type compensation behavior, and then again turns into the S-type. Moreover, in Fig.  2(b), the curves are marked for a fixed value of J_B = − 1.0 and J_Int = 0.1, and selected values of J_A from − 1 to − 0.1. This figure shows the Q-type and S-type compensation behaviors. With increasing J_A, the S-type compensation behavior turns into the Q-type compensation behavior. As seen from Fig.  2(c), all of the curves display L-type compensation behaviors. In Fig.  2(d), all of the curves display P-type compensation behaviors. Moreover, one should notice that the compensation behaviors have been experimentally obtained in Ref.  [59], and have been theoretically predicted in different Ising systems.^{[60– 65]} It is also worth mentioning that recently the compensation behaviors have been theoretically obtained in kinetic Ising systems.^{[66– 68]}

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. Total magnetization dependences on temperature for different values of interaction parameters. The system exhibits the L-, Q-, P-, and S-types of compensation behaviors. (a)  For the fixed values of JA = − 0.5 and JInt = 1.0, and selected values of JB from − 1 to − 0.1. (b)  For the fixed values of JB = − 1.0 and JInt = 0.1, and selected values of JA from − 1 to − 0.1. (c)  For the fixed values of JA = 0.1 and JB = 0.5, and selected values of JInt from − 1 to − 0.1. (d)  For the fixed values of JA = 0.1 and JB = − 0.5, and selected values of JInt from 1 to 0.1.

3.2. Hysteresis behaviors of a bilayer honeycomb lattice

In this subsection, we examine the effects of the temperature and interaction parameters on the hysteresis behaviors of a BHL system.

3.2.1. Temperature effects

In Fig.  3, we illustrate the dependences of hysteresis loop of BHL system on the temperature (T_emp = 0.1, 0.2, 0.3, 0.4, and 0.5) at J_A = 0.5, J_B = 0.5 and J_Int = 0.5. We can see that the magnetization curves are symmetric for both positive and negative values of the external magnetic field. We can also see that the hysteresis loops decrease with increasing temperature and they then disappear for a temperature above the critical temperature T_C = 0.35. The physical means of this fact is that while at low temperatures the system becomes a hard magnet, with the increase of the temperature the hard magnet turns into a soft magnet. Similar results are observed in some experimental^{[69– 74]} and theoretical studies.^{[75– 77]} On the other hand, we plot the hysteresis loops for fixed values of J_A = 0.5, J_B = 1.0 and J_Int = − 0.5, and selected values of T_emp = 0.02, 0.15, 0.25, 0.4, and 0.65. In Figs.  4(a)– 4(c), the hysteresis loop is a double loop. With the increase of temperature, the double hysteresis loop turns into a single hysteresis loop, as seen in Fig.  4(d), and if the temperature is higher, then the single hysteresis loop disappears in the case of T_emp > T_C (T_C = 0.57), as seen in Fig.  4(e). The reason for this fact is that all of the magnetic moments fluctuate with a relaxation time shorter than the measuring time at high temperature values. Thus, magnetizations become very small and consequently the external magnetic field needed to reverse magnetic moments will be less.^{[78, 79]}

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Effects of the temperature on hysteresis behavior for Temp = 0.1, 0.2, 0.3, 0.4, and 0.5, and fixed values of JA = 0.5, JB = 0.5, and JInt = 0.5.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Effects of the temperature on the hysteresis behavior  for fixed values of JA = 0.5, JB = 1.0, and JInt = − 0.5, and selected values of Temp = 0.02, 0.15, 0.25, 0.4, and 0.65.

3.2.2. Effect of interaction parameters

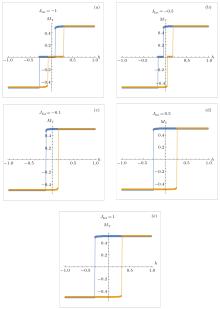
To better understand the effects of interlayer (J_Int) and intralayer (J_A or J_B) couplings on the hysteresis loop, we plot the M_T curves versus the applied field h in Figs.  5 and 6. In the case of J_A = 0.5, J_B = 0.5, and T_emp = 0.1 fixed values, figure  5 is obtained for selected five typical J_Int values, namely J_Int = − 1.0, 0.5, 0.1, 0.5, and 1.0, to present the interlayer coupling dependences of the hysteresis behaviors. When the interaction between A and B layers has a low value, the system displays double hysteresis loop behavior. In other cases, the system shows a single hysteresis loop behavior correspondingly, and with an increase in the value of J_Int, the single hysteresis loop becomes grater, as seen in Figs.  5(c)– 5(e). Moreover, figure  6 shows the dependences of hysteresis loops of a BHL system on an intralayer coupling for fixed values of J_Int = 0.5, J_B = 0.5, and T_emp = 0.1. In the figure we can see that with increasing ferromagnetic coupling, the single central hysteresis loop becomes larger.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Interlayer coupling dependences of the hysteresis behaviors for JA = 0.5, JB = 0.5, and Temp = 0.1, fixed values, and selected five typical JInt values, namely JInt = − 1.0, 0.5, 0.1, 0.5, and 1.0

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Intralayer coupling dependences of the hysteresis behaviors for JA = 0.5, 2.0, and 3.0 and fixed values of JInt = 0.5, JB = 0.5, and Temp = 0.1.

3.3. Phase diagrams of bilayer honeycomb lattice in (T_emp, J_B, J_Int) and (T_emp, J_A, J_B) planes

Figures 7 and 8 show the influence of the interaction parameters on the phase diagram of a BHL system. In these figures, the system only displays the second-order phase transition lines; hence, the system does not show the tricritical point (TCP). The phase diagrams are divided into two phase regions, namely: paramagnetic (p) phase and ferromagnetic (f) phase regions. In Fig.  7, we see that by increasing and reducing the J_B value, the phase transition temperature increases. From this figure, we also observe that the phase transition temperature changes less with an increasing or reducing J_Int value.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Phase diagram of BHL system in the (Temp, JB, JInt) plane for JA = 1.0.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. Phase diagram of BHL system in the (Temp, JA, JB) plane for JInt = 0.5.

We should also mention that the transition temperature found by solving the coupled Eq.  (2) for the AB stacking geometry of the present BHL system, increases with an increase in the correlation in the system with AA stacking geometry.

We study, within the concept of EFT with correlation, the hysteresis and compensation behaviors as well as phase diagrams of the Ising system with a bilayer honeycomb lattice (BHL) structure, and we also examine the effects of the interaction parameters on the magnetic properties of the system. We observe that, besides a single hysteresis loop, double hysteresis loops could possibly occur in the system. Furthermore, we also obtain the four compensation types, namely L-, Q-, P-, and S-types, from the thermal variations of the total magnetization under certain conditions of the interaction parameters.

We hope that our detailed theoretical investigation may stimulate further research of the magnetic properties of bilayer systems, and will also motivate experimentalists to investigate the compensation and hysteresis behaviors.