Cite this Article
Li Hui-Ran, Cheng Xin-Lu†, Zhang Hong, Zhao Feng. Influences of neutral oxygen vacancies and centers on α-quartz . Chinese Physics B, 24(10): 106105  
Permissions
Influences of neutral oxygen vacancies and centers on α-quartz
Li Hui-Rana), Cheng Xin-Lu†a),b), Zhang Honga),c), Zhao Fengd)
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
Key Laboratory of High Energy Density Physics and Technology of Ministry of Education, Sichuan University, Chengdu 610065, China
College of Physical Science and Technology, Sichuan University, Chengdu 610065, China
Laboratory for Shock Wave and Detonation Physics Research, Institute of Fluid Physics, China Academy of Engineering Physics, Mianyang 621900, China

†Corresponding author. E-mail: chengxl@scu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11176020 and 11374217) and the Doctoral Program of Higher Education of China (Grant No. 20100181110080).

Abstract

Our calculations demonstrate that the concentration of neutral oxygen vacancies can affect the geometrical structrue, electronic structure, and optical properties of α-quartz. Moreover, the distribution of the neutral oxygen divacancy can also exert some influence on the properties of α-quartz. The dissimilarity and similarities are presented in the corresponding density of state (DOS) and absorption spectrum. In addition, when a higher defect concentration is involved in α-quartz, the influence of center on the geometry of α-quartz becomes more significant. However, the introduction of an center barely results in any improvement compared with the influence produced by the corresponding neutral defect.

PACS: 61.72.–y; 42.70.Ce; 71.90.+q
Keyword: α-quartz; neutral oxygen vacancy; center; concentration and distribution of defects
1.Introduction

The intrinsic point defects can markedly affect material properties.[1– 5] For instance, point defects can cause the transmittance band position of multiphase zirconia film to shift[6] and enlarge the friction of carbon nanotube.[7] And the oxygen vacancies have a significant effect on the phonon mode of hexagonal HoMnO3 thin film.[8] While among the point defects generated in silica (SiO2) material, [9– 12] the oxygen vacancy (VO) is one of the most point harmful defects. It has been found that the VO is a dominant element in the percolation of SiO2 and is responsible for the breakdown in electric-field strength.[13– 15] The VO vacancy can increase the hole tunneling current passing through α -quartz.[16] In addition, when the number of VO vacancies increases, the leakage current can almost exponentially rise.[17] Therefore, VO has been extensively investigated from silica clusters[18] to solid materials.[19] In particular, a considerable amount of work has been carried out to investigate the α -quartz with deficient centers, [20, 21] including the theoreticalal study by using the density functional theory (DFT).[22, 23] According to the generalized gradient approximation (GGA) calculations, Kang et al.[24] indicated that a network of oxygen vacancies can drastically increase the gate leakage current. Furthermore, it has been found that the formation of the VO chain is energetically feasible once the isolated VO vacancies are created.[24] And Nadimi et al.[17] also reported a similar phenomenon that there is an attractive interaction between two neutral vacancies.

When the oxygen vacancy in α -quartz is exposed to radiation, the center, which appears as the center in amorphous SiO2, is a general generated center. Marshall et al.[25] observed that oxygen deficient centers can be converted into E′ centers after gamma irradiation. And the center has been studied experimentally and theoretically.[12, 26, 27] However, there is also a controversy over the structure of the center. For example, there are several configurations provided for the center, such as O3 ≡ Si· + Si ≡ O3[18, 28– 30] and O2 = Si · – O– + Si = O2.[13, 31] But the universally accepted point is that the positively charged oxygen vacancy is considered to be the model of center. For example, Lenahan and Dressendorfer[32] pointed out that the positive charge can be fixed at the neutral VO, allowing the formation of the center. In the case of the stability of the center, Chadi[33] considered that the positively charged oxygen vacancy is unstable in α -quartz, but the thermodynamic stability was provided by Carbonaro et al.[34]

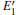
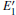
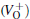
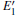
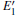
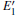
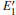
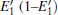
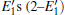
Because the above-mentioned defects have a major influence on the SiO2 materials, a complete understanding of them can help to improve the quality. It is necessary to make a further study of the neutral VO and center. In the present work, we focus on studying the two interior defects located within the bulk of α -quartz and not on the surface. Especially, we attempt to discuss the effects of the concentration and distribution of the two types. Although the concentration and distribution of VO vacancies have been considered in previous works, [17, 24] while the used SiO2 layers are sandwiched between the Si structures. In this case, the effect of the concentration and distribution of VO vacancies on the SiO2 material has not been reported. Hence, both neutral VO and centers are introduced into the α -quartz with a maximum number of 2 to produce an expected concentration. So two types of neutral VO models can be distinguished as follows: a single VO (1– VO) and two VOs (2– VO). In the same way, the center also has two types as follows: a single and two . On the basis of the successful applications of the first-principles DFT, [35] which has been used to investigate the VO[36] and neutralize supercells with charged defects, [37, 38] the DFT is also applied in the calculations.

2.Calculation method

The periodic supercell applied in our investigation contains 72 atoms, which are obtained by 2a × 2b × 2c superlattice. The lattice parameters[39] of the used primitive cell are a = b = 4.913  Å , c = 5.4052  Å , α = β = 90° , and γ = 120° . The space group of the primitive cell is P3121, and there are three formula units per cell, that is to say, there are three Si atoms and six O atoms. The primitive cell in the supercell is shown by a dotted line in Fig.  1(a). According to Ref.  [19], the neutral VO is created by removing the O atom from its  lattice  site in the intact crystal. With the purpose of producing a concentration of defects, one and two oxygen atoms are removed to establish 1– VO and 2– VO defects, respectively. So we have the vacancy concentration of 1.4% and 2.8%, respectively. To investigate the distribution of defects, a larger 8- membered (i.e. 8 Si– O– Si bonds) ring is chosen to vary the position of the VO. Therefore, the two oxygen vacancies are separated by different numbers of Si– O– Si bonds (0, 1, 2, or 3 Si– O– Si bonds). For convenience, the model of two adjacent VOs (separated by 0 Si– O– Si bond) is denoted as 2a– VO, and the oxygen divacancy separated by 1, 2, or 3 Si– O– Si bonds are represented by 2b1– VO, 2b2– VO, and 2b3– VO, respectively.

To build the model with the center, a net positive charge is appended to one of the two Si atoms neighboring the neutral vacancy. Like the neutral oxygen divacancy, the two centers can also be separated by 0, 1, 2, or 3 Si– O– Si bonds, and the types are identified as and respectively. The positive charge can be arbitrarily assigned to one of the two neighboring Si atoms; thus, two models for each center can be constructed. Consequently, we investigate the effects caused by changing the location of the positive charge.

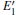
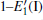
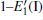
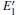
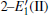
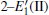
With the formation of the oxygen divacancy, two pairs of adjoining Si atoms (marked as Si1, Si2, Si3, and Si4) remain with the two VOs. In addition, Si2 and Si3 are adjacent to each other, and Si1 and Si4 are at the ends. The introduction of a positive charge into the system with the 2– VO center results in the model with one VO and one . If the positive charge is fixed on the Si2 or Si3 atom, the type of defect is denoted as , and when the positive charge lies on the Si1 or Si4 atom, the defect is marked as . As for the model with two , two positive charges are applied to the two VOs. The defect is defined as two positive charges lying on Si2 and Si3. The defect is defined as two positive charges locateed at Si1 and Si3, or Si2 and Si4. When the charges are located at Si1 and Si4, the defect is denoted as .

The relaxation of the related structures is performed at zero pressure by using the GGA– PBE and ultrasoft pseudopotentials.[40] All of the calculations are carried out by using the CASTEP software.[41] In the relaxation process, the total energy convergence accuracy is set to be 2.0× 10− 5  eV/atom and the maximum force acting on atom is 0.05  eV/Å . Additionally, the volume and cell shape are also relaxed, except for the atomic positions. The 4 × 4 × 4 Monkhorst– Pack k-point grid is used for the Brillouin zone integration. The maximum energy cutoff value for plane wave expansion is 340.0  eV. The optimized configurations of α -quartz with neutral VOs can be distinguished in Fig.  1.

Fig.  1. Configurations of α -quartz with different types of neutral VO: (a) without defect, (b) 1– VO, (c) 2a– VO, (d) 2b1– VO, (e) 2b2– VO, and (f) 2b3– VO. The gray and black spheres represent Si and O atoms, respectively.

Because defects can modify electronic states and then affect optical properties. Thus, the density of state (DOS) is calculated to describe how the defects influence the electronic properties. To characterize the optical property, the absorption coefficient is calculated, which can be obtained by the complex dielectric function ɛ (ω ) (ɛ (ω ) = ɛ 1 (ω ) + iɛ 2 (ω )). The absorption spectrum is described by the following equation:[42]

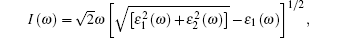
where ω is the frequency of light, and ɛ 1 (ω ) and ɛ 2 (ω ) are the real and imaginary parts of the complex dielectric constants, respectively.

3.Results and discussion
3.1.Structures

The calculated lattice parameters of the perfect α -quartz supercell are a = b = 10.0795  Å , c = 10.9558  Å , α = 89.5366° , β = 90.4634° , and γ = 120.835° . Compared with the experimental values, the GGA values have the deviation within 2.6% for the lattice parameters. As for the cell volume, the result obtained by GGA approximation is about 5.7% larger than the experimental data. Additionally, for the Si– O bond length in the intact α -quartz, our setting predicts lengths in a range of 1.618  Å – 1.630  Å compared with the experimental value of 1.61  Å .[43] Meanwhile, the previous calculations give the values of 1.623  Å – 1.631  Å .[13, 15]

When the oxygen vacancy (1– VO) is introduced into α -quartz, the Si– Si bond length at the vacancy is 2.463  Å , which is similar to the previous results of 2.50  Å [44] and 2.44  Å .[15] It is also consistent with the observed Si– Si separation at the relaxed oxygen vacancy ∼ 2.50  Å .[45] At the same time, the range of the Si– O bond lengths surrounding the vacancy extends to 1.633  Å – 1.642  Å . Table  1 gives the structural parameters of the oxygen vacancies, when the α -quartz has a higher VO concentration (oxygen divacancy), there is a further expansion in the Si– Si length compared with the length in the crystal with 1– VO, except for 2b2– VO (2.424  Å and 2.423  Å ), which can be found in Table  1. Especially, with the defect of 2a– VO, the atomic structure of the vacancies is quite different from the others’ , and the Si– O bonds are severely distorted. But the atomic structures of the two vacancies are similar to each other, as well as the other types of 2– VO. For the type of 2b3– VO, the two vacancies share the same atomic structure in the Si– Si and Si– O bonds. Moreover, our calculated Si– Si bond length, 2.467  Å , is close to the reported value of 2.46  Å .[15]

Table 1. Structural parameters of the oxygen vacancies for the configurations with oxygen divacancy, and the length bond is given in unit Å .

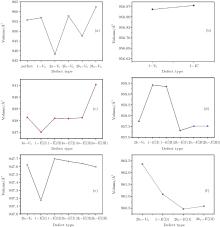
Fig.  2. Calculated volumes of α -quartz with various defects: (a) neutral VO(s), (b) 1– VO, and center, (c) 2a– VO and center, (d) 2b1– VO and center, (e) 2b2– VO and center, and (f) 2b3– VO and center.

The volumes of α -quartz structures with various defects are listed in Fig.  2. 1– VO enlarges the geometry of α -quartz with a value of 1.264  Å 3 as shown in Fig.  2(a). However, different types of 2– VO result in different volumes and geometries. 2b1– VO and 2b3– VO lead to a further expansion in the volume. Whereas the volume becomes smaller than the perfect crystal size, when the structure with 2a– VO or 2b2– VO. It indicates that the distribution of the two vacancies can affect the geometry of α -quartz.

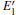
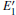
We can briefly analyze the effect of the center on the geometry of α -quartz in Figs.  2(b)– 2(f). From Fig.  2(b), we find that the center can hardly change the volume of α -quartz with 1– VO. When there are two point defects, the number of centers makes some differences, so does the position of the positive charge. It indicates that when α -quartz involves a higher defect concentration, the effect of center on the α -quartz geometry will become significant.

3.2.Density of states

3.2.1.Neutral oxygen vacancy

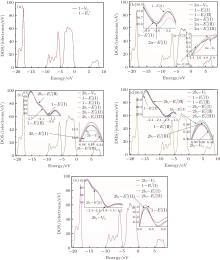
Figure  3 shows the calculated DOSs for the α -quartz with and without neutral oxygen vacancies. We can know that the band gap of the perfect α -quartz is 5.67  eV, which is smaller than the experimental values of 8.29  eV– 9.55  eV[46] and 8.9  eV.[47] But it is similar to the calculated values of 5.8  eV[15] and 5.7  eV.[16] As shown in Fig.  3, there are four distinct bands (three bands in the valence band and one band in the conduction band) in the DOS curve of the perfect α -quartz, and the highest occupied state (the maximum of valence band) is located near the Fermi level. Upon formation of the VO, the locations of the four bands evidently shift compared with those in the case of the intact crystal. Almost all of the bands move toward the lower energy level as described by Zhang et al.[15] In particular, the movement of the band in the conduction band results in the reduction of the band gap. Meanwhile, the peaks also decrease with the formation of VO. However, there is agreement in the positions of the DOS bands for the defective α -quartz, except for the model with 2a– VO. When the α -quartz has two adjacent VOs, further  movement occurs in all bands, especially in the DOSs in the conduction band. As a result, the band gap becomes narrower than those of other structures. The changes in the DOSs may be a result of the redistribution of the two electron charges that remains after the O atom has moved to the two neighboring Si atoms.

In the valence band, each of the calculated DOSs is lower than that of the undefected α -quartz. Moreover, the DOS bands (in the valence band) continually decrease as the number of defects increases. However, the DOSs for the models with 2– VO centers are higher than those with 1– VO at the edge of conduction band, except for the model with the 2b2– VO center. In addition, we find that different types of 2– VO centers exhibit minimal differences in the DOS of the valence band, and the 2b2– VO center exhibits a noticeable decrease. The similarity in the DOSs is also present in 2b1– VO and 2b3– VO as their curves almost completely overlap. The variations observed in the calculated DOSs are attributed to the electrons activated at various levels. On the basis of these results, we infer that the concentration and distribution of vacancies can sufficiently affect the electronic structure.

Fig.  3. The calculated DOSs for α -quartz without and with neutral oxygen vacancy/vacancies.

3.2.2. center

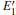
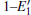
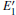
The DOSs of structures with centers are also calculated. The results are shown in Fig.  4. DOSs for the models with and 1– VO are in excellent agreement as illustrated in Fig.  4(a). It means that neither shifting a single VO defect into the center nor catching a hole or losing an electron (one of the Si atoms at the VO) will affect the electronic structure.

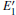
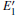
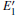
Some minor differences emerge in the two bands near the Fermi level (in the conduction band and at the edge of valence band), when the 2a– VO center is introduced into the α -quartz as shown in Fig.  4(b). However, the differences from the other valence bands are undetected. The undetected differences imply that the center can hardly affect the major of DOS, but the center has a great influence on the DOSs near the Fermi level. Furthermore, it suggests that the effect of catching a hole or losing an electron (an arbitrary Si atom in the VO center) is almost negligible, and the electronic excitation can easily happen. Similar phenomena also appear in the other systems as shown in Figs.  4(c)– 4(e). We can conclude that for the configuration with one or two centers, the behavior of the DOS is qualitatively similar to that of α -quartz with corresponding 2– VO center.

Fig.  4. DOSs of different configurations with center(s): (a) 1– VO, (b) 2a– VO, (c) 2b1– VO, (d) 2b2– VO, and (e) 2b3– VO.

3.3.Absorption spectrum

3.3.1.Neutral oxygen vacancy

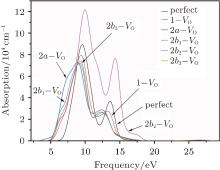
The absorption spectra for the related configurations with neutral VO(s) are displayed in Fig.  5. Notably, the absorption intensity, as well as the frequency where the peaks occur, decreases upon formation of the VO. Simultaneously, the optical absorption band widens compared with the shape of absorption spectrum curve for the perfect α -quartz. The changes indicate that the introduction of VO can remarkably influence the optical property of α -quartz. Once the two VOs appear, the absorption intensities are further reduced, except for the 2b2– VO type. The decrease observed in the absorption coefficient shows that the concentration of defects can affect the optical property of α -quartz. However, the absorption band widths of configurations with single VO and some types of 2– VO are still similar.

Fig.  5. Absorption spectra for the α -quartz without and with neutral oxygen vacancy/vacancies.

It should be emphasized that the influence of 2b2– VO on the absorption spectrum is profoundly different from those of the other types of defects. The 2b2– VO center results in a maximum absorption intensity that is considerably higher than those of other configurations, and the positions of the two peaks are at the lower energies. In addition, we can also notice that the 2b2– VO leads to the widest optical absorption band among the defective configurations. However, the lineshapes of the absorption spectrum for 2b1– VO and 2b3– VO are similar to each other, which is similar to the case of the corresponding DOSs. The dissimilarities and similarities reveal that the distribution of vacancies becomes more significant.

3.3.2. center

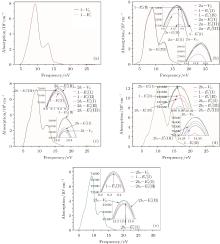
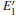
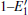
According to Fig.  6, the absorption spectrum for α -quartz with centers is similar to that from the model with the corresponding VO, just like the case of DOSs. And the absorption spectra are very close, including the absorption peaks and the frequencies where the peaks take place. Especially, the two absorption lines for α -quartz with and 1– VO coincide with each other as shown in Fig.  6(a). From Figs.  6(b)– 6(e), some differences can be seen in the absorption spectra, when there are two defects in α -quartz. However, the differences are minor enough. It suggests that shifting the neutral VO into the center will make very little effect on the optical properties of α -quartz.

Fig.  6. Absorption spectra for the α -quartz with centers: (a) 1– VO, (b) 2a– VO, (c) 2b1– VO, (d) 2b2– VO, and (e) 2b3– VO.

4.Summary and conclusions

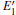
According to the calculations, the number of neutral VOs, as well as the type of 2– VO (2a– VO, 2b1– VO, 2b2– VO, and 2b3– VO), can affect the geometrical structrue of α -quartz. The presence of center does not significantly change the volume of α -quartz with 1– VO. However, when the higher defect concentration is involved in α -quartz, the influence of center becomes more significant.

There are evident variations in the positions of the four bands of the DOSs upon the formation of the VO center, almost all of them move toward the lower energy level. The movement of the band in the conduction band results in the reduction of the band gap. In addition, different types of 2– VO centers can lead to some differences in DOS, and the 2b2– VO center results in a noticeable decrease. However, a similarity is also present as the curves of the DOSs for 2b1– VO and 2b3– VO almost completely overlap. The above descriptions suggest that the concentration and distribution of oxygen vacancies can cause changes in the electronic structure of α -quartz. At the same time, the similarity, which is observed in the DOSs between the configurations with 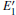center(s) and the corresponding 2– VO center, indicates that the presence of center can hardly affect the electronic structure.

Our calculations also show that the optical absorption band widens with the formation of the VO, and the absorption intensity becomes lower than that of the undefected α -quartz. The changes indicate that the introduction of VO can remarkably influence the optical properties of α -quartz. When the 2– VO center appears in the α -quartz, the dissimilarites and similarities are also reflected in the absorption spectra, similar to the case of DOSs. The results reveal that the concentration and distribution of neutral oxygen vacancies can influence the electronic structures and optical property of α -quartz.

Reference
1 Wang K P and Huang Y 2011 Chin. Phys. B 20 077401 DOI:10.1088/1674-1056/20/7/077401 [Cited within:1]
2 Wang H, Lin J J, He J Q, Liao Y L and Li S T 2013 Acta Phys. Sin. 62 226103 DOI:10.7498/aps.62.226103(in Chinese) [Cited within:1]
3 Zhou H B and Jin S 2013 Chin. Phys. B 22 076104 DOI:10.1088/1674-1056/22/7/076104 [Cited within:1]
4 Li F, Lu R F, Wu H P, Kan E J, Xiao C Y, Deng K M and Ellis D E 2013 Phys. Chem. Chem. Phys. 15 2692 DOI:10.1039/c2cp43350h [Cited within:1]
5 Liu Y, Liang P, Shu H B, Cao D, Dong Q M and Wang L 2014 Chin. Phys. B 23 067304 DOI:10.1088/1674-1056/23/6/067304 [Cited within:1]
6 Khan A, Rawat R S, Ahmad R and Shahid M A K 2013 Chin. Phys. B 22 127306 DOI:10.1088/1674-1056/22/12/127306 [Cited within:1]
7 Li R and Sun D H 2014 Acta Phys. Sin. 63 056101(in Chinese) DOI:10.7498/aps.63.056101 [Cited within:1]
8 Chen X B, Hien N T M, Yang I S, Lee D and Noh T W 2012 Chin. Phys. Lett. 29 126103 DOI:10.1088/0256-307X/29/12/126103 [Cited within:1]
9 Griscom D L and Friebele E 1986 Phys. Rev. B 34 7524 DOI:10.1103/PhysRevB.34.7524 [Cited within:1]
10 Kajihara K, Ikuta Y, Oto M, Hirano M, Skuja L and Hosono H 2004 Nucl. Instrum. Method Phys. Res. B 218 323 DOI:10.1016/j.nimb.2003.12.032 [Cited within:1]
11 Weil R A 1956 J. Appl. Phys. 27 1376 DOI:10.1063/1.1722267 [Cited within:1]
12 Silsbee R H 1961 J. Appl. Phys. 32 1459 DOI:10.1063/1.1728379 [Cited within:2]
13 Blöchl P E 2000 Phys. Rev. B 62 6158 DOI:10.1103/PhysRevB.62.6158 [Cited within:3]
14 Kuo C L and Hwang G S 2006 Phys. Rev. Lett. 97 066101 DOI:10.1103/PhysRevLett.97.066101 [Cited within:1]
15 Zhang G, Li X, Tung C H, Pey K L and Lo G Q 2008 Appl. Phys. Lett. 93 022901 DOI:10.1063/1.2957657 [Cited within:6]
16 Mao L F 2007 Microelectron. Reliab. 47 1213 DOI:10.1016/j.microrel.2006.09.027 [Cited within:2]
17 Nadimi E, Plänitz P, Öttking R, Schreiber M and Radehaus C 2010 IEEE Electron. Dev. Lett. 31 881 DOI:10.1109/LED.2010.2051013 [Cited within:3]
18 Rudra J K and Fowler W B 1987 Phys. Rev. B 35 8223 DOI:10.1103/PhysRevB.35.8223 [Cited within:2]
19 Lu Z Y, Nicklaw C J, Fleetwood D M, Schrimpf R D and Pantelides S T 2002 Phys. Rev. Lett. 89 285505 DOI:10.1103/PhysRevLett.89.285505 [Cited within:2]
20 Weeks R A and Nelson C M 1960 J. Am. Ceram. Soc. 43 399 DOI:10.1111/jace.1960.43.issue-8 [Cited within:1]
21 Roma G, Limoge Y and Baroni S 2001 Phys. Rev. Lett. 86 4564 DOI:10.1103/PhysRevLett.86.4564 [Cited within:1]
22 Song J, Corrales L R, Kresse G and Jónsson H 2001 Phys. Rev. B 64 134102 DOI:10.1103/PhysRevB.64.134102 [Cited within:1]
23 Van Ginhoven R M, Jónsson H, Peterson K, Dupuis M and Corrales L R 2003 J. Chem. Phys. 118 6582 DOI:10.1063/1.1559139 [Cited within:1]
24 Kang J, Kim Y H, Bang J and Chang K J 2008 Phys. Rev. B 77 195321 DOI:10.1103/PhysRevB.77.195321 [Cited within:3]
25 Marshall C D, Speth J A and Payne S A 1997 J. NonCryst. Solids 212 59 DOI:10.1016/S0022-3093(96)00606-0 [Cited within:1]
26 Mukhopadhyay S, Sushko P V, Stoneham A M and Shluger A L 2004 Phys. Rev. B 70 195203 DOI:10.1103/PhysRevB.70.195203 [Cited within:1]
27 Jani M G, Bossoli R B and Halliburton L E 1983 Phys. Rev. B 27 2285 DOI:10.1103/PhysRevB.27.2285 [Cited within:1]
28 Kalceff M A S and Phillips M R 1995 Phys. Rev. B 52 3122 DOI:10.1103/PhysRevB.52.3122 [Cited within:1]
29 Poindexter E H and Caplan P J 1988 J. Vac. Sci. Technol. A 6 1352 DOI:10.1116/1.575701 [Cited within:1]
30 Lin G R, Lin C J, Lin C K, Chou L J and Chueh Y L 2005 J. Appl. Phys. 97 094306 DOI:10.1063/1.1886274 [Cited within:1]
31 Uchino T and Yoko T 2006 Phys. Rev. B 74 125203 DOI:10.1103/PhysRevB.74.125203 [Cited within:1]
32 Lenahan P M and Dressendorfer P V 1984 Appl. Phys. Lett. 44 96 DOI:10.1063/1.94566 [Cited within:1]
33 Chadi D J 2003 Appl. Phys. Lett. 83 437 DOI:10.1063/1.1592003 [Cited within:1]
34 Carbonaro C M, Fiorentini V and Bernardini F 2001 Phys. Rev. Lett. 86 3064 DOI:10.1103/PhysRevLett.86.3064 [Cited within:]
35 Shi S, Tanaka S and Kohyama M 2007 Phys. Rev. B 76 075431 DOI:10.1103/PhysRevB.76.075431 [Cited within:1]
36 Tang Y, Zhang H, Cui L, Ouyang C, Shi S, Tang W and Li H 2010 Phys. Rev. B 82 125104 DOI:10.1103/PhysRevB.82.125104 [Cited within:2]
37 Ouyang C, Du Y, Shi S and Lei M 2009 Phys. Lett. A 373 2796 DOI:10.1016/j.physleta.2009.05.071 [Cited within:1]
38 Shi S, Lu P, Liu Z, Qi Y, Hector L GJr, Li H and Harris S J 2012 J. Am. Chem. Soc. 134 15476 DOI:10.1021/ja305366r [Cited within:1]
39 Ghiorso M S, Carmichael I S E and Moret L K 1979 Contrib. Mineral. Petrol. 68 307 DOI:10.1007/BF00371553 [Cited within:1]
40 Vand erbilt D 1990 Phys. Rev. B 41 7892 DOI:10.1103/PhysRevB.41.7892 [Cited within:1]
41 Segall M D, Lindan P J D, Probert M J, Pickard C J, Hasnip P J, Clark S J and Payne M C 2002 J. Phys. : Condens. Matter 14 2717 DOI:10.1088/0953-8984/14/11/301 [Cited within:1]
42 Okoye C M I 2003 J. Phys. : Condens. Matter 15 5945 and the references therein DOI:10.1088/0953-8984/15/35/3042003 [Cited within:1]
43 Wyckoff R W G 1965 Crystal Structures New York InterscienceVol.  1, 321 [Cited within:1]
44 Sokolov V O and Sulimov V B 1986 Phys. Status Solidi B 135 369 DOI:10.1002/(ISSN)1521-3951 [Cited within:1]
45 StevensKalceff M A 2009 Mineral. Mag. 73 585 DOI:10.1180/minmag.2009.073.4.585 [Cited within:1]
46 Tan G L, Lemon M F, Jones D J and French R H 2005 Phys. Rev. B 72 205117 DOI:10.1103/PhysRevB.72.205117 [Cited within:1]
47 Pacchioni G and Ierano G 1998 Phys. Rev. B 57 818 DOI:10.1103/PhysRevB.57.818 [Cited within:1]