Cite this Article
Song Zhen, Liu Xiao-Lang, He Li-Zhu, Xia Zhi-Guo, Liu Quan-Lin†. Complementary method to locate atomic coordinates by combined searching method of structure-sensitive indexes based on bond valence method. Chinese Physics B, 24(10): 106101  
Permissions
Complementary method to locate atomic coordinates by combined searching method of structure-sensitive indexes based on bond valence method
Song Zhen, Liu Xiao-Lang, He Li-Zhu, Xia Zhi-Guo, Liu Quan-Lin†
School of Materials Science and Engineering, University of Science and Technology Beijing, Beijing 100083, China

†Corresponding author. E-mail: qlliu@ustb.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 51272027).

Abstract

Bond valence method illustrates the relation between valence and length of a particular bond type. This theory has been used to predict structure information, but the effect is very limited. In this paper, two indexes, i.e., global instability index (GII) and bond strain index (BSI), are adopted as a judgment of a search-match program for prediction. The results show that with GII and BSI combined as judgment, the predicted atom positions are very close to real ones. The mechanism and validity of this searching program are also discussed. The GII & BSI distribution contour map reveals that the predicted function is a reflection of exponential feature of bond valence formula. This combined searching method may be integrated with other structure-determination method, and may be helpful in refining and testifying light atom positions.

PACS: 61.05.–a; 61.50.Ah; 61.43.Bn
Keyword: bond valence method; atomic coordinate prediction; combined searching
1.Introduction

X-ray diffraction reveals the fine structure of crystal. With the improvement in machinery manufacturing, it is feasible to precisely determine structure information, [1] such as cell parameters, atomic coordinates, bond lengths, etc. This leads to a revolution in solid state science. Bond valence method (BVM) is one of the theories that benefits from precise x-ray measurements. Brown and Shannon[2] adjusted Pauling’ s second rule[3] by introducing bond length and empirical constant of specific cation– anion pair. Until then, this new method had been found to have its value by solving a series of problems.[4– 7] BVM builds up a bridge between the measured quantity (bond length) and theoretical quantity (bond valence). Is it possible to predict the unknown bond length by a limited knowledge of bond valence? Researchers have made many attempts to predict the unknown bond lengths. For example, Brown used BVM to predict bond lengths in CaMgSi2O6, K2S5O16, Na2B4O7, and Na2PO3F, etc., and obtained satisfactory results.[8] O’ Keeffe was successful in predicting the cases of Li2SiO3 and Li2GeO3, etc.[9] Rutherford developed the computing algebra with the example of KVO3, etc.[10, 11] However, as pointed out by O’ Keeffe, this kind of method had limitations and was far from being perfect.[9] First, the predicting method is based on solutions of network equations, which are composed of valence sum rule and loop valence rule. Under the requirements of valence sum rule, the sum of bond valences of a cation is equal to its atomic valence. This rule, however, does not usually hold for real structures; moreover, the difference gives important information about crystal chemistry.[12] Second, the setup of network equations are based on the configuration of a given bond graph, in which all the bonds that belong to a specific pair of cation– anion are treated equally. Therefore, they have the same length and valence, which is not the case for cations occupying low symmetry positions.

Apart from direct calculation, introducing evaluation index based on BVM is also practical for prediction. Evaluation indexes of possible structures could be calculated and compared in order to pick out the most suitable one. One of the evaluation indexes is global instability index (GII), which measures the deviation between the sum of bond valence of an ion and its atomic valence. It is used to judge the stability of structure. Structures with too large GIIs may not exist while those with small GIIs are stable.[5] With this property, Kroll et al.[13] employed GII together with distant-least-squares method for prediction. However, as will be shown in the following section, GII alone sometimes does not work well and should be used together with other constraints.

In this work, bond strain index (BSI) is introduced for prediction. This index deals with each single bond and measures the deviation between experimental and theoretical bond lengths. Two garnet-type structures are adopted to show that the combination of GII and BSI could give better prediction than GII alone. The mechanisms of the two indexes are also discussed.

2.Method

For uniformity, all the equations come from Brown’ s definitions.[14]

Bond valence is defined as

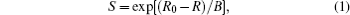
where R is the bond length while R0 and B are empirical constants.

The mathematical expressions of GII and BSI are

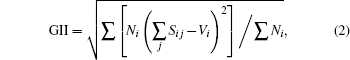
where Sij is the j-th bond valence of atom i, the summation goes over all the bonds connecting that atom, Vi is the atomic valence of atom i, and Ni is the multiplicity of the site;

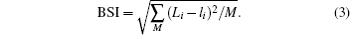
Here, the upper-case Li in BSI expression represents the experimental bond valence, which is determined by x-ray diffraction (XRD) determination, the lower-case li is theoretical bond valence, which is obtained by solving network equations with bond valence wizard[15] software, and M is the number of all the bonds in the unit cell.

The garnet-type and are taken for example, and their crystallographic information is listed in Table 1.[16, 17] In both structures, most of the cations occupy high symmetry positions; therefore, their fractional coordinates are fixed. However, the oxygen anions occupy general equivalent positions, with fractional coordinates unfixed and usually obtained by XRD determination. In this work, they are treated as prediction objects to be solved by BVM.

Table 1. Crystallographic information of Y3Al5O12 and Y2O3.

The prediction algorithm is given as follows: oxygen fractional coordinates (x, y, z) are set as three-dimensional free parameters. They will change, separately, in in a range of (0, 1). For each set of (x, y, z) values, the corresponding BSI and GII are calculated and compared with the former ones. The smaller one as well as (x, y, z) values will be stored. When the iteration finishes, the minimal 5 groups of data will be output to a text file. The code is written in FORTRAN and can be found in supplemental materials.

The algorithm is then optimized. The whole iteration process is divided into four loops. In the first loop, (x, y, z) will change from 0 to 1 in steps of 0.01. This will take one million times calculations (100 × 100 × 100). At the end of the first loop, the (x, y, z) values that lead to the smallest GII and BSI will be stored as (x1, y1, z1). In the second loop, the limits for x, y, and z will become [x1 − 0.05, x1 + 0.05], [y1 − 0.05, y1 + 0.05], and [z1 − 0.05, z1 + 0.05] and the step becomes 0.001. The second loop will take another one million times calculations and the optimum (x2, y2, z2) will be used to define the limits in the third loop, i.e. [x2 − 0.005, x2 + 0.005], [y2 − 0.005, y2 + 0.005], and [z2 − 0.005, z2 + 0.005]. The third and fourth loops are iterated in steps of 0.0001 and 0.00001 respectively. This algorithm will save CPU time because it takes four million times calculations in total, whereas iteration from 0 to 1 in steps of 0.00001 will take 1015 times calculations.

The case of Y2O3 is similar to Y3Al5O12 except that for Y2O3 an x fractional coordinate of yttrium should also be iterated. This will increase the total number of calculations, but the program is almost the same.

3.Results and discussion
3.1.Prediction of oxygen coordinates in Y3Al5O12 using GII and GII & BSI

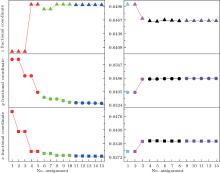
The first searching program using GII only is designed to find (x, y, z), of which the GII can reach a minimum. The second program is modified by introducing BSI as another constraint together with GII. It is designed to find those (x, y, z) values, of which the BSI can reach a minimum while GII is no more than the stability limit. Commonly, the limit value is set to be 0.2.[5, 14] For each loop, the output text file records (x, y, z) values which give the minimal 5 GIIs or 5 BSIs. Those files are included in the supplemental materials, and the results are plotted in Fig. 1. The trend of data shows that with the increase of data resolution, all of the three coordinates converge to certain values which are then treated as predicted coordinates. The results are listed in Table 2. It can be seen that the oxygen coordinates predicted by GII & BSI are much closer to real ones than those predicted by GII only.

Fig. 1. Trends of (x, y, z) values at different loops. For each loop, 5 sets of data which give the minimum 5 GIIs or 5 BSIs are recorded. The square, circle, and triangle symbols denote x, y, and z fractional coordinates, respectively. Symbols of different color belong to different loops. Left: the judgement statement uses GII only. Right: the judgement statement uses GII & BSI. In the 1st and 2nd loops, only a few data sets meet the requirement (GII ≤ 0.2).

Table 2. Comparison of predictions with real atomic fractional coordinates in Y3Al5O12.

The obtained (x, y, z) coordinates are used to calculate the corresponding bond lengths (Table 3). It is obvious that bond lengths predicted by GII only are similar to theoretical bond lengths, which are obtained under the premise of zero GII (atomic valence is assigned equally to the connecting bonds). During the first searching program, the obtained GIIs are closely approaching zero, which confirms the above conclusion. Therefore, the weakness of prediction method using GII only is that it focuses only on arithmetic requirements but ignores crystallographic limitations. Because network equations cannot distinguish bonds of different lengths, the theoretical bonds under the same type are all equal. In this case, the predicted bond lengths of Al1– O1 and Al2– O1 are exactly the same as theoretical bond lengths. This is due to the equal bond lengths in Al– O octahedron (Al1) and tetrahedron (Al2), respectively. However, for the case that theoretical Y– O bonds are not equal, the real Y– O bonds can be divided into two groups by lengths. In order to obtain the minimal GII, half of the predicted Y– O bonds are made shorter and the other half longer so that the summation of larger and smaller bond valences predicted will be the atomic valence (+ 3). However, the shorter (2.2378 Å ) and longer (2.6210 Å ) predicted bond lengths stray far from real ones and will result in a larger BSI. Therefore, introducing BSI as another constraint is very necessary. It can be concluded from Table 3 that the bond lengths predicted by using GII & BSI give a good approximation to real ones. This means that the GII & BSI combined searching method is more effective than using GII only.

Table 3. Comparison among theoretical bond length (in unit Å ), bond length (Å ) predicted by GII only/GII & BSI, and real bond length (Å ) in Y 3Al5O12.

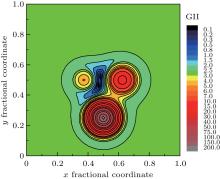
It is very interesting to investigate the GII or BSI distribution within a selected ‘ oxygen polyhedron’ — oxygen atom lies in the center whereas cations in the vertexes. The fractional coordinates of those atoms are transformed to crystal coordinates under symmetry operation. For example, the corresponding symmetry operation for oxygen atom is 0.5− x, 0.5− y, 1.5− z, and the crystal coordinates of real oxygen now turns into (0.4671, 0.4504, 0.8514). Symmetry operations and crystal coordinates for other atoms could be found in supplemental materials. For better visualization, the three-dimensional (3D) distribution is sliced at different Z values. The program is then modified by removing the judgment statement in order to record GII or BSI values of (x, y, z), with x, y varying in steps of 0.001 and z fixed at certain values. If the step is reduced further, the output file will be of gigabytes and difficult to manipulate. The data in steps of 0.001 are precise enough for qualitative description. The slice of GII distribution contour map at Z = 0.851 is selected as typical representation as shown in Fig. 2. The basic exponential formula of bond valence is reflected — as oxygen atom moves to the cations closer and closer, the bond valence grows dramatically, so the GII will have an exaggeratedly large value, especially in the central position of cations; if oxygen atom jumps out of the polyhedron and moves far away, the bond valence will approach zero, and GII will be stabilized in a relatively narrow range. This plot could thus be interpreted as the dynamical representation of the searching program. The target position will not wander across the plain outside the oxygen polyhedron, nor the plateau of cation atoms. It falls down naturally into the valley inside the oxygen polyhedron.

Fig. 2. Slice of ’ oxygen polyhedron’ GII distribution contour map at Z = 0.851.

Figure 3 shows the enlargement of contour areas with GII no more than 2.0 in Fig. 2. And for the contour of GII = 0.2, the corresponding BSI contours are overlaid. The positions of minimal GII, minimal BSI at this slice are indicated together with real oxygen atom position. The position of minimal GII is still far away from real oxygen position. Only under the guide of BSI distribution, will the target position slide into the minimal BSI, which nearly coincides with real oxygen position. Therefore, it can be concluded that the prediction mechanism of GII & BSI is based on the self-consistency of bond valence theory, and the satisfactory searching result based on GII & BSI is not just a coincidence but logical outcome due to the exponential relation between valence and length of a certain bond type.

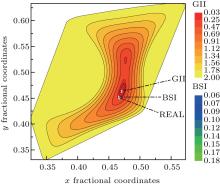Fig. 3. Magnified contour areas with GII no more than 2.0 in Fig. 2. The small overlaid area is the BSI contours with GII no more than 0.2. The three triangle symbols represent positions of minimal GII, minimal BSI, and real oxygen atom as indicated.

3.2.Prediction of atomic coordinates in Y2O3 using GII & BSI

According to the above discussion, the searching program of Y2O3 is thus based on GII & BSI combined method. In this case, however, four coordinates need to be searched, which will increase the total number of calculations to 400 million times. The whole process is similar to the case of Y 3Al5O12, of which the details are not given here any more. The results are shown in Table 4. The fractional coordinates predicted are also very close to the real coordinates.

Table 4. Comparison between predicted and real atomic fractional coordinates in Y2O3.
3.3.Limitations and prospect

The combined GII & BSI searching method is inherently an enumerate-judge iteration program. It cannot make ab-initio calculations, and relies on atom positions already resolved. With more unknown atom positions, the program will go slowly for more calculations. The combined searching method overcomes the weakness of previous prediction methods based on bond valence theory, and can give satisfactory results. It can be coded as an auxiliary program working together with other structure-solving program, and also used to refine and testify light atom positions in complex structures.

4.Conclusions

The prediction function of bond valence method is explored by introducing GII and BSI as judgement statement in a combined searching program. The results show that GII together with BSI works better than GII alone. With the analysis of bond lengths it can be found that the judgement statement using GII only will lead to violations of crystallographic rules. The GII or BSI distribution contour map slices are also investigated. This reveals the dynamical process of the searching program and makes it clear that the exponential relation between valence and length is the core component that can give satisfactory prediction results. The combined searching program may be recoded to assist other structure-determination program, and it will be helpful in recognizing and refining the light atoms.

Reference
1 Liu S J, Peng T J, Song Z, Bian L, Song G B and Liu Q L 2014 Chin. Phys. B 23 048106 DOI:10.1088/1674-1056/23/4/048106 [Cited within:1]
2 Brown I D and Shannon R D 1973 Acta Crystallogr. Sect. A: Found. Crystallogr. 29 266 [Cited within:1]
3 Pauling L 1929 J. Am. Chem. Soc. 51 1010 DOI:10.1021/ja01379a006 [Cited within:1]
4 Thomas N 1989 Ferroelectrics 100 77 DOI:10.1080/00150198908007902 [Cited within:1]
5 Salinas-Sanchez A, Garcia-Munoz J L, Rodriguez-Carvajal J, Saez-Puche R and Martinez J L 1992 J. Solid State Chem. 100 201 DOI:10.1016/0022-4596(92)90094-C [Cited within:2]
6 Rao G H, Bärner K and Brown I D 1998 J. Phys. : Condens. Matter 10 757 DOI:10.1088/0953-8984/10/48/001 [Cited within:1]
7 Hunter B, Howard C and Kim D J 1999 J. Solid State Chem. 146 363 DOI:10.1006/jssc.1999.8363 [Cited within:1]
8 Brown I D 1977 Acta Crystallogr. Sect. B: Struct. Sci. 33 1305 DOI:10.1107/S0567740877005998 [Cited within:1]
9 [Cited within:2]
10 Rutherford J S 1990 Acta Crystallogr. Sect. B: Struct. Sci. 46 289 DOI:10.1107/S0108768189013297 [Cited within:1]
11 Rutherford J S 1998 Acta Crystallogr. Sect. B: Struct. Sci. 54 204 DOI:10.1107/S0108768197012809 [Cited within:1]
12 Roulhac P L and Palenik G J 2003 Inorg. Chem. 42 118 DOI:10.1021/ic025980y [Cited within:1]
13 Kroll H, Maurer H, Stöckelmann D, Beckers W, Fulst J, Krüemann R, Stutenbäumer T and Zingel A 1992 Z Kristallogr 199 49 DOI:10.1524/zkri.1992.199.1-2.49 [Cited within:1]
14 Brown I D 2002 The chemical bond in inorganic chemistry: the bond valence model New York Oxford University Press 166 167 [Cited within:2]
15 Orlov I, Popov K and Urusov V 2002 Found. Phys. Lett. 15 575 DOI:10.1007/BF02701389 [Cited within:1]
16 Carda J, Tena M A, Monros G, Esteve V, Reventos M M and Amigo J M 1994 Cryst. Res. Technol. 29 387 DOI:10.1002/(ISSN)1521-4079 [Cited within:1]
17 Santos C, Strecker K, Suzuki P A, Kycia S, Silva O M M and Silva C R M 2005 Mater. Res. Bull. 40 1094 DOI:10.1016/j.materresbull.2005.03.017 [Cited within:1]