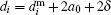
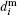
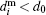
If a deviation of a nanoparticle shape from a spherical one has isotropic probability distribution then one could consider particles as hard spheres.^[56] The i-th particle hydrodynamical diameter consists of a ferromagnetic core diameter , a nonmagnetic surface layer thickness which equals a lattice constant a₀ of a respective bulk crystalline material, and a stabilizing surfactant layer thickness δ .^{[56, 57]} We will consider only single-domain particles with , ^[58] where the single-domain particle size threshold is d₀ < 0.5 μ m. ^{[59– 61]} A stabilizing surfactant molecules surface density N_S on a particle determines a rate of its coating and impacts on the FF stabilization.^[56]

The Rayleigh dissipation function of an N particles system includes each particle degrees of freedom 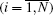: center of mass spatial coordinates r_i, Euler angles of a particle rotation, and a magnetic moment m_i where | m_i| = const. A particle potential energy depends on its Euler angles implicitly through an angle θ _i between m_i and a particle easy magnetization axis unit vector n_i.^[57]

The total force acting on the i-th nanoparticle is given by:

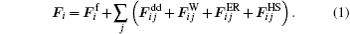
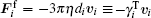
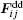
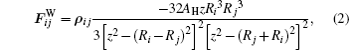
Assuming the limit of low Reynolds number, the viscous friction force is given by the Stokes’ law where η is a carrier liquid dynamic viscosity and v_i is the i-th particle velocity. The is a dipole– dipole interaction force.^{[14, 29, 57]} The van der Waals’ interaction energy between spherical bodies is given in Ref. [62]. Its differentiation yields the force:

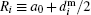
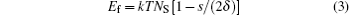
where A_H is the Hamaker constant; a radius ; a distance z = | r_i − r_j| ; and its dimensionless value ρ _ij = (r_i − r_j) /z. The energy density of entropic repulsion^[63] of two surfaces:

after an integration over surfaces of two particles with different radii takes the form (at z ≤ R_i + R_j + 2δ ):

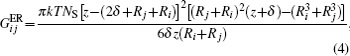
where k is the Boltzmann constant; T is a thermodynamic temperature; s is a distance between surfaces; δ is a surfactant molecule length. In the case of particles of the same radii, the closed-form expression equation (4) differs from the well-known logarithmic one.^{[63, 64]} However, these dependencies are numerically close to each other with the tolerance ∼ 20% for particles with diameter 10 nm. Existing experimental results cannot justify these expressions difference. The comparison of the derivation procedures will be published separately.

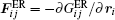
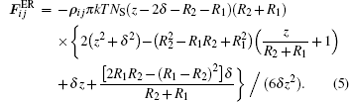
The corresponding force is given by

The hard-sphere model^[26] force is given by the following expression:

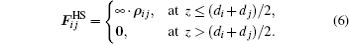
The total effective torque acting on the i-th particle is determined by a viscous rotational friction, a particle anisotropy, the applied external magnetic field B₀ value, and a dipole– dipole interaction field:^{[29, 52, 57]}

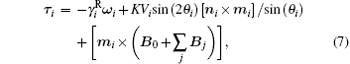
where 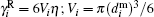is the i-th particle magnetic core volume; K is a particle magnetic anisotropy constant; the ω _i is the i-th particle self-rotation angular velocity; B_j is a magnetic field created by the j-th particle magnetic moment in the geometric center of the i-th particle. All types of magnetic anisotropies should be taken into account: a magnetocrystalline anisotropy, ^[65] a shape anisotropy (demagnetization tensor), ^[66] an anisotropy of surface, ^[67] etc.

In scope of the continuum solvation approximation of not very dense solutions, the Brownian translational and rotational particle motion is described by the Langevin equations with the hydrodynamic-originated Langevin parameters:^{[29, 40, 52, 68, 69]}

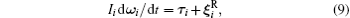
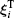
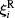
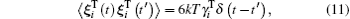
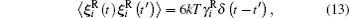
where M_i and I_i are the i-th particle mass and moment of inertia respectively; t is a time; and are random force and torque respectively, which are usually modelized by Gaussian noise:^{[29, 40, 69, 70]}

where δ (t) is the Dirac delta.

It is important to note that original Langevin equations were supplemented by particles interaction forces (1) and torques (7). This supplementation has been considered as an obvious and intuitive step which had been made in scope of the molecular dynamics simulation-based research programs.^{[29, 40, 52]} However, it still should be exactly theoretically justified in general case of the Brownian particle motion. This statement is in need of further research.

A rotation of a magnetic moment inside a particle is described by the Landau– Lifshitz– Gilbert equation with the attempt time t₀ = M_s/2α γ K where M_s is a saturation magnetization; α is a damping factor; γ is an electron gyromagnetic ratio.^[57] The simultaneous Brownian dynamics of a magnetic moment and a particle has been investigated in Ref. [71].

All parameters of the present simulation correspond to the specific experiment.^{[30, 31, 72]} The considered FF consists of the magnetite nanoparticles suspended in the kerosene carrier liquid. The stabilizing surfactant is the oleic acid (δ = 2 nm ^[56]). The particles diameter distribution was determined experimentally.^[72] The mean diameter is d̅ = 11.5 nm. The magnetite lattice parameter a₀ ≈ 0.8397 nm corresponds to the cubic spinel structure with the space group Fd3m (above the Verwey temperature).^{[73, 74]} However, this parameter is approximate because only 10% of particles have a crystal structure. This conclusion was made based on a dark field electron microscopy measurements.^[72] The simulation initial condition is a random close packing^[75] (cf. Ref. [33]) of particles positions and random magnetic moments directions. The external magnetic field is uniform. Dielectric properties of the surfactant layer are generally similar to those of the carrier liquid.^[33] Hence, the Hamaker constant of a magnetite is A_H = 4 · 10^{− 20} J.^[33]

A required step of a dense phase emergence is an original phase nucleus forming. Consequently, a phase diagram of a nucleus is close to a phase diagram of a bulk FF phase. Only the nucleus aggregate will be considered in this simulation. Hence, a number of particles N should be minimal but not less some threshold where a phase diagram start significant changes depending on the N: a transition from a bulk phenomenon to a surface one. Number N ∼ 100 has been selected for the polydisperse FF with a lognormal distribution.

The magnetic moment precession attempt (damping) time order of magnitude is τ ₀ ∼ 10^{− 10} s– 10^{− 9} s.^[56] In the case of particles d_i ≤ d̅ , the Né el relaxation time τ _N and the Brownian relaxation time τ _B relates as:^{[56, 63]}

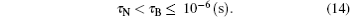
Most part of the range 0 < d ≤ d̅ corresponds to the relation τ _N ≪ τ ₀. In this case both the Né el relaxation flip and a magnetic moment dynamics should be considered. The Brownian rotation is a much slower process. A particle rotation does not impact on a magnetic configuration and a free energy of the phase.

The relation is opposite for the larger particles d_i > d̅ :^[57]

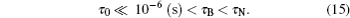
Here, a magnetic moment alignment with an effective field can be modeled as instant. The magnetic moment rotates the particle through anisotropy forces. We suppose that the high enough anisotropy energy KV gradient leads to the model with the magnetic moment “ frozen” into the particle. The vector m_i is followed by the vector n_i:

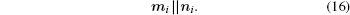
The saturated surface density of a number of oleic acid molecules in a particle coating is 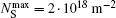.^[56] Depending on an FF preparation recipe variation (an order of mixing/heating of different components, ^[72] etc.), the coating rate can differ. A classical well-stabilized FF usually has k_c ∼ 50% which blocks the particles aggregation during durable timeframes (years) due to the free energy barrier 15 kT– 25 kT (Fig. 1(a)).^[56] The Brownian motion kinetic energy ∼ 1 kT is not enough to overpass the barrier. Only larger particles form aggregates, ^{[10, 14]} which corresponds to the potential well at the l ≈ 0.5 (Fig. 1(a)). In the experimental research^[31] the k_c value had been reduced, which leads to the dense phase (drop-like aggregates) emergence (Fig. 1(b)). Same mesoscopic organization control has been reported in Ref. [76]. The value k_c = 5% has been selected for the present simulation. The calculation of an entropy and the corresponding free energy F by the Eyring’ s free volume theory^[77] based algorithm^[33] has been made for the system of particles used in the present simulation (Fig. 2). The potential well required for the dense phase emergence is 2 kT– 4.5 kT or more.^[24] An equilibrium state corresponds to the dense phase of such FF. A particles contact leads to an infinite negative potential energy of the van der Waals interaction. The entropic repulsion cannot counteract. However, particles mutual attraction is reversible due to an existence of a minimal distance between their surfaces s_min < δ (Fig. 1(b)). The value s_min = 0.5_a0 nm has been selected as a half of a cell constant which qualitatively reflects restrictions of the Hamaker theory-approximated consideration of spherical particles as a continuous body (2) in the case of distances comparable to atomic scale. It corresponds to surface structure peculiarities, a nanoparticle quasicrystalline structure, etc. On the other hand, the value s_min corresponds to an order of magnitude of two oleic acid molecular widths. This additional to the entropic repulsion (4) stabilized “ buffer” role of the surfactant molecule has been discussed in Ref. [56].

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Potential energy dependence on the dimensionless distance between two identical magnetite particles surfaces l = 2s / d. Different particles diameters d are specified. (a) Coating rate by the oleic acid: kc = 50% and (b) coating rate by the oleic acid: kc = 5%.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Average free energy of the particle in the aggregate with 100 particles with random positions which fits to the density. The dependence on the volume fraction of the ferrofluid dispersed phase is shown. Coating rate by the oleic acid is kc = 5%. Different particles d diameters are specified.

The finite-difference Euler scheme is based on the original method.^[14] The only changes will be described below. Algorithm details of the present method can be accessed and contributed in the open-source project “ Ferrofluid Aggregates Nano Simulator” .^[78] The Verlet type of a finite-difference method^[79] is in need of further method improvement.

A random particle translation and rotation is considered by means of the viscous limit approximation^{[57, 69, 80]} which restricts a time tolerance corresponding to a finite-difference scheme time step:

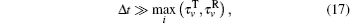
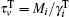
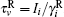
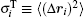
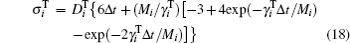
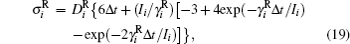
where and . Consequently, an inertial term of the motion equations (8) and (9) can be neglected.^[69] After the integration by the technique^[69] taking into account Eqs. (10)– (13) one can obtain particle random motion dispersions and respectively (cf. Ref. [29]):

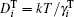
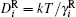
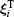
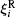
where vector Δ φ _i defines the i-th particle rotation (an axis-angle representation; dφ _i/dt ≡ ω _i); diffusion coefficients are given by the Stokes– Einstein translational and rotational equations: and respectively. The corresponding normal distribution (Wiener process of Brownian motion) of and is calculated by the Mersenne twister algorithm.^[81]

The magnetic moment Né el (14) and Brownian (15) relaxation types correspond to different calculation algorithms of the magnetic moment motion which were distinguished by a particle diameter criterion. In the case of the Né el type and Δ t ≫ τ _N, the magnetic moment was aligned with the total magnetic field direction in the i-th particle center r_i at each simulation step. In the case of the Brownian type, the rotational motion (9) of the particle with the “ frozen” (16) magnetic moment is calculated.

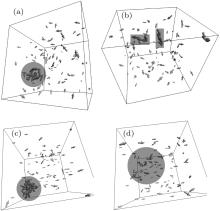
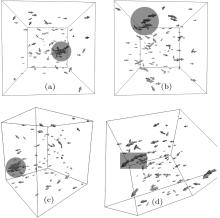
An evolution of the initial random close packing structure (Fig. 3) to the thermodynamically equilibrium state was calculated. In the case of the dense phase (the nucleus equilibration at the end of the simulation), after a stabilization period t_s = t_s (H₀, T), a total moment of inertia of the system I_tot is not changing except its random fluctuations (Fig. 4). This statement has been validated up to t = 0.2 s for all obtained dense phases. The resulted structures are shown in Figs. 5 and 6. In order to distinguish a diluted and dense phase, simpler and similar approach comparing to a conventional correlation function is used. A one-dimensional chain^{[13– 16]} is defined in the present simulation as a cluster of particles which satisfies the condition | ρ _{i(i + 1)}| ≤ d_i + d_{i + 1} where the i-th and (i + 1)-th particles are neighbors in the chain. Here, each particle can have only 1 or 2 neighbors. A circle is a particular case of such a chain. A set of separated arbitrary length one-dimensional chains is being considered as a diluted phase. If stabilized equilibrium state (see Fig. 4) corresponds to at least single particle with the number of neighbors larger than 2 then the more complex dense structure is formed. This phase is defined as a dense phase by definition.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Initial conditions: perspective projection. A space is limited by the cubic vessel with the edge length L = 0.3 μ m.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Total moment of inertia time dependence at the conditions: the temperature T = 25 ° C and the external field H0 = 0 Oe (1 Oe = 79.5775 A · m− 1). The obtained approximated value of the dense phase stabilization period is ts ∼ 5 ms.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Resulted thermodynamically equilibrium structures: perspective projections (area with largest particles is highlighted); L = 0.3 μ m. A size of volumetric arrows is proportional to a geometrical size of the corresponding nanoparticle for an illustrative purpose only. (a) H0 = 0 Oe and T = 50 ° C, (b) H0 = 0 Oe and T = 75 ° C, (c) H0 = 200 Oe and T = 35 ° C, (d) H0 = 200 Oe and T = 55 ° C,

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Resulted thermodynamically equilibrium structures (continue). (a) H0 = 400 Oe and T = 15 ° C, (b) H0 = 400 Oe and T = 20 ° C, (c) H0 = 800 Oe and T = 0 ° C, (d) H0 = 800 Oe and T = 10 ° C,

The phase diagram is obtained based on an analysis of the resulted structures (Figs. 5 and 6) using a bisection method for the definition of the phase transition temperature T_t. The binodal curve of the phase diagram (Fig. 7) corresponds to the experimental results in terms of the trend and the T_t approximate value in the case of a comparison of temperature values in Kelvins.^{[30, 31]} This trend has been observed experimentally only starting from the second cycle of the system heating/cooling. The first heating corresponds to the trend weaker than experimental errors and noises.^{[30, 31]} It can be explained by the assumption that the initial experimental sample state does not correspond to the initial conditions of the simulation, i.e., the aggregate with the random close packing^[75] of a polydisperse set of particles (Fig. 3). Indeed, a final equilibrium state of a non-stabilized FF is a set of primary aggregates which consist of large particles only (diameter ).^[14] Hence, the first heating is required in order to produce the metastable random close packing structure which is kept within several heating/cooling cycles. The large FF aggregate transforms to the primary aggregates state after durable timeframes which require the first heating/cooling cycle again.

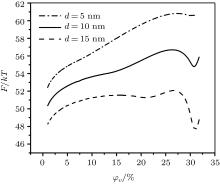
The descending binodal curve (Fig. 7) contradicts to some theoretical investigations where this dependence is ascending.^{[10, 24, 25]} As it is stated at the beginning, a contradiction between these theory conclusions and simulation reports is deeper: even a conceptual possibility of an FF LG transition emergence is being discussed among different research programs.^[9] Mean-field and statistical models are not justified in the case of a large coupling constant and/or large concentration of FF nanoparticles.^[29] Oppositely, they are justified in the case of a high-temperature and/or a diluted phase FF where a correlation in orientations of magnetic moments is small.^[26] The latter case corresponds to a modeling of an FF by the classical Lennard-Jones (LJ) fluid and short-range order, ^{[26, 82]} which excludes the possibility of an emergence of particles complex long-range ordered structures such as linear chains, rings, tubes, etc.^{[14, 15]} However, it is well established^[9] that an equilibrium FF phase microstructure consists of a distribution of chains, rings or more complex structures of different lengths. Hence, a real FF dense phase should be modeled by a liquid crystal-like microstructure rather than by the classical LJ fluid. However, the LJ fluid is a suitable model for conditions which break the long-range ordered structures through an entropy increase and a predominance of the Brownian motion: a high temperature, a low particles concentration (leading to a structures “ evaporation” ), a major particle coating, etc. In this case a potential energy summand of an FF free energy^[33] is suppressed by an entropic summand; the free energy local minimum takes place only for large particles (the φ _V < 25%– 30% area in Fig. 2). This is why an LG transition in the framework of the LJ ferrofluid model is possible only in bi-disperse^[24] or polydisperse FF thermodynamic theories.

Fig. 7.

	Figure Option ViewDownloadNew Window
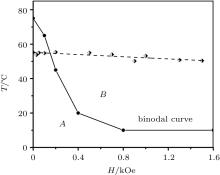	Fig. 7. Ferrofluid nucleus phase diagram: region “ A” : the aggregated phase and the diluted phase coexistence in the vessel volume; region “ B” : the diluted superparamagnetic phase only. The simulation results (circles) form a binodal curve. The experimental results[31] (diamonds) are given for a comparison.

The LJ-like ferrofluid theories correspond to the following idealizations: the continuous isotropic phase gaslike compression model; ^[25] a considering of a dipole– dipole interaction in scope of the perturbation theory; ^[24] the mean isotropic potential approximation.^{[10, 26, 36]} An external magnetic field suppresses the rotational Brownian motion and aligns nanoparticles magnetic moments, which leads to a mean attraction force increase.^[36] Hence, an external magnetic field stimulates the condensation phase transition^[10] leading to the ascending binodal curve. In the case of a significant correlation of magnetic moments orientations (non-LJ fluid model as discussed above), this conclusion is incorrect because the mean isotropic potential model conditions have been violated: the significantly anisotropic dipole– dipole interaction strongly impacts an equilibrium structure. Such structures with a closed magnetic flux (coils, rings, ring assemblies, tubes, scrolls, etc.^[15]) already correspond to a minimal potential energy and a suppressed entropic summand. The applying of an external magnetic field can only increase the potential energy: flux-closed magnetic structures (Fig. 5(a)) transform into the set of parallel linear chains (Figs. 5(c), 6(a), and 6(c)) where at least marginal particles have a less “ workfunction” comparing to particles inside the ring or tube structure because they are attached to the single magnetic dipole only. Structures with a closed magnetic flux are bounded by the larger dipole– dipole energy. Such aggregate destructs at a higher temperature.

The present simulation results provide a fine structure^{[14, 15]} of the transition from “ linear chains” to “ dense globes” (Figs. 5 and 6) through the ring assembly structure.^{[14, 15]} Oppositely, the above-mentioned assumptions of the theoretical investigations^{[10, 24, 25]} suppress this fine structure. The simulation method suggested here does not imply idealizations of the theoretical models.

The last problem which requires discussion is a relation of the opposite results to experimental studies. Both types of binodal dependencies match the respective experimental observations. Hence, their FF parameters were obviously different. The discussed contradiction has been shown only for the FF parameters of the present research:^{[30, 31]} a small particle coating rate k_c = 5% by an oleic acid which is a concept similar to Ref. [76]. This value allows a random compact packing Ref. [75] in a polydisperse FF by passing a strong surfactant repulsion. This is a non-stabilized type of an FF (Fig. 1(b)) with a high volume fraction of a dispersed phase: an equilibrium state corresponds to the value φ _V ∼ 30%. Oppositely, a “ classical” stabilized FF(k_c = 50%) corresponds to well-separated particles (Fig. 1(a)). The latter means that a correlation in orientations of magnetic moments is small^[26] due to a larger average distance between particles and a corresponding weaker dipole– dipole interaction. In this case the aggregates formation can be modeled by an LG type of a phase transition in the framework of the simple mean-field theory^[22] or the isotropic potential model.^{[26, 36]} In the case of a stabilized FF, an ascending binodal curve theoretical dependence^{[10, 24, 25]} matches very few experimental reports (the reference in Ref. [24]).

This research focuses on the FF aggregate nucleus only. The phase diagram should be verified and generalized to the case of a bulk phase: a larger number of particles and a more durable period of a stabilization. According to the experiment, ^{[30, 31]} this period should have order of magnitude in a range between seconds and minutes time-scales. Taking into account an extensive nature of the current simulation method, ^[78] its natural further development is a parallel computing capabilities implementation. In our opinion, a most promising method of the parallel computation of the FF molecular dynamics is a Graphics Processing Units-based approach.^[52] The open-source project dedicated to a further evolution of the method has been started.^[78] A comparison of present results with ones based on the Monte Carlo simulation is in need of further investigations.^{[38, 41]}