†Corresponding author. E-mail: huibinwu@bit.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11272050).
The skew-gradient representation of a generalized Birkhoffian system is studied. A condition under which the generalized Birkhoffian system can be considered as a skew-gradient system is obtained. The properties of the skew-gradient system are used to study the properties, especially the stability, of the generalized Birkhoffian system. Some examples are given to illustrate the application of the result.
The authors in Ref. [1] pointed out that an ordinary differential equation can be written in a “ linear-gradient system” when its one or more integrations or Lyapunov function is given. The skew-gradient system is a kind of linear-gradient systems which has important significance, and is different from the gradient system given by Ref. [2]. The former’ s matrix is antisymmetric; while the latter’ s matrix is symmetric, and is an identity matrix. Quispel et al.[3, 4] proved that an autonomous ordinary differential equation has a first integral if and only if it can be written as a skew-gradient system, and presented a general method to rewrite such a system as a skew-gradient system, then from which constructed several new integral-preserving discrete gradient methods. Hong et al.[5] discussed the skew-gradient representation of autonomous stochastic differential equations with a conserved quantity, then from which constructed direct/indirect discrete gradient approaches. The Birkhoffian system is a natural generalization of the Hamiltonian system. Great progress on its dynamical research has been achieved.[6– 14] The generalized Birkhoffian system refers to the Birkhoffian system with added terms.[14] We have studied the gradient representation for the generalized Birkhoffian system.[15] In this paper, we will give a condition under which a generalized Birkhoffian system can be rewritten in a skew-gradient system, and discuss the dynamic behaviors, especially integration and stability of the generalized Birkhoffian system by using the property of the skew-gradient system.
The differential equations of the skew-gradient system have the form[1]

where
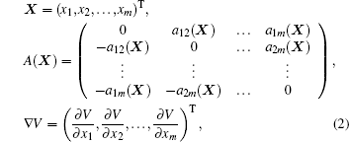
where V is called “ energy” in Ref. [1]. The gradient system given in Ref. [2] has the form
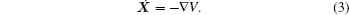
It is clear that equation (1) is different from Eq. (3).
The skew-gradient system has the following important properties. (i) An autonomous ordinary differential equation has a first integral if and only if it can be written as a skew-gradient system. (ii) The energy function V is an integral of the system (1). (iii) If V can be a Lyapunov function, then the solution xi = xi0 (i = 1, 2, … , m) of the system (1) is stable.
The skew-gradient form (1) has many uses. For example, if the system has a first integral V, then its motion stays on the level set Σ C : = {X : V(X) = C}. Preserving this property leads to good nonlinear stability, especially if Σ C is compact.[1] Another example, systems with a Lyapunov function V can be “ weak” or “ strong” . Preserving these properties is important because they are equivalent to the existence of a stable, respectively asymptotically stable, attracting set.[1]
The skew-gradient representation can be used not only to discuss the integration and stability, but also to construct the integral-preserving discrete gradient approaches for the system. In addition, Hamiltonian systems, generalized Hamiltonian systems, and autonomous Birkhoffian systems are skew-gradient systems. Naturally, the results and methods on the skew-gradient system can be applied to these systems.
The generalized Birkhoffian system refers to the Birkhoffian system with added terms. Great progress has been made on its dynamical research.[16]
In general, a generalized Birkhoffian system cannot be rewritten in a skew-gradient system. In the following, we give a condition under which a generalized Birkhoffian system can become a skew-gradient system. In such a case, one can easily discuss the integration and stability or construct integral-preserving discrete gradient methods for the system by using the results of the skew-gradient system.
The nonsingular generalized Birkhoffian equations have the form[14]

where and in the following, the same indices in a term indicate to take the sum with it. In Eqs. (4), B = B(t, a) is the Birkhoffian, Rμ = Rμ (t, a) are Birkhoff’ s functions, and Λ μ = Λ μ (t, a) are the added terms, and

is called Birkhoff’ s tensor, satisfying

For Eqs. (4), if

then we have

In general, equations (8) still cannot become a skew-gradient system. If there is a function V = V(a), satisfying
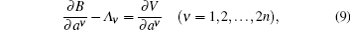
then equations (8) become

Obviously, it is a skew-gradient system. So, under conditions (7) and (9), the generalized Birkhoffian system (1) becomes the skew-gradient system (10).
Taking the derivative of V with respect to time according to Eqs. (10), we have
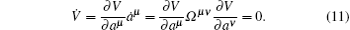
So, V is an integral of system (10). If V can further become a Lyapunov function, then one can discuss the stability of generalized Birkhoffian system (1) by using the property of the skew-gradient system.
For a Birkhoffian system, there are Λ μ = 0 (μ = 1, 2, … , 2n), then an autonomous Birkhoffian system is a skew-gradient system, whose Birkhoffian is an integral. Similarly, if B can further become a Lyapunov function, then one can discuss the stability of the Birkhoffian system.
Example 1 A generalized Birkhoffian system of order 4 is

Try to rewrite it in a skew-gradient system, and discuss the stability of zero solution.
Clearly, condition (7) is satisfied. Condition (9) gives
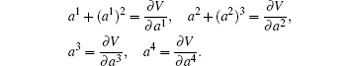
From which one can take
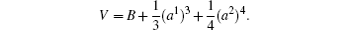
Then equations (10) give
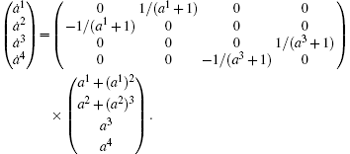
Take function V as a Lyapunov function, which is positive-definite in the neighborhood of a1 = a2 = a3 = a4 = 0. Taking V̇ according to the above equation obtains
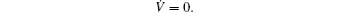
According to the Lyapunov theorem, zero solution a1 = a2 = a3 = a4 = 0 is stable.
Example 2 The Hojman– Urrutia equation has a Birkhoffian representation[6]

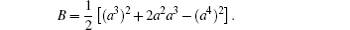
Try to rewrite it in a skew-gradient system.
Equations (10) give
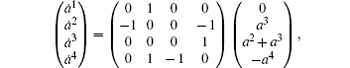
Clearly, it is a skew-gradient system, and function B is an integral of the system. But B cannot become a Lyapunov function.
Generally speaking, a generalized Birkhoffian system is not a skew-gradient system. In this paper, we obtained a condition under which the generalized Birkhoffian system can become a skew-gradient system, namely expressions (7) and (9). When a generalized Birkhoffian system is rewritten in a skew-gradient system, its dynamic behaviors can be discussed by using the properties of the skew-gradient system. Especially, if function V can become a Lyapunov function, then one can discuss the stability of the system.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|


