†Corresponding author. E-mail: yuanjie@nju.edu.cn
‡Corresponding author. E-mail: pcarson@umich.edu
*Project supported in part by DoD/BCRP Idea Award, BC095397P1, the National Natural Science Foundation of China (Grant No. 61201425), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20131280), the Priority Academic Program Development of Jiangsu Provincial Higher Education Institutions, China, and the National Institutes of Health (NIH) of United States (Grant Nos. R01AR060350, R01CA91713, and R01AR055179).
Hyperthermia is a promising method to enhance chemo and radiation therapy of breast cancer. In the process of hyperthermia, temperature monitoring is of great importance to assure the effectiveness of treatment. The transmission speed of ultrasound in biomedical tissue changes with temperature. However, when mapping the speed of sound directly to temperature in each pixel as desired for using all speeds of ultrasound data, temperature bipolar edge enhancement artifacts occur near the boundary of two tissues with different speeds of ultrasound. After the analysis of the reasons for causing these artifacts, an optimized method is introduced to rebuild the temperature field image by using the continuity constraint as the judgment criterion. The significant smoothness of the rebuilding image in the transitional area shows that our proposed method can build a more precise temperature image for controlling the medical thermal treatment.
Surgery, radiation therapy and chemotherapy are widely known as the most common types of cancer treatment and have been studied for a long time. Cancer surgery, [1, 2] an operation to repair or remove part of the body to diagnose or treat cancer, remains the foundation of cancer treatment. Radiation therapy and chemotherapy are methods of killing cancer cells respectively by high-energy radiation and drugs. Many studies[3– 6] have proved the significant effects of these two methods.
With the development of electromagnetic[7] and ultrasonic deep heating, hyperthermia becomes an emerging method for breast tumor treatment. Plenty of researches have proved that the combination of hyperthermia and other methods, especially radiotherapy and chemotherapy, often contributes to better treatment results.[8– 11]
In the process of hyperthermia, temperature monitoring is very important to assure safe treatment.[12] Target temperature ranges are typically quite tight, [13] e.g., 42 ° C or 43 ° C ± 1 ° C, to achieve the highest therapeutic enhancement. Insufficient temperature control not only reduces the effectiveness of hyperthermia but also can cause pain and damage.[14] Temperature measurement methods can be classified as invasive ones and noninvasive ones. Invasive temperature measurement methods are those that heat-sensitive sensors are embedded into tissues. They offer many advantages, such as accurate results, easy operations, and low cost. However, sparse spatial sampling provides temperature information of limited spots instead of the whole tissue[15] and there is some pain and the risk of infection. Non-invasive methods can avoid these problems by not disrupting the skin and other organs. Commonly employed or studied non-invasive measurement methods employ magnetic resonance (MR), [16] microwave, [17, 18] and ultrasound[19, 20] techniques. Three-dimensional (3D) mapping of temperature with the MR method based on the relaxation time, the diffusion coefficient, [21] or proton resonance frequency (PRF)[22] of tissue water has been well described previously. However, these methods only consider the relative temperature changes by comparing a reference image with images acquired under identical experimental conditions. An alternative approach to the calculation of absolute temperature is MR spectroscopic imaging by measuring the water resonance shift.[23, 24] Recently, a real-time MR temperature monitoring method based on the relaxation time of tissue is proposed[25] by demonstrating the capability of real-time simultaneous temperature mapping in aqueous tissue and fat during HIFU ablation. However, the entire process of MR is quite expensive for a cycle of multiple treatments. Techniques based on microwaves to measure temperature can be easily affected by the environment and can only penetrate a limited depth.[26] Ultrasound is a non-ionizing, convenient and inexpensive modality with relatively simple signal processing requirements, which makes it an attractive method to be used for temperature monitoring. Methods of using ultrasound as a temperature measurement include those that measure echo-shift changes in tissue thermal expansion and the speed of sound, [27, 28] those that measure the acoustic attenuation coefficient, [29, 30] and those that exploit the change in backscattered energy (CBE)[31] from tissue in homogeneities. However, the prior knowledge of the speed of sound (SOS) and thermal expansion coefficient are necessary if the echo-shift method is employed.[32]
The structure of heat dissipating a blood vessel[33, 34] in a breast tumor is rather complex, making high resolution temperature imaging critical for uniform thermal therapy or treatment enhancement. Local changes in the speed of sound, [35, 36] attenuation of ultrasound, [37] and thermal conductivity[38] are caused by changes in temperature. Since the thermal coefficient of the speed of ultrasound varies with tissue, the speed of ultrasound in tissue can be used to calculate the temperature field. Temperature distribution in biomedical tissue should meet the following equation:
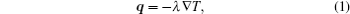
where q is the thermal density, T is the temperature, and λ is the thermal conductivity.
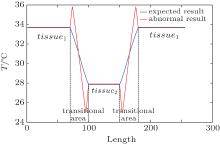
According to Eq. (1), temperature should change monotonically and smoothly. However, when we directly map the value of the speed of sound to obtain the temperature, a bipolar edge enhancement artifact will occur around the boundary of two different tissues. Unlike the ripple artifact, which is often observed around the heated region in the temperature estimations caused by the thermal– acoustic lens effect, [39, 40] the bipolar edge enhancement artifact results from the abrupt change in thermal coefficient of the speed of sound and the finite resolution of the imaging system.
In this paper, we analyze the causes of these artifacts and propose an optimization method to rebuild a correct temperature field image. The rest of this paper is organized as follows. In Section 2, both the direct method and the proposed method of optimally rebuilding the temperature image are presented. In Section 3, the experimental analysis and the quantitative analysis are given for subjective evaluation. Finally, some conclusions and a discussion are given in Section 4.
Usually, the temperature, T, of an object can be described as a function of spatial coordinates x, y, z, and time t as follows:

Since the variation of temperature is a gradual process, we can neglect the time parameter to simplify the partial differential equation of heat conduction for temperature fields into

where ϕ and λ respectively represent the heat generated by the heat source per unit volume per unit time and the thermal conductivity.
2.2.1. Traditional method
By threshold segmentation of the speed of ultrasound image, tissue and its transitional area are separated by the following rule:
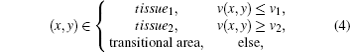
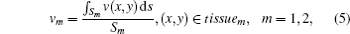
where v(x, y) is the speed of ultrasound at (x, y), v1 and v2 are average ultrasound transmission speeds in tissue1 and tissue2 respectively, Sm (m = 1, 2) are the areas of tissue1 and tissue2 and we suppose v1 < v2.
With the profiles between temperature and speed of ultrasound in tissue1 and tissue2, f1(v) and f2(v), temperatures in tissue1 and tissue2 can be acquired through

The SOS image mixes the speeds of sound of the two tissues at their boundaries due to the finite resolution of the imaging system, given by the system’ s line spread function (LSF), that is,

as the speed of sound in mixtures of homogeneous tissues follows a simple linear mixture model. Equation (7) gives a linear combination of the two different speeds at a sharp vertical boundary with a rectangular LSF. Thus, the measured speed v′ (x) in the transitional area would be
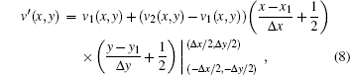
where Δ x = x2 − x1, Δ y = y2 − y1, and (xm, ym) (m = 1, 2) are the points in the boundary of the transitional area and tissuem.
The temperature at a sharp vertical boundary ideally would be given by a similar equation
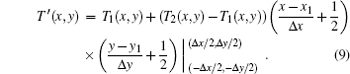
We use the data of the speed of sound in the transitional area with a pixel and conduct the pixel calculation from the speed of sound. The temperature in the mixing area is expressed as

This provides distracting edge enhancement when the transitional area is not accurately segmented by Eq. (4). To illustrate this, suppose that a homogeneous tissue with low temperature is surrounded by a high temperature tissue. When tissues and their transitional areas are well distinguished and equations (6) and (9) are correctly applied, the temperature curve for the model is represented by the blue line in Fig. 1. However, if the boundary between two tissues is an unknown mixture of the two, equation (10) must be employed and even a sharp boundary will have the edge artifacts of the red line when the transitional area is segmented into tissues.
2.2.2. Proposed method with optimization
To allow for thin layers of mixed tissue and using Eq. (10), or one with a different LSF, continuity of temperature distribution is used as a constraint to rebuild the temperature image. After rough segmentation using Eq. (4), the boundary of the transitional area is determined by the following equation:
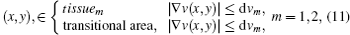
where dvm (m = 1, 2) is the average of the gradient of the speed of ultrasound in the identified tissue1 or tissue2:
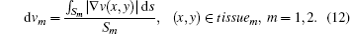
The transitional area is denoted as D, and its boundary as L. Generally, we assume that the whole transitional area is segmented into two parts as Dm (m = 1, 2) by the boundary. Then thermal conductivity λ in each part is a constant. In addition, there is no inner heat source in each transitional area. Thus, equation (3) in each Dm is simplified into
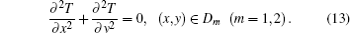
Since the two transitional parts share the boundary, we can obtain the heat conduction equation of the whole transitional area, which is expressed as
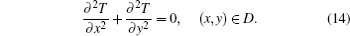
Temperature at L as the boundary condition is calculated by Eqs. (11) and (12) and Eqs. (5) and (6) as follows:
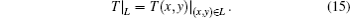
The finite element method[41] is a numerical technique for finding approximate solutions to boundary value problems for partial differential equations. We divide the whole area of interest into similar parts called finite elements and use this method from the calculus of variations to solve the problem. In order to solve Eq. (14) with the boundary condition described in Eq. (15), the transitional area D is divided into m non-overlapped triangles e1, e2, … , em. For all m triangles, there are n non-overlapped vertices d1, d2, … , dm.
For triangle ei (i = 1, 2, … , m), coordinates of its three vertices are denoted as (xi1, yi1), (xi2, yi2), and (xi3, yi3). Equation (15) is used to calculate the coefficient matrix Kei:
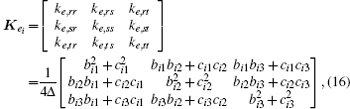
where r, s, and t are the index numbers of the three vertices of triangle ei, and

The n × n matrix K is built by elements kpg from Kei:

Temperature of all vertices is acquired by solving:
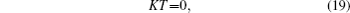
where T = (T1, T2, … , Tn)′ is the vector of the temperature of all vertices. The temperature of vertices on boundary L is given by Eq. (15) as a known boundary condition.
2.2.3. Reconstruction quality evaluation
While rebuilding the temperature field image based on Eq. (14), we take the absolute difference between the temperature of one pixel and the mean temperature of its adjacent four pixels as a criterion to evaluate the smoothness of the rebuilding image, which is expressed as
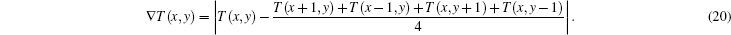
Bipolar edge enhancement artifacts are the abnormal results around the boundary. Mean variation of temperature of adjacent pixels in the transitional area, which is defined in Eq. (21), is calculated as a criterion to evaluate the image quality of the reconstructed temperature field, and is given as
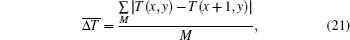
where M is the total number of pixels in the transitional area.
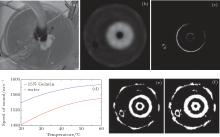
In our experiment, we use a gelatin cylinder with a central flow type to mimic the presence of benign and cancerous masses embedded in glandular tissue as a representative x-ray CT scan of the breast phantom shown in the literature.[42] 15% gelatin and cool water in the tube are respectively used to mimic tumor and fat. To record the transmitted and reflected ultrasound energy, a clinical ultrasound ring array scanner for breast cancer diagnosis, termed computed ultrasound risk evaluation (CURE), has been designed and built at the Karmanos Cancer Institute (KCI), Detroit, MI, USA.[43, 44] During scanning, all transducer elements sequentially emit a fan beam of ultrasound signals toward the opposite side of the ring. The scattered (transmission) and backscattered (reflection) ultrasound signals are subsequently recorded by all elements. Data of all wave fields (including both transmission and reflection) are then used to reconstruct the images of acoustic properties.[42]
Reflection mode and speed of sound images (e.g., Figs. 2(c) and 2(b) respectively) of a gelatin cylinder with a central flow tube (Fig. 2(a)), immersed in water are obtained with a prototype SoftVue® breast imaging system (Delphinus Medical Technologies, Inc., Plymouth, MI, USA). The different sections of the image are segmented from reflection images.
Figure 2(e) shows the original segmented transitional area obtained using Eqs. (4)– (6) and Eq. (10). After applying our proposed method (using Eqs. (11) and (12)), the optimized transitional area is segmented as shown in Fig. 2(f). It is the inaccurate traditional segmentation that is responsible for the nonphysical bipolar edge enhancement, according to our previous analysis. By comparison, it is obvious that the transitional area is optimized with our proposed method.
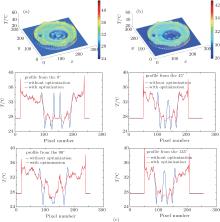
Curves of sound speeds of water and 15% gelatin were interpolated in Refs. [45] and [46], respectively, to make the temperature image and profiles. Figure 3(a) shows the un-optimized three-dimensional (3D) temperature image of the whole gelatin, water and their boundary, obtained by using the traditional direct mapping method. The optimized 3D temperature image of the whole area is shown in Fig. 3(b), calculated by Comsol® Multi-Physics 3.5a with 25 repeated simulations through the finite element method. Figure 3(c) displays the comparison of temperature profile between with and without optimization.
From the 3D temperature image calculated directly by the speed of sound image and a profile of it, we can see that in the transitional area between gelatin and water there are nonphysical bipolar edge enhancement artifacts and the temperature changes sharply. Comparing Fig. 3(a) with Fig. 3(b) and also comparing the blue temperature profile with the red one in Fig. 3(c), after optimization, the edge enhancement artifacts are effectively alleviated and the temperature in the transitional area is much smoother.
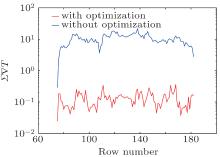
Absolute differences of temperature ∇ T (x, y) from the transitional area with and without optimization in all rebuilt temperature images rows are shown in Fig. 4. The value of ∇ T (x, y) without optimization is much larger than that with optimization, which proves that our proposed method can rebuild a better temperature image which fits Eq. (12) very well. Mean variation of temperature
The structures of breast tissues and in particular breast cancers are rather complex, producing quite non-uninform heating patterns in microwave and ultrasound hyperthermia adjunctive to repeated chemo and radiation therapy sessions. This makes low cost, high speed, high fidelity temperature imaging essential for routine achievement of the benefits of hyperthermia in a cost efficient health care system. The strong bipolar edge enhancement artifacts in the temperature imaging derived from pixel by pixel mapping from the speed of sound will make this task much more difficult. The smoothing achieved with our proposed optimization method is helpful and adaptive. Experimental results show that after optimizing, bipolar edge enhancement artifacts are effectively reduced and the temperature in the transitional area is much smoother. Temperature imaging with transmission tomography for localized feedback of hyperthermia seems quite feasible where stable ultrasound transmission imaging can be achieved.
We thank N. Duric of the Karmanos Cancer Institute, and M. L. Scarpelli of the University of Michigan for contributions to conceptualization and experiments, respectively.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|