As an important type of classic waves, the water surface wave (WSW) has received great attention because rich energy is stored in the WSW of oceans, which is considered as one kind of clean renewable energy to defuse the incoming energy crisis.^{[1– 3]} Its energy density is much larger than that of wind power and solar power, while it is almost immune to weather.^[4] In the past few years, many researches have already been made to study the interactions between WSW and engineering structures such as rippled bottom, ^{[5– 7]} floating disk arrays, ^[8] Helmholtz arrays, ^[9] etc. As a result, many interesting phenomena such as water-wave shifter, negative gravity and complete band gaps have been realized in the modulation of WSW. However, less attention has been paid to wavefront modulation of WSW with a metasurface, which is definitely important for reducing the size of facilities and can greatly extend ways to take advantage of water wave energy or protect the seashore.

Inspired by progress in optical crystals and acoustic crystals, gradient-index (GRIN) media are also applied to the modulation of WSW. For example, it has been demonstrated that a GRIN array made of columns periodically pierced into water can focus WSW.^[10] However, to steer the wave propagation, it requires that the lattice constant of the periodic structure is comparable to the wavelength and at least several lattices are required. It is quite impractical because the wavelength of offshore WSW is often very large. Thus, steering the WSW is difficult to carry out by Bragg scattering in reality. On the other hand, the so-called metasurfaces have drawn significant attention in the optics and acoustics community recently.^{[11– 15]} As a two-dimensional (2D) equivalent of the metamaterial, the metasurface has demonstrated an unusual manipulation of wavefronts with planar profile and sub-wavelength thickness, where the reflection or refraction waves are redirected and follow the so-called generalized Snell’ s law. The newly proposed coiling-up-space metasurfaces show the incomparable advantages that the size is much smaller than the working wavelength.^[16] Many phenomena like sub-wavelength focusing, ^{[17, 18]} acoustic rainbow trapping, ^[19] and negative refraction^[20] have already been realized in acoustic waves by using coiling-up-space metamaterials. The metamaterial with coiling up space is characterized by the zigzag path in the inner structure. Its inner path is much longer than its width so it functions with a large phase delay, providing a feasible way to steer WSW with a metasurface on a sub-wavelength scale.^[21]

In this paper, we investigate the wavefront modulation of WSW by using the GRIN metasurface. A GRIN metasurface is fabricated with an array of coiling-up-space units. The units are designed with special geometrical parameters and there is a phase difference of π /5 between adjacent units. The phase shifts of all units are presented, and appropriate parameters are chosen. As a result, the total width of the designed metasurface is only 0.05  m, which is 1/5.2 of the corresponding working wavelength (0.26  m). By taking the phase gradient into consideration, the generalized Snell’ s law indicates that negative refraction and ‘ driven’ surface mode exist with different incident angles, which has been demonstrated in its electromagnetic counterparts.^[22] We further demonstrate that the WSW could be guided out with a symmetrically-corrugated channel.^{[23, 24]} Our work shows a possibility of improving the power generation efficiency of WSW and protecting the seashore.

In order to describe the vibration mode of WSW, the WSW equation should be solved. In our study, the water is assumed to be linear. First, we set x– y in the horizontal plane and z as the vertical axis. Here, the bottom of the water is set at z = − h₀ and the free surface at z = 0. Ignoring the surface tension effect and viscous effect, and assuming that water is incompressible and irrotational, the governing equation for propagation of WSW can be expressed by the 2D Helmholtz equation as follows:^{[25, 26]}

where ω is the angular frequency of WSW, g is the gravitational acceleration, u = tanh(kh₀)/k is called the reduced water depth, and k is the wave number of incident waves. Thus the velocity potential Φ and vertical displacement of the liquid surface η are shown as

Here, λ is the wavelength. Because no flow is allowed to pass through the rigid plates, the boundary condition of the surface between the water channels and the rigid plates is ∂ φ /∂ n₀ = 0, where n₀ represents the direction normal to the plates. In a system with a constant water depth h₀, the dispersion relation of linear WSW satisfies ω ² = gk tanh(kh₀). In the study, when WSW propagates through the curled channels in units, its travel path is multiplied and its phase is greatly delayed, which is demonstrated to be controllable during building a WSW metasurface.

A three-dimensional (3D) view of the coiling-up-space unit for WSW with zigzag paths is shown in Fig.  1(a). The unit with a height of h₁ is pierced in water and the depth of water is h₀. Here, h₁ is larger than h₀ to ensure that the structure is not inundated by water. The thin pedestal lying below is used to support the structure and is negligible. Figure  1(b) shows a top view of the unit. Its length and width are a = 0.05  m and b = 0.051  m, respectively. The thickness of the rigid plate is w and the channel width between adjacent plates is d = (a − 8w)/n ≈ 6.6  mm, where n denotes the number of the curled channels. The inner channels formed by those plates can be adjusted by adding/removing plates. When WSW propagates through the zigzag channels, the total travelling path is multiplied compared with the unit length and then a huge phase delay occurs. Besides, for the WSW passing through the unit, the phase delay can be adjusted easily by carefully selecting the plate length l and channel number n. Here, the vibrating frequency of the WSW is set to be 2.45  Hz, which corresponds to a WSW wavelength of 0.26  m, i.e., just 5.2 times larger than the unit width (0.05  m). In order to choose the appropriate parameters of a coiling-up-space unit, the phase shifts of a unit with different values of plate length l and channel number n are illustrated in Fig.  1(c). It is found that the phase delay increases gradually and continuously as plate length increases. For two units with the same plate length, the one with more channels contributes to a larger phase delay. All the enlarged phase delays can be ascribed to the increased total zigzag path for travelling. In order to design a GRIN metasurface to steer WSW, a gradient phase shift should be achieved in the metasurface. In addition, for all of the chosen units, the composed period should cover a huge phase delay of exactly 2π . It is clearly observed from Fig.  1(c) that the phase delay is highly controllable and wide enough, which is important to build a steering metasurface.

According to Fig.  1(c), ten coiling-up-space units are carefully designed and arranged in a line to form a period as shown in Fig.  2(a). The upper panel in Fig.  2(a) gives out exactly the phase delay and the plate length for each of the desired units. The lower panel in Fig.  2(a) presents the schematic diagram of a period (10 units) as well as the channel number for each unit. By elaborately designing the channel number and plate length, there is a phase difference of π /5 between two adjacent units and the whole phase range (2π ) is covered in a period. Note that for a specified phase delay, several combinations of channel number and plate length may be qualified. By choosing the appropriate combinations, the ten units are designed to have relatively high and approximately the same transmission, which is essential to build a wave shifter. Thus, a metasurface is constructed with an array of such periods in a planar profile and is thin in thickness (about 1/5.2 of the wavelength). According to the generalized Snell’ s law, k₀(sin θ _t − sin θ _i) = ξ when the WSW is incident on the designed metasurface at an incident angle θ _i, where θ _t is the refracted angle, k₀ is the wave number, and ξ is the phase gradient. The phase delay gradient is expressed as Δ φ /L, where Δ φ is the phase range and L is the length of the period. Here, k₀ = 24.2  rad/m, ξ = Δ φ /L = 12.32  rad/m. The calculated relation between incident angle and refracted angle is plotted in Fig.  2(b). The generalized Snell’ s law indicates that the refracted angle θ _t = asin(sin θ _i + Δ φ /L/k₀). Thus the refracted angle is 30.7° under the normal incidence condition. If the incident angle has critical value θ _c1 = asin(− Δ φ /L/k₀) = − 30.7° , the transmitted WSW is normal to the metasurface. As a result, on the basis of Fig.  2(b), it can be easily found that a negative refraction occurs when θ _i varies between θ _c1 and 0° as shown by the yellow area in Fig.  2(b). In addition, if the incident angle is bigger than θ _c2 = asin(1− Δ φ /L/k₀) = 29.4° (the cyan area), the transmitted wave turns into a wave in the so called ‘ driven’ surface mode, which is demonstrated in its electromagnetic and acoustic counterparts.^{[27, 28]} The ‘ driven’ surface wave could not propagate along the metasurface and is localized to the incident field region because a ‘ driven’ surface mode is not the eigenmode of the metasurface, but can be guided out with a proper coupling mechanism efficiently.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Schematic view of a coiling-up-space structure with a layer of thin pedestal placed in water. The height h1 is 2.5  m and the water depth h0 is 2  m. (b) Top view of the structure. The length of rigid plate is expressed as l, and n denotes the number of the curled channels. (c) The phase shift of a metamaterial versus plate length l and channel number n.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Phase shift (left) and plate length (right) for the ten chosen metamaterial units (upper panel) and schematic view of one period (10 units) of the designed metasurface and the channel number corresponding to each unit (lower panel). (b) The theoretical refracted angle θ t as a function of the incident angle θ i, calculated by the generalized Snell’ s law.

In order to verify the steering effect of the metasurface, full-wave simulations are performed. As shown in Fig.  3, the metasurface is composed of four periods and thus a total of 40 coiling-up-space units are used. Figures  3(a) and 3(b) present the temporal fields for oblique incidences of θ ₁ (20° ) and θ ₂ (− 20° ) each with a Gaussian beam, which are located in the areas of positive and negative refraction, respectively. Figures  3(c) and 3(d) give the respective amplitude field patterns. Because the incident angle θ ₂ falls in a range of (θ _c1, 0° ), the occasion could be treated as a negative refraction by comparing Fig.  3(b) with Fig.  3(a). To examine the modulating effect more intuitively, the theoretical results calculated from the generalized Snell’ s law are also plotted in the upper parts of figures with white arrows (θ _t ∼ 58.4° in Fig.  3(a) and 9.7° in Fig.  3(b)). It is clearly demonstrated that the WSW metasurface modulates WSW stably and accords well with the theoretical results. Here, it should be noted that the reflections at the input originate from the imperfect impedance matching between metasurface and water.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Temporal fields for WSW with Gaussian envelope propagating through the designed metasurface with incident angles (a) θ 1 = 20° and (b) θ 2 = − 20° , where white arrows show the theoretical propagating directions of the wave front, (c) and (d) the amplitude fields corresponding to panels (a) and (b), respectively.

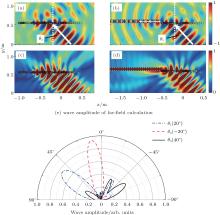
According to generalized Snell’ s law, the transmitted WSW would be totally bent towards the metasurface, and the ‘ driven’ surface mode comes into being if the incident angle is larger than θ _c2 (29.4° ). Compared with a conventional surface mode, the ‘ driven’ surface mode does not require a specific incident angle but could not propagate along the interface.^[28] We further investigate the occasion where the incident angle θ ₃ is 40° (> θ _c2 ∼ 29.4° ). Figure  4 shows (a) temporal field and (c) amplitude field for WSW propagating through the metasurface with incident angle θ _i = 40° . It is found that the WSW could not propagate along the interface under such a circumstance. In order to convert such a ‘ driven’ surface mode into the propagating surface mode, a bottom-mounted and symmetrically-corrugated channel with periodic slots cut on both sides is pierced into water and connected with the metasurface. The slots have a period of 0.051  m, which is equal to the width of the metasurface unit in order to convert the driven surface mode into propagating mode with minimum loss.^[27] The channel widths are 0.07  m and 0.04  m in adjacent areas, respectively, which are all much smaller than half the wavelength of incident WSW. Thus, higher modes should be evanescent and only the main mode can propagate.^{[23, 24]} In Figs.  4(b) and 4(d), the constrained WSW is successfully coupled by the channel and propagates, which is useful in capturing the energy of WSW to generate electricity. Furthermore, in order to verify the wave field results quantitatively, the far-field distributions of transmitted WSW with 20° , − 20° , and 40° incidence are presented in Fig.  4(e). For comparison, it is normalized with the maximum amplitude of the incident WSW with a Gaussian envelope. The plots of 20° (− 20° ) incidence show a clear main lobe along 58.4° (9.7° ), indicating that the WSW is efficiently shifted by positive (negative) refraction. However, in the case of incidence with 40° , little energy can be radiated. Note that the small side lobes come from the imperfect parameters of manufacture and can be further optimized by making the width between adjacent plates changeable or designing a variable plate length for each plate of a single coiling-up-space unit.^[29]

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. (a) Temporal and (c) amplitude fields for WSW propagating through the metasurface with incident angle θ 3 = 40° . (b) Temporal and (d) amplitude fields for WSW propagating through the metasurface linked with symmetrically-corrugated channel. The corrugated sidewalls have a period of 0.051  m. (e) The calculated far-field amplitude distributions of transmitted WSW with incident angles of 20° (dash dotted line), − 20° (dashed line), and 40° (solid line), respectively.

In conclusion, we have come up with a planar metasurface composed of an array of metamaterial units built with a coiling up space. The metasurface works on a deep sub-wavelength scale and phase gradient is achieved by elaborately designing the geometric parameters. Under certain circumstances the amazing negative refraction and ‘ driven’ surface mode are realized. The metasurface succeeds in modulating the wavefront of WSW and the results accord well with those from the generalized Snell’ s law. This work shows potential applications in energy extraction and coastal protection.