†Corresponding author. E-mail: zmzhang@scnu.edu.cn
*Project supported by the Major Research Plan of the National Natural Science Foundation of China (Grant No. 91121023), the National Natural Science Foundation of China (Grant Nos. 61378012 and 60978009), the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20124407110009), the National Basic Research Program of China (Grant Nos. 2011CBA00200 and 2013CB921804), and the Program for Changjiang Scholar and Innovative Research Team in Universities, China (Grant No. IRT1243).
We theoretically investigate the entanglement properties in a hybrid system consisting of an optical cavity–array coupled to a mechanical resonator. We show that the steady state of the system presents bipartite continuous variable entanglement in an experimentally accessible parameter regime. The effects of the cavity–cavity coupling strength on the bipartite entanglements in the field–mirror subsystem and in the field–field subsystem are studied. We further find that the entanglement between the adjacent cavity and the movable mirror can be entirely transferred to the distant cavity and mirror by properly choosing the cavity detunings and the coupling strength in the two-cavity case. Surprisingly, such a remote macroscopic entanglement tends to be stable in the large coupling regime and persists for environment temperatures at above 25 K in the three-cavity case. Such optomechanical systems can be used for the realization of continuous variable quantum information interfaces and networks.
Entanglement, an important trait in quantum mechanics, has become a key resource for many quantum processes.[1] Entanglement can be experimentally prepared and manipulated in microscopic systems, such as photons, ions, and atoms.[2] However, it is not yet completely clear to what extent quantum mechanics applies to macroscopic objects. Quantum phenomena such as entanglement generally do not appear in the macroscopic world due to environment-induced decoherence, which is thought to be the main cause that reduces any quantum superposition to a classical statistical mixture.[3] Nonetheless, with the spectacular level of experimental advancements, it has been possible to see macroscopic quantum superpositions.[4]
Cavity optomechanical systems have become important candidates for exploring what extent of quantum entanglement we can obtain at the macroscopic level[5– 13] due to the rapid progress of nanotechnology. The simplest scheme capable of generating stationary optomechanical entanglement is studied in a typical optomechanical setup, [14] where the entanglement between the cavity and the movable mirror is remarkable for its simplicity and robustness against temperature. In recent years, various schemes to generate bipartite entanglements have been proposed, such as the field– mirror entanglement, [15– 20] and the mirror– mirror entanglement.[21– 24] These studies show that entanglement can be influenced by the factors of the cavity optomechanical system such as the intensity of incident laser and the cavity– pump field detuning. In fact, entangled optomechanical systems have potential profitable applications in realizing quantum communication networks, in which the mechanical modes play the vital role of local nodes where quantum information can be stored and retrieved, and optical modes carry the information between the nodes. This allows the implementation of continuous variable (CV) quantum teleportation, [25, 26] quantum telecloning, [27] and entanglement swapping.[28]
Recently, much attention has been focused on the coupled cavity– array (CCA), [29, 30] for which some potential technologies have been demonstrated in experiment.[31, 32] The system is thought to be suitable for building a large-scale architecture for quantum information processing.[33] These observations remind us of the necessity to explore the entanglement properties in a CCA with one oscillating end-mirror. Different from the conventional CCA with a fixed end-mirror, the end mirror in our system is modelled as a quantum-mechanical harmonic oscillator. Due to the long decoherence of the mechanical harmonic oscillator, the information storage time of the mechanical harmonic oscillator is longer than the field. Hence, it is helpful to the study of information transfer and information storage in the quantum information processing. In this paper, we investigate the stationary bipartite CV entanglement in this coupled system quantified by the logarithmic negativity. We also show how the stationary entanglement between the adjacent optical cavity field and the mirror can be transferred to the remote optical cavity field and the mirror by selecting appropriately the cavity– pump field detunings and the coupling strength between coupled cavities. However, the field– field entanglement is small at the same time. Moreover, such distant entanglement between two non-interacting subsystems is robust against temperature above 25 K.
The remainder of this paper is organized as follows. In Section 2 we present the model under study and the analytical expressions of the optomechanical system, derive the quantum Langevin equations and the steady state of the system. In Section 3, we quantify the entanglement properties of the system by using the logarithmic negativity. Finally we draw our conclusions in Section 4.
As schematically shown in Fig. 1, the system consists of n coupled cavities (1, 2, 3, … , N) with coupling constant J. Cavity 1 is driven by a pump field, and cavity N consists of an oscillating mirror at one end, modelled as a quantum-mechanical harmonic oscillator. In the rotating frame with frequency ω 0 of the pump field, the Hamilton is given by

where 


Using the Heisenberg equations of motion, and taking into account the corresponding damping and noise terms, we can get the quantum Langevin equations for the operators of the mechanical and optical modes


in which we have assumed that all cavity– fields have the same decay rate κ . The mechanical oscillator is connected to a thermal bath at a damping rate γ m with a mean thermal excitation number n̄ = 1/(eℏ ω m/kBT − 1), where kB is the Boltzmann constant and T is the temperature of the mechanical bath. The mechanical mode is also affected by a random Brownian force ξ with correlation function 〈 ξ (t)ξ (t′ )〉 ≃ γ m(2n̄ + 1)δ (t − t′ ). Furthermore, 
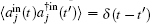
The steady-state mean values of the system can be obtained by setting the time derivatives to zero:

where 
We can divide each Heisenberg operator as a steady-state value plus an additional fluctuation operator with zero-mean value, i.e., q = qs + δ q, p = ps + δ p, aj = ajs + δ aj (j = 1, 2), and get the linearized Langevin equations by neglecting some small quantities

where G1 = ga2s is the effective coupling strength.
In a similar way, we can get the steady-state mean values in the case of three cavities

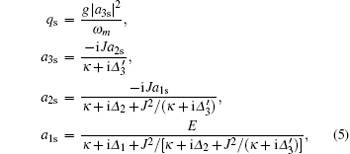
and the linearized Langevin equations
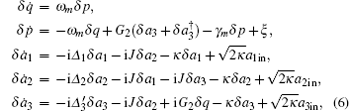
where 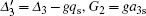
In this section we mainly study the entanglement between any two subsystems in this system. Here we define the cavity field quadratures

and the corresponding Hermitian input noise operators

Then equations (4) and (6) can be rewritten as a matrix form
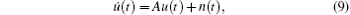
in which the transposes of the column vector u(t), n(t) can be expressed as
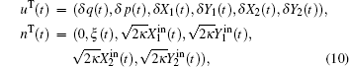
in the case of two coupled cavities, and

in the case of three coupled cavities. The matrix A in these two cases can be given by
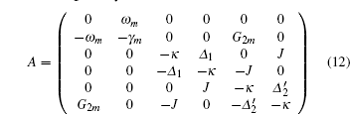
and
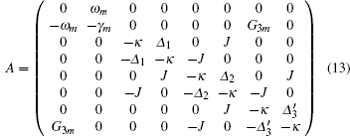
respectively, where 


where M(t) = exp(At). The system is stable only if the real parts of all the eigenvalues of matrix A are negative, which can be derived by applying the Routh– Hurwitz criterion.[34] We will choose the parameters so that the system is subsequently in a steady state. We define Vij = 〈 ui(∞ )uj(∞ ) + uj(∞ )ui(∞ )〉 /2, which is a 6 × 6 (8 × 8) correlation matrix (CM). Here
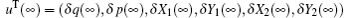
or

is the vector of continuous variables fluctuations operators at the steady state. When the system is stable (t → ∞ ), we get

where Φ kl(t − t′ ) = (〈 nk(t)nl(t′ ) + nl(t′ )nk(t)〉 )/2 is the steady-state noise CM. When the stability conditions are satisfied, the steady-state CM satisfies a Lyapunov equation
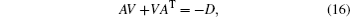
where D = diag[0, γ m(2n̄ + 1), κ , κ , κ , κ ] (N = 2) (or D = diag[0, γ m(2n̄ + 1), κ , κ , κ , κ , κ , κ ] (N = 3)). We can straightforwardly have the solution of the CM with Eq. (16). However, the explicit expression is too complicated and will not be reported here.
Then we will examine the entanglement properties of the steady state of the tripartite system under consideration. For this purpose, we consider the entanglement of the possible bipartite subsystems that can be obtained by tracing over the remaining degrees of the freedom. This bipartite entanglement will be quantified by using the logarithmic negativity

where
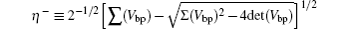
is the lowest symplectic eigenvalue of the partial transpose of the 4 × 4 CM, Vbp, associated with the selected bipartition, obtained by neglecting the rows and columns of the uninteresting mode,
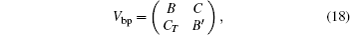
and Σ (Vbp) ≡ detB + detB′ − 2detC.
Firstly, we will study the optomechanical entanglement in two coupled cavities case. In order to investigate the behavior of CV entanglement between the elements of the tripartite system in this case, we will denote the logarithmic negativity for the mirror– cavity 1, mirror– cavity 2, and cavity 1– cavity 2 entanglements as 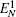
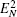

| Table 1. The parameters used in our numerical calculations, taken from the experiments in Ref. [35]. |
For the sake of simplicity, we assume 

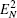



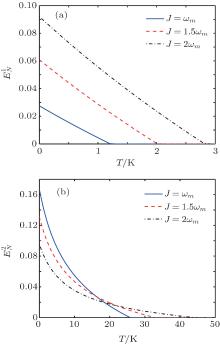
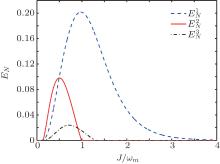 | Fig. 3. Plot of the logarithmic negativity    |
For clearly presenting the effect of cavity– cavity coupling strength on the optomechanical entanglement, we plot 


It is also important to understand the behavior of entanglement with respect to the temperature T. We finally discuss the robustness of optomechanical entanglement (

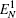
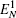
Then we will investigate the optomechanical entanglement properties in the case of three coupled cavities. In this case, we mainly discuss the entanglement between the three cavities and mirror since the entanglement between three cavities is too small. We will denote the logarithmic negativities for the mirror– field 1, mirror– field 2, and mirror– field 3 bimodal partitions as 

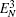
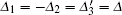

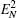
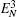

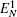

In Fig. 6, we also plot the logarithmic negativity 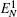
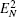



 | Fig. 6. Plot of the logarithmic negativity 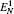    |
The robustness of the optomechanical entanglement 


In conclusion, we have studied the properties of optomechanical entanglement in a coupled cavity– array with a movable mirror through the logarithmic negativity. We mainly considered two cases of a different number of coupled cavity (two and three cavities). Our results show that the entanglement of the adjacent cavity and mirror can be entirely transferred to the remote cavity and mirror due to cavity– cavity coupling in the case of two coupled cavities. Such an optomechanical entanglement between the distant cavity mode and the mechanical mode of the mirror is sensitive to cavity– cavity coupling strength and cavity– pump detunings. The stationary distant entanglement can be achievable through strong cavity– cavity coupling when 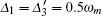
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|