†Corresponding author. E-mail: ygpeng@sdu.edu.cn
‡Corresponding author. E-mail: yzheng@sdu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grand Nos. 91021009, 21073110, and 11374191), the Natural Science Foundation of Shandong Province, China (Grant No. ZR2013AQ020), the Postdoctoral Science Foundation of China (Grant No. 2013M531584), the Doctoral Program of Higher Education of China (Grant Nos. 20130131110005 and 20130131120006), and the Taishan Scholarship Project of Shandong Province, China.
We study the two coupling two-level single molecules driven by an external field as a photon pair source. The probability of emitting two photons, P2, is employed to describe the photon pair source quality in a short time, and the correlation coefficient R AB is employed to describe the photon pair source quality in a long time limit. The results demonstrate that the coupling single quantum emitters can be considered as a stable photon pair source.
The deterministic single photon source and photon pair source are important for quantum information, quantum computing, and quantum communications.[1– 5] In quantum communications, most of the communication protocols are based on entangled photon pairs.[6– 9] Generally, there are two ways to generate entangled photon pairs: one is to use parametric down conversion in nonlinear optical media, and the emission photons satisfy the Poissonian statistics; [10] the other way is to use the radiative recombination of the bi-exciton state in single quantum dots.[10] The last method cannot avoid the effect of the single photon process.
We suggest that two single quantum emitters are coupled as a stable photon pairs source. Because the coupled two single quantum emitters show the same energy structure as that of the single quantum dots, and the coupling between the single quantum emitters demonstrates the two-photon resonance peak at 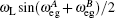

In this paper, we consider the two coupled single quantum emitters as a photon pair source. The coupling of the two single quantum emitters provides a way to excite the two single quantum emitters to their excited states (the bi-exciton states) by a single external field. The external field excites the emitter A into its excited state, then the emitters A and B exchange their status, and the external field then excites the emitter A into its excited state again, which combines into a bi-exciton state. When the external field satisfies 
The rest of this paper is organized as follows. In Section 2 the model of the coupled two single quantum emitters is introduced, and the generating function approach is briefly reviewed. In Section 3, we demonstrate the main numerical results, and a short discussion is also presented. Some conclusions are drawn in Section 4.
We consider two separated single quantum emitters A and B, which are coupled through the dipole– dipole interaction. The emitters A and B can be described as a two-level system. The energy states of the emitters A and B are denoted by | gA〉 and | gB〉 (ground states), respectively, | eA〉 and | eB〉 (excited states) respectively. The transition frequencies of emitters A and B are 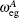

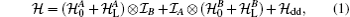
where 
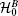


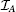
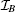
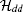
The “ bare” Hamiltonians, in the rotating wave approximation (RWA), can be written as

where 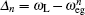
The Hamiltonians of the interaction between emitters and external field in the RWA can be written as

where h.c. represents the Hermitian conjugate, 

The coupling Hamiltonian of the two emitters, the dipole– dipole interaction, can be written as[11, 13, 14]

with
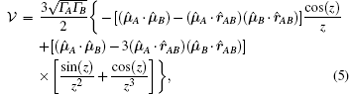
where 



The evolution of the system can be described by the Liouville-von Neumann equation[15, 16]

where 
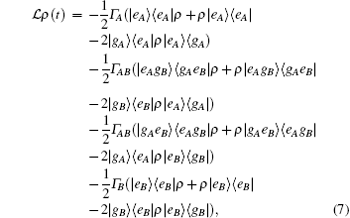
where Γ A and Γ B are the spontaneous emission rates of emitters A and B, Γ AB is the cross damping rate, which can be written as[11, 13, 14]

The spontaneous emission rates Γ n, (n = A, B) read
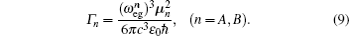
The generating function satisfies

where 


The working generating function is defined as

where | m〉 = | gAgB〉 , | gAeB〉 , | eAgB〉 , and | eAeB〉 .
The moments of emission photons from emitters A and B can be written as

the corresponding Mandel’ s Q parameters can be expressed as

The moments of the total emission photons can also be expressed as
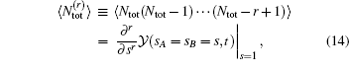
and the corresponding Mandel’ s Q parameter Qtot can be written as
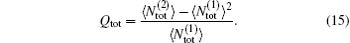
The correlation of the photons, emission from emitters A and B, is[18]

and the correlation coefficent can be written as[19, 20]

where
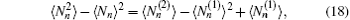
with n = A and B.
The probability of emitting m photons in time interval [0, t] can be written as
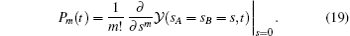
In this section, we consider the single terrylene molecules in a paraterphenyl crystal.[11, 12] The system has been used to demonstrate the high spatial resolution and two-photon resonance, [12] and implemented some quantum gates in the small quantum network.[11] The spontaneous emission rates of molecule A and molecule B are Γ A = Γ B = 50 MHz.[11, 12] The cross damping rate Γ AB = 9 MHz, and the interaction between molecules A and B is 

The probabilities of emitting one, two, and more photons at Δ A = Δ ω /2 are shown in Fig. 4, while the central peak (Δ A = Δ ω /2) is known as the two-photon resonance peak. Figures 1(a)– 1(c) correspond to the Rabi frequencies Ω A = Ω B = 50, 100, and 150 MHz, respectively. The solid lines correspond to the probabilities of emitting one photon [P1(t)], the dashed lines correspond to the probabilities of emitting two photons [P2(t)], and the dash-dotted lines correspond to the probabilities of emitting multi- photons [Pmulti(t)]. From the figures, one could know that the maximum value of the probability of emitting two photons is two times greater than that of the probability of emitting one photon, for all the driving field strengths.
 | Fig. 1. Probabilities of emitting one, two, and more photons versus evolution time t, with the detuning frequency Δ A = Δ ω /2. Panels (a), (b), and (c) correspond to the Rabi frequencies Ω A = Ω B = 50, 100, and 150 MHz, respectively. The other parameters are the same as those in Fig. 1. The solid lines correspond to the probabilities of emitting one photon P1(t), dashed lines correspond to the probabilities of emitting two photons P2(t), and the dash-dotted lines correspond to the probabilities of emitting multi- photon Pmulti(t) = 1 − P0(t) − P1(t) − P2(t). |
The values of correlation coefficent RAB of the photons emitted from molecule A and molecule B are shown in Fig. 2. Figures 2(a)– 2(c) correspond to the weak, medium, and strong driving fields, respectively. The correlation coefficent RAB shows a similar behavior to Mandel’ s Q parameter Qtot. At the left and right resonance peak positions, the correlation coefficient RAB is negative, the negative correlation, of the photons emitted from molecules A and B, means the molecules A and B cannot emit photons at the same time. On the weak driving field condition, the photons emitted from molecule A and molecule B show positive correlation at the peak position (Δ A = Δ ω /2), which means that molecule A emits a photon at time interval [t, t + dt], while molecule B has a big probability to emit a photon at the same time interval [t, t + dt]. The photons emitted from molecule A and molecule B are bunching together, which makes Mandel’ s Q parameter greater than zero. The correlation coefficient RAB first increases and then decreases with the driving field strength inceasing, which means that the strong driving field destroys the correlation of the photons emitted from molecules A and B.
 | Fig. 2. The correlation coefficent RAB versus the detuning frequency Δ A. (a), (b), and (c) correspond to the Rabi frequencies Ω A = Ω B = 50, 100, and 150 MHz, respectively. The other parameters are the same as those in Fig. 3. |
The emission photons 〈 N〉 and Mandel’ s Q parameters versus the detuning frequency 
From Fig. 3, one can know that the total emission photon number 〈 Ntot〉 emitted from molecules A and B is a little smaller than the photon number 〈 NB〉 emitted from molecule B at the left peak, and a little greater than the photon number 〈 NA〉 emitted from molecule A at the right peak, for all the driving field strengths Ω A = Ω B = 50 MHz (weak condition), 100 MHz (medium condition), and 150 MHz (strong condition). The differences between the total emission photons 〈 Ntot〉 and the emission photons 〈 NA〉 and 〈 NB〉 are caused by the coherence of the states | eAgB〉 and | gAeB〉 , and the virtual photons emission and absorption between the states.[21] The dipole– dipole interaction 
In this paper, we consider a system with two coupling two-level single molecules as a photon pair source. The probabilities of emitting one, two-, and multi- photons: P1(t), P2(t), and Pmulti(t), are respectively calculated at Δ A = Δ ω /2 via generating function approach. In a short time region, the probability of emitting two photons is three times greater than the probabilities of emission one and more photons. That means that in a short time, the system is a good two-photon source. In a long time region, the correlation coefficient RAB is introduced to describe the coincidence of the emission photons, and on the weak driving field condition, the correlation coefficient and the Mandel’ s Q parameter Qtot show that the emitted photons are bunching. The system could emit the photon pair train driven by a weak field. As the driving field increases, the correlation between the emission photons is destroyed by the driving field.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|



