†Corresponding author. E-mail: mxjin@jlu.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2013CB922200), the National Natural Science Foundation of China (Grant Nos. 11034003, 11474129, 11274141, and 11304116), the Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20130061110021), and the Graduate Innovation Fund of Jilin University (Grant No. 2015091).
We propose a scheme to coherently control the field-free orientation of NO molecule whose rotational temperature is above 0 K. It is found that the maximum molecular orientation is affected by two factors: one is the sum of the population of M = 0 rotational states and the other is their distribution, however, their distribution plays a much more significant role in molecular orientation than the sum of their population. By adopting a series of linearly polarized pulses resonant with the rotational states, the distribution of M = 0 rotational states is well rearranged. Though the number of pulses used is small, a relatively high orientation degree can be obtained. This scheme provides a promising approach to the achievement of a good orientation effect.
For a linear polar molecule, as the molecular axis is aligned along a particular direction, the alignment process occurs, which has been well investigated and brought into good practical applications. On the other hand, as the molecular axis points along a particular direction, the orientation occurs, which is a more challenging topic. The molecular orientation steered by laser pulses has attracted much attention because of its extensive applications in the control or catalysis of chemical reaction dynamics, [1– 6] detection and quantitative analysis of trace amounts of chemical components[7, 8] and high-order harmonic generation as well as attosecond science, [9– 13] etc.
Various techniques have been applied to the molecular orientation, such as the intense dc field, [14, 15] the two-color laser field, [16– 20] the half-cycle or few-cycle terahertz pulses, [21– 27] and the combination of an intense laser field with a weak dc field.[28– 31] Usually, the molecular orientation degree is limited by the maximally applicable laser intensity before its intrinsic saturation and ionization. What is more, the orientation degree obtained through these techniques is not very high. It is shown in Refs. [32]– [36] that the population of rotational states can be precisely controlled via the coherent control of resonant pulses, and more importantly, the intensity of the laser pulses used in coherent control is weak, which is far below the ionization threshold and the value of intrinsic saturation. For this reason, field-free orientation via resonant pulses is a promising approach. In practice, a good orientation effect has been obtained by this method.[35, 37– 39] However, most of these studies are usually based on the molecules whose rotational temperature is 0 K.[38, 39] As is well known, it is just an ideal case, for it is impossible to obtain molecules of this kind. Consequently, molecular orientation at higher rotational temperature is required. Chi et al. used a series of circularly polarized pulses with the aid of linearly polarized pulses, all of which are resonant with the molecular rotational transitions, to orient the NO molecule at a rotational temperature of 10 K, and quite a high orientation degree was achieved.[37] In addition, in our previous work, a single ground rotational state with high probability has been prepared from an arbitrary superposition state by the PPSQS scheme.[35] However, the pulse number used in these studies is too large, thereby restricting its applications in the experiments.
In this paper, the NO molecule of which the rotational temperature is above 10 K is taken as the computational example. By only adopting several linearly polarized resonant pulses, we attempt to obtain a relative high orientation degree by rearranging the distribution of the M = 0 rotational states.
The initial populations of rotational states |J, M〉 (where J denotes the rotational angular quantum number and M represents the corresponding magnetic quantum number) are given by the Boltzmann distribution at a certain temperature T:
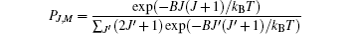
(kB is the Boltzmann constant). The rotational wave-function can be expanded into the unperturbed molecular rotational eigenstates, i.e., the spherical harmonics basis[10, 16]
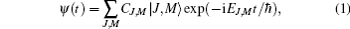
where EJ, M denotes the eigenenergy of the |J, M〉 state, which depends on J and is independent of M, and the population of the rotational state |J, M〉 is determined by PJ, M = |CJ, M|2.
In this paper, the NO molecule is taken as the computational example. Since the amplitude of the external field employed here is moderate, only the permanent dipole moment plays a significant role, therefore, the NO molecule can be modeled as a rigid rotor under this circumstance. In the calculation, we only consider the NO molecule in its 1Σ electronic and ground vibrational state. As a result, the Hamiltonian of NO molecule in the laser field can be defined as

where ω = E0μ 0/B is the dimensionless field– molecule interaction parameter; B and μ 0 are the rotation constant and the permanent dipole moment of the molecule; E0 and f(t) are the peak amplitude and envelope of the external laser field, respectively.
The time-evolution of population parameter CJ, M (t) can be described by substituting Eq. (1) into the time-dependent Schrö dinger equation:

The expectation value of the orientation degree of a linear molecule can be calculated as
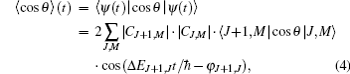
where 〈 J+ 1, M|cos θ |J, M〉 is a transition matrix element, Δ EJ+ 1, J and φ J+ 1, J are the energy difference between the offset phase of two neighboring rotational states, and their expressions are given by
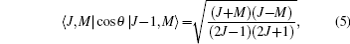
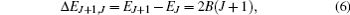

For the NO molecule adopted in this paper, the values of its rotational constant and permanent dipole moment are B = 1.703 cm− 1 and μ 0 = 0.153D, respectively. In the calculation, the dimensionless field– molecule interaction parameter is set as ω = E0μ 0/B= 0.1, and the corresponding electric field strength is E0= 6.63 × 104 V/cm, which is far below the ionization threshold and the value of intrinsic saturation. For convenience, ħ /B (Trot = π ħ /B ≈ 9.79 ps is the molecular rotational period) and B are taken as the units of time and energy throughout this paper.
Figure 1 shows the initial distribution of probability amplitude | CJ, M| of NO molecule at a rotational temperature of 10 K. It can be seen from the figure that the populations of the | 6, M〉 states are so small that they can even be neglected, indicating that as the maximum value of J is set to be 6, it is quite close to the actual case. We can see from Eq. (5) that three factors affect the molecular orientation: probability amplitude | CJ, M| , which remains constant under field-free conditions; offset phase of two neighboring rotational states cos [Δ EJ+ 1, J– φ J+ 1, J], whose value varies between ± 1; the matrix elements 〈 J+ 1, M| cos θ | J, M〉 . It can be seen from Eq. (5) that for the same J, the smaller the value of | M| , the larger the value of 〈 J+ 1, M| cos θ | J, M〉 is. Therefore, the maximum molecular orientation degree is affected by two factors: one is the sum of the population of M = 0 rotational states and the other is their distribution. In general, the larger the sum of the population of M = 0 rotational states, the higher the orientation degree will be, and this can be realized by transferring the population on M ≠ 0 rotational states to the M = 0 rotational states. Chi et al. used a series of circularly and linearly polarized pulses resonant with the molecular rotational transitions to achieve this goal, and by this means, one can prepare a rotational wave-packet populating mainly on a few of the lowest rotational eigenstates whose magnetic quantum numbers are M = 0.[37] High as the orientation degree is, the pulse number N needed is too large, making this method difficult to be realized in the experiment. In effect, though the contribution of M ≠ 0 rotational states to the molecular orientation is small compared with that of M = 0 rotational states, it still plays a role. As long as the population of the M = 0 rotational states (e.g. the | J, 0〉 rotational states) is in a proper proportion, a relatively high orientation degree can be obtained, which has been stated in Ref. [38]. Therefore, if we can rearrange the distribution of M = 0 rotational states, and meanwhile make the population of M ≠ 0 rotational states larger than their degenerate M = 0 rotational states, a good orientation effect can be achieved. What is more, it can be realized by adopting only a few linearly polarized laser pulses, thus reducing the pulse number.
 | Fig. 1. Initial distribution of the probability amplitude | CJ, M| of NO molecule at rotational temperature 10 K. |
To verify the above assumption, in the following, several linearly polarized resonant pulses will be adopted to rearrange the distribution of the m = 0 rotational states. Here, the electric field of the laser pulses adopted is given by
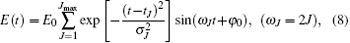
where ω J = 2J is the angular frequency of the pulse in resonance with the J − 1 ↔ J transition, σ and E0 are the duration and peak electric field amplitude of the laser pulses, and the initial phases of these pulses φ 0 are all set to be π .
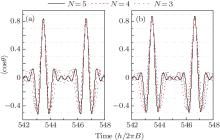
Here, the NO molecule whose rotational temperature is 10 K is taken as the computational example. We present in Fig. 2 the time-evolution of the probability amplitude | CJ, 0| under the actions of five linearly polarized resonant pulses whose durations are shown by the second row in Table 1. It can be seen from Fig. 2 that | CJ, 0| (J = 1, 2, 3, 4) first increase under the actions of pulse PJ and then decrease under the actions of pulse PJ+ 1. In contrast, | C0, 0| and | C5, 0| only decrease and increase under the actions of p1 and p5, respectively. After this operation, the distribution of the M = 0 rotational states is rearranged. Since the resonant excitation follows the selection rule of Δ J = ± 1, and Δ M = 0, the sum of the population of the M = 0 states is not changed during the above operation, which keeps 42.92%. The distribution of the probability amplitude | CJ, M| after this operation is shown in Fig. 3. As can be clearly seen from the figure, after being subjected to the 5 given pulses, the population of M ≠ 0 rotational states is smaller than that of their degenerate M = 0 rotational states. According to Eq. (4), the maximum orientation degree calculated is 〈 cos θ 〉 max = 0.8380 as shown by the solid black curve in Fig. 4(a). Though this value is a little smaller than that obtained in Ref. [37] (i.e. 〈 cos θ 〉 max = 0.907), it is still a relatively high value, and more importantly, the pulse number used is greatly reduced (N = 13 in Ref. [37]) and the circularly polarized pulses are not required, thereby making this scheme more feasible. If the pulse number is N = 4, and their durations are given in the second row of Table 2, the maximum orientation degree is 〈 cos θ 〉 max = 0.7898 as shown by the dashed red curve in Fig. 4(a). If we use three pulses whose durations are given in the second row of Table 3, the maximum orientation degree is 〈 cos θ 〉 max = 0.7281 [see the dotted blue curve in Fig. 4(a)], which is still a high value. It should be noted that the parameters listed in Tables 1– 3 are obtained by the following way: firstly, adjust the duration of pulse p1 until the orientation degree reaches its maximum value in this case; then adjust the duration of pulse p2 to pmax in turn so as to obtain the maximum orientation degree in each case; after adjusting the duration of pulse pmax, we adjust the duration of p1 − Pmax again. Such processes repeat until the orientation degree does not increase any more.
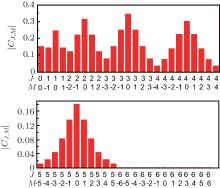 | Fig. 3. Probability amplitude | CJ, M| of the NO molecule after the actions of 5 linearly polarized pulses whose durations are shown in the second row of Table 1. |
| Table 1. Parameters of the 5 linearly polarized pulses used to obtain the maximum orientation degree for NO molecule at 10 K (first and second rows) and 5 K (first and third rows), respectively. |
| Table 2. Parameters of the 4 linearly polarized pulses used to obtain the maximum orientation degree for NO molecule at 10 K (first and second rows) and 5 K (first and third rows), respectively. |
| Table 3. Parameters of the 3 linearly polarized pulses used to obtain the maximum orientation degree for NO molecule at 10 K (first and second rows) and 5 K (first and third rows), respectively. |
In the above discussion, the rotational temperature is 10 K, in this case, the sum of the population of M = 0 states is 42.92%, and that of the M ≠ 0 rotational states is 57.08%. As stated in the previous part, the larger the sum of the population of M = 0 states, the higher the orientation degree will be. If the rotational temperature is reduced, the sum of the population of M = 0 states will become larger. Taking 5 K for example, the sum of the population of M = 0 states increases to 59.31% under this condition. Figure 4(b) shows the time-evolution of the molecular orientation degree of NO molecule 〈 cos θ 〉 at 5 K after the irradiations of 5 (solid black curves), 4 (dashed red curves), and 3 (dotted blue curves) linearly polarized pulses whose durations are shown in the third row of each of Tables 1, 2, and 3, respectively. It can be seen from the figure that the maximum orientation degrees achieved by adopting 5, 4, and 3 pulses are 0.8725, 0.8292, and 0.7599, respectively. If the rotational temperature is further reduced, the sum of the population of M = 0 states will be larger, and thus higher orientation will be obtained. In an extreme case, i.e., at a rotational temperature of 0 K, the molecular rotational state is populated only on the | 0, 0〉 state. In this case, under the actions of 4 pulses, the maximum orientation degree can be as high as 0.90612, which has already been discussed theoretically in Ref. [38].
As stated above, both the sum of the population of M = 0 rotational states and their distribution affect the maximum molecular orientation degree, however, the increase of the sum of the population of M = 0 rotational states is conducible to a little improvement in the molecular orientation degree. Even if the sum of the population of M = 0 states is not high, say in the case of the NO molecule at the rotational temperature of 10 K (the sum of the population of M = 0 states is only 42.92%), as long as the distribution of M = 0 rotational states is well rearranged, a good orientation effect can be achieved. Therefore, we arrive at such a conclusion that what mainly affects the molecular orientation is not the sum of the population of M = 0 states but their distribution.
In this study, we proposed a scheme to obtain a higher orientation degree starting from the NO molecule whose rotational temperature is higher than 0 K. It is found that both the sum of the population of M = 0 rotational states and their distribution affect the maximum molecular orientation degree, however, what mainly affects the molecular orientation is not the sum of the population of M = 0 states but their distribution. As long as the distribution of M = 0 rotational states is well rearranged, a relatively high orientation degree can be obtained. This process can be accomplished by just adopting several linearly polarized resonant pulses, and under the actions of these pulses the population of M ≠ 0 rotational states is smaller than that of their degenerate M = 0 rotational states. Through this scheme, molecular orientation degrees as high as 0.8380, 0.7898, and 0.7281 can be obtained under the actions of 5, 4, and 3 laser pulses at a rotational temperature of 10 K, which are relatively high molecular orientation degrees. However, the decrease of rotational temperature, i.e., the increase in the sum of the population of M = 0 states, is not helpful much to improve the molecular orientation. Though the pulse number used is not large, relatively high orientation degree can be obtained. Since the smaller pulse number is more suitable for the control of molecular orientation in the experiment, this scheme can be a promising approach.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|