Cite this Article
Galashev A. Y.†. Modeling the interaction of nitrate anions with ozone and atmospheric moisture. Chinese Physics B, 24(10): 103601  
Permissions
Modeling the interaction of nitrate anions with ozone and atmospheric moisture
Galashev A. Y.†
Institute of High Temperature Electrochemistry, Ural Branch, Russian Academy of Sciences, Yekaterinburg, Russia

†Corresponding author. E-mail: alexander-galashev@yandex.ru

Abstract

The molecular dynamics method is used to investigate the interaction between one–six nitrate anions and water clusters absorbing six ozone molecules. The infrared (IR) absorption and reflection spectra are reshaped significantly, and new peaks appear at Raman spectra due to the addition of ozone and nitrate anions to the disperse water system. After ozone and nitrate anions are captured, the average (in frequency) IR reflection coefficient of the water disperse system increased drastically and the absorption coefficient fell.

PACS: 36.40.Mr; 36.20.Ng; 92.70.Cp; 92.70.Er
Keyword: nitrate ion; ozone; water cluster; infrared and Raman spectra
1.Introduction

In the Earth’ s atmosphere, the ozone layer is situated at an altitude of 20 km– 30 km. The ozone layer protects life on Earth from being directly exposed to hard ultraviolet (UV) radiation. Since ozone is a greenhouse gas, its content in the troposphere affects the global climate. Oxidation of trace components is often treated as a self-purifying ability of the atmosphere. Although there is no definition of oxidizing ability, it is often associated with an excess of OH. However, many other oxidants, including O2 and O3, and free radicals different from OH, can contribute to the oxidation process taking place in the atmosphere. The radical is an important atmospheric oxidizer at night. The main mechanisms of decomposition are a reaction with organic components and heterogeneous losses (reactions on the Earth and on the surface of aerosol particles, including those in clouds). The gas-phase reaction between and water vapor is endothermic. Water vapor exerts a paramount influence on radiation transport in the troposphere.

Nitrate ions are some of the most widespread ions in the Earth’ s atmosphere. Their proportion exceeds that of atmospheric Cl– ions by more than 3.5 times and, by hundreds of times, that of Br– ions.[1, 2] Many atmospheric processes are explained by their presence. In Ref. [3], solvation of nitrate ions was studied at the air– water interface. A nitrate ion was shown to prefer surface solvation to bulk solvation. The lifetime of in the atmosphere depends on irreversible losses of N2O5, because thermodynamic equilibrium is established quickly between these two components. On the assumption that a stationary state is established during the decomposition of N2O5, the lifetime becomes inversely proportional to the NO2 concentration. Recently great attention has been paid to the investigation of the destructive effect that Cl– and Br– ions have on the content of atmospheric ozone, [2] whereas the effect of interaction between ions and ozone at the water surface has been elucidated in only a few studies.

Nitrate ions are generated in Earth’ s atmosphere in a chain of chemical reactions with nitric oxide. The nitrate ions are captured by aerosols, fall down with precipitation and become fixed in polar ice. Experimental investigation of the air-aqueous nitrate interface cannot completely provide an insight into the role of nitrate ions at the surface of aqueous-phase atmospheric aerosols. However, computer simulation to a certain extent gives such an understanding. Absorptions of ozone, oxygen, methane, and chlorine and bromine ions by atmospheric moisture are investigated in the molecular dynamics model.[4– 12] There are no data on how the presence of ions can change ozone absorption by water clusters or how nitrate ions influence the physical properties of the absorbing disperse water medium.

The aim of the present study is to investigate the simultaneous interaction of water clusters with nitrate ions and ozone molecules, and to reveal the behaviors of changes in spectral characteristics of disperse water systems, which result from such interactions.

2.Model

Properties of clusters and interfaces are not critically evaluated by using the original TIP4P potential model of water.[13] For this reason a new potential including an optimal set of parameters that describe the important properties of aqueous clusters (binding energies and minimum energy structures) has been developed.[14] It turned out that structure and thermodynamic properties of the bulk and liquid/vapor interface of water are also well reproduced by using a modified potential. A modification of the model fulfilled in Ref. [14] was connected with a considerable change in parameters of the Lennard-Jones (LJ) part of the potential; as a consequence, the coefficients with the terms describing repulsion and attraction were reduced by factors 2.5 and 2.9, respectively. Additionally, in this model, a negative charge was located at a point 0.0215 nm away from the oxygen nucleus instead of 0.015 nm as previously. This displacement allowed the permanent dipole moment of the water molecule to be corrected to 1.848 D, which corresponds to the experimental value in a gaseous phase. In the present work, a polarizable variant of the improved TIP4P model of water is employed.

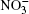
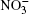
Interactions between nitrate ions and between water and ions are considered to be based on a polarizable model, proposed in Ref. [15]. The parameters of the potential for interactions were optimized so as to simulate the hydration energy and structural properties of a solvated nitrate ion. The molecular model of the ion represents a flat triangle with an N atom at the center and three O atoms at the corners. The angles between the bonds are identical and measured to be 120° , and the distance rNO = 0.122 nm. The partial electric charges of N and O atoms in the nitrate ion were determined to be qN = 0.5741e, qO = − 0.5247e (e is the elementary charge). As a whole, the ion showed the electric charge = − 1e. Quantum-mechanical calculations in the Hartree– Fock approximation determined the binding energy between the nitrate ion and water as 14.9 kcal/mol.[16] Electrostatic interactions between O3 molecules were determined by the charges qcen = 0.19e and qside = − 0.095e[17] placed at the points of localization of central and side atoms, respectively. The angle Oside– Ocen– Oside in the ozone molecule is 116.8° .[18] The distance between the central and some of the edge atoms in the O3 molecule is rOO = 0.1278 nm.

A pair of used atom– atomic potentials was treated as Lennard-Jones and Coulomb contributions. The parameters of the potential for the description of these interactions are given in Refs. [15] and [17]. In molecular dynamics calculations using the Stillinger– David polarization model, [19] the potential energy U of a cluster (H2O)50 took the value − 24.25 eV at T = 40 K.[20] In the model presented herein, the U value for the (H2O)50 aggregate is − 23.1 eV at T = 237 K.

The interaction of a water cluster with ozone molecules and nitrate ions was studied at the same temperature 237 K. Initially, the center of a free ozone molecule was located at a distance of 0.6 nm– 0.7 nm from the nearest center of the water molecule incorporated in the cluster. As this took place, the O3 molecule had a spontaneous orientation. Ions were brought to the system 6O3 + (H2O)50 in pairs and arranged on coordinate axes on different sides of the system at a distance of not less than 0.6 nm from any atom of the nearest molecule. The cutoff radius of molecular interactions in the model was 0.9 nm.

In the present work, we use a canonical ensemble simulation to calculate the spectral characteristics of water clusters.[21, 22] The molecular dynamics calculation is carried out in time steps of Δ t = 0.2 × 10− 16 s. The calculation of spectral characteristics is begun after the system has achieved an equilibrium state, which takes a time of tne = 3 × 105Δ t (6 ps). The (O3)6(H2O)50 cluster is also formed in ∼ 3 × 105Δ t time steps regardless of the presence of ions. The achievement of a steady value of the total dipole moment by this aggregate, along with obtaining a stable distribution of bond lengths, evidences the formation of the (O3)6(H2O)50 cluster. After the time tne expires, the dependence of the total energy of the system on time starts to fluctuate around the average value, which, along with the establishment of the Maxwellian velocity distribution, indicates that the equilibrium state is reached. From here on, we will take the beginning moment of the main calculation, that is, the moment when the system composed of water molecules, ozone, and nitrate ions has achieved equilibrium, is taken as the time origin (t = 0). The duration of the main calculation is comprised of 2.5 × 106Δ t time steps.

Flexible models of molecules are considered. Molecular flexibility is achieved by using the procedure designed within the framework of the Hamiltonian dynamics in Refs. [23]– [25]. In the model, each molecule can be considered as a polarizable point dipole situated in the center of mass of the molecule.[4– 12] The Gear fourth-order method is employed to integrate the equations of motion of centers of mass of molecules.[26] The analytical solution of motion equations for molecular rotation is accomplished by using the Rodrigues– Hamilton parameters; [27] and the integration scheme of motion equations considering rotations corresponds to the approach proposed by Sonnenschein.[28]

3.Dielectric properties

The absorption cross section of IR radiation is defined as[29]

where n is the frequency-independent refractive index, ε v is the vacuum dielectric permittivity, and c is the velocity of light.

In Eq. (1), the sum of vector differences of individual molecular dipoles is defined as

In the case of unpolarized light, the Raman spectra is given by the relation[29]

where

ω L is the frequency of an exciting laser, Π xz represents the xz component of the Π (t) value, the x axis is directed along the molecular dipole, and xy is the molecular plane.

The reflection coefficient R is defined as the ratio between the average energy flux reflected from the surface and the incident flux. At normal incidence of a plane monochromatic wave, the reflection coefficient is described by the formula[30]

It is supposed here that the incidence of a wave occurs from the transparent medium (medium 1) into a medium that can be either transparent or not, i.e., absorbing and scattering medium (medium 2). The indices of the dielectric permittivity in Eq. (2) refer to those of the medium.

We denote the systems as I (H2O)n, n = 10, 15, … , 50; 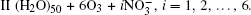The first system is composed of nine types of clusters, and the second one involves six types.

4.Results and discussion

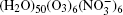
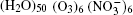
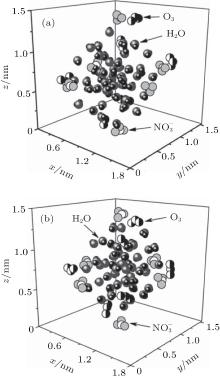The configurations of cluster formed by the time moments of 10 and 50 ps are shown in Fig. 1. From a comparison of these configurations one can conclude that the movements of all molecules and ions occurring in a confined space, i.e., movements associated with translational motion of the molecules are small. At the same time the orientations of molecules and ions vary quite significantly. From Fig. 1(a) it can be seen that the ions attract individual molecules H2O or O3. By the time 50 ps nearly all O3 molecules and ions are absorbed by the water cluster, with the major portion of O3 molecules being located in the immediate vicinity of the ions (Fig. 1(b)). The ions are attached to ozone molecules mainly due to the formation of N … Ocen bonds (here Ocen is the central atom in the ozone molecule), while ONO3 … H bonds are formed between them in close proximity to water molecules (ONO3 is the oxygen atom in the nitrate ion). The newly formed cluster remains as a whole undivided construction during all calculations.

Fig. 1. Configurations of the cluster 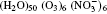corresponding to the time points of (a) 10 ps, (b) 50 ps at T = 237 K. Coordinates of molecules are given in nanometers.

Figure 2 displays IR absorption spectra for systems I and II, and it also shows the experimental IR spectra of liquid water[31] and spectra of O3[32] and HNO3, [33] which are present in the troposphere. The positions of the most intense bands in the IR spectrum for the water cluster system (system I) and in the spectrum of liquid water (3389 cm− 1 and 3404 cm− 1) correlate well with each other. The presence of ions and ozone molecules in the cluster system shifts the most intense band to the region of lower frequencies. With increasing the temperature of the water– ozone system containing anions, one can suppose that the inverse effect will emerge. When the temperature is increased to 287 K, i.e., by 50 K, the most intense band in the spectrum of system II moves 103 cm− 1 toward the region of high frequencies, and the intensity of this band decreases by 6.1%. A blue shift in absorption with rising temperature is caused by the weakening of the hydrogen bonding and structural correlation. These factors are both determined by spectral diffusion, [34] of which the essence lies in the fact that, with temperature rising, the transfer of quanta of OH-vibrations between the nearest oscillators is intensified. To put it differently, spectral diffusion is accounted for by the variation in vibration phases of modes typical of water. As a result of changes in the transfer of dipole vibrations, fluctuating forces appear, leading to the weakening of hydrogen bonds and the worsening of the structural correlation. This involves a rise in the intensity of the low-frequency portion of the IR spectrum (which is on the left of the most intense band).

Fig. 2. IR absorption spectra of the systems (i) I, (ii) II (for (i) and (ii) T = 237 K); (iii) liquid water (T = 293 K), the experiment; [31] (iv), (v) stratospheric measurements of O3[32] and HNO3, [33] respectively; (vi) system II at T = 287 K.

The most intense band in the IR spectrum of liquid water appears due to the superposition of three modes: ν 1 is the symmetric stretching vibration, ν 3 is the antisymmetric stretching vibration, and the overtone of a mode ν 2 is the deformation vibration (bending of covalent bonds). The mode ν 2 is responsible for the emergence of a band at 1644 cm− 1. The band at 690 cm− 1 is formed due to librations determined by restrictions imposed by hydrogen bonding. The weak band at 200 cm− 1 is associated with translation vibrations, including the stretching of the O– H … O hydrogen bond and its bending. At the IR spectrum of the water cluster system I, a blue shift of the libration mode by ∼ 380 cm− 1 with respect to the corresponding band in the IR spectrum of bulk water is observed. This band of system I is positioned between the positions of the second and the third peaks in the IR spectrum of stratospheric HNO3.

The IR spectrum of system II at T = 237 K shows three broad bands. The first one, of weak intensity, is localized at 748 cm− 1, the second, more intensive, band is at 1842 cm− 1, and the third one, most intensive, is located around 2936 cm− 1. The position of the first band agrees with quantum-mechanical calculation of localization of the mode of deformation vibrations (720 cm− 1) in the complex.[16] The second band occurs in the vicinity of the doubled frequency (1993 cm− 1) of the mode of antisymmetric vibration of ozone molecule, which was found empirically in Ref. [35]. The third band for the water cluster system containing O3 molecules and ions has a red shift with respect to the position (3389 cm− 1) of the most intense band in the IR spectrum of system I. The absorption band at ∼ 1058 cm− 1 for stratospheric ozone occurs due to the superposition of modes of symmetric and antisymmetric stretching vibrations (1063 cm− 1) in ozone.[35]

The work[36] showed that the absorption by (H2O)50 clusters of both molecular and monatomic oxygen yields a reduction in the integral intensity Itot of the IR absorption spectrum by a factor of 1.5– 2. In the course of the study, IR absorption spectra were calculated for the disperse water system III with nitrate ions , in which clusters adsorbed oxygen molecules rather than ozone molecules. The value Itot for system II (with ozone) appeared to be 1.6 times lower than that for system III (with oxygen). The capture of ozone by water clusters significantly reduces the ability to absorb IR radiation for the disperse water system.

The Raman spectra of systems I and II are represented by a great number of well-resolved peaks (Fig. 3). The three most intense peaks of system II fall at the frequencies of 938, 1941, and 3125 cm− 1. The most intense band in the Raman spectrum of disperse water system I is localized at 3040 cm− 1. The Raman spectrum of liquid water[37] shows the most intense band at 3337 cm− 1, and the Raman spectrum of complexes , N2O4 in a 78% water solution of HNO3[38] has a band at 1350 cm− 1. Bond type affects the shape of the Raman spectrum. For example, Raman shift, especially the radial breathing mode, is present in the spectrum of aqueous systems, but is generally absent from the spectra of graphite materials.[39]

Fig. 3. Raman spectra for the systems (i) I, (ii) II (for (i) and (ii) T = 237 K); (iii) liquid water (T = 293 K), the experiment; [37] (iv) Raman spectrum of the complexes and N2O4 in 78% water solution of HNO3[38] (for (iii) and (iv) T = 293 K).

Characteristic vibrations in liquid water occur with average intensities of 200 cm− 1 and 686 cm− 1. With allowance for anharmonicity of vibrations, one can expect that the sum of these modes will result in the occurrence of a band at the Raman spectrum localized around a frequency of 900 cm− 1. The intensity of the band at 938 cm− 1 in the Raman spectrum of system II increases with respect to the corresponding characteristic in the spectrum of system I (a band at 917 cm− 1). This increase occurs due to the influence of ions. Hydrated ions have a strong band in the Raman spectrum at 1049 cm− 1.[38] A band at 1941 cm− 1 at the J-spectrum of system II, on the one hand, can be considered as an analogue of the mode (2125 cm− 1) in liquid water resulting from the combination between the mode of deformation vibrations ν 2 and libration modes. On the other hand, ozone modes are represented as combinations of frequencies (2ν 3, ν 1 + ν 3, 2ν 1) in a range of 1993 cm− 1– 2143 cm− 1. Since the Raman spectrum of system I shows a very weak replica at 2048 cm− 1, the emergence of a strong band in the vicinity of this frequency in the Raman spectrum of system II can be attributed to the determining influence of ozone. The peaks at high frequencies (3040 cm− 1 and 3125 cm− 1) are likely to be caused by overtones of the mode of intense longitudinal vibrations, which appears in liquid water at 273 K in the form of the most intense band at 686 cm− 1, in combination with the mode of longitudinal vibrations at a frequency of 395 cm− 1 (the total frequency amounts to 3139 cm− 1).

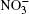
Figure 4 shows the frequency spectra of the reflection coefficient of disperse water systems I and II. The maximum of the R-spectrum of the system (I) of pure water clusters falls at a frequency of 1041 cm− 1, and that of the spectrum of the system (II) adsorbing ozone and nitrate ions localizes at 2882 cm− 1. The disperse water system I has an average (in frequency) IR reflection coefficient of R̄ = 0.35, while the same parameter for system II is 0.94. The spectrum R(ω ) for system I is fitted by a curve with a single pronounced peak, and the corresponding spectrum for system II is approximated by a frequency dependence with three peaks. Thus, homogeneous deposition of ozone molecules and nitrate ions onto the surface of (H2O)50 clusters produces high-efficiency reflection of IR radiation by the cluster system.

Fig. 4. Reflection coefficients of IR radiation for the cluster systems at T = 237 K: (a) system I, (b) system II; (i) MD calculations, (ii) approximation of the calculated dependence by the polynomial R(ω ) of the sixth order.

5.Conclusions

In the present work, the mechanism of adsorption of nitrate ions and ozone by water clusters is investigated. The initial orientation of surface water molecules in a cluster with hydrogen directed outwards produced an attractive force for 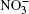ions. Since the initial distances between ions are more than twice those from ions to hydrogen atoms, ions move toward the cluster due to Coulomb attraction. Next, a heterocluster is formed due to Lennard-Jones interaction. Ozone molecules bearing small distributed electric charges do not hinder ions from attaching to the surface of the water cluster. Polarization interaction also creates a stabilizing effect. Eventually, in a time interval of 50 ps, negatively charged clusters with a water core are observed, with ions and ozone molecules situated at their surface.

Ozone is a very powerful oxidizer, much more powerful than oxygen. Therefore, the following processes should actually take place further at the surface of a cluster that has adsorbed ozone and ions. At the high concentrations observed, ozone decomposes into ordinary diatomic and monatomic oxygen. Under atmospheric conditions its half-life is approximately 30 min. Monatomic oxygen forms NO2 and O2 reacting with . Ultimately, nitrogen dioxide enters into a reaction with water and oxygen, producing nitric acid: 4NO2 (gas) + 2H2O (liq) + O2 ⇒ 4HNO3 (liq). A portion of NO2 can stay on the surface of the cluster formed by a water solution of nitric acid. Thus, the action of nitrate ions is similar to that produced by Cl– and Br– ions, destroying ozone at the water surface. Adsorptions of ions and ozone molecules by water clusters lead to a significant drop in the absorbing ability of the disperse water system. Water clusters with and O3 deposited on their surfaces reflect a major portion of the incoming IR radiation. Therefore, a smaller portion of the IR is trapped within the atmosphere. The greenhouse effect is reduced because of both lowering IR absorption by clusters and destroying ozone at their surfaces.

Reference
1 Golobokova L P, Latysheva I V, Mordvinov V I, Khodzher T V, Obolkin V A and Potemkin V L 2005 Atmos. Oceanic Opt. 18 616 [Cited within:1]
2 Foster K L, Plastridge R A, Bottenheim J W, Shepson P B, Finlayson-Pitts B J and Spicer C W 2001 Science 291 471 DOI:10.1126/science.291.5503.471 [Cited within:2]
3 Salvador P, Curtis J E, Tobias D J and Jungwirth P 2003 Phys. Chem. Chem. Phys. 5 3752 DOI:10.1039/b304537d [Cited within:1]
4 Galashev A E, Rakhmanova O R and Novruzova O A 2011 High Temp. 49 193 DOI:10.1134/S0018151X11010056 [Cited within:2]
5 Galashev A E, Rakhmanova O R and Novruzova O A 2011 High Temp. 49 528 DOI:10.1134/S0018151X11040080 [Cited within:1]
6 Galashev A E, Rakhmanova O R, Galasheva O A and Novruzov A N 2006 Phase Transitions 79 911 DOI:10.1080/01411590600968334 [Cited within:1]
7 Galashev A E, Chukanov V N, Novruzov A N and Novruzova O A 2006 High Temp. 44 364 DOI:10.1007/s10740-006-0046-7 [Cited within:1]
8 Galashev A Y 2010 Molecular Simulation 36 273 DOI:10.1080/08927020903307537 [Cited within:1]
9 Chukanov V N and Galashev A E 2008 Doklady Phys. Chem. 421 226 DOI:10.1134/S0012501608080095 [Cited within:1]
10 Novruzova O A, Chukanov V N and Galashev A E 2006 Colloid Journal 68 462 DOI:10.1134/S1061933X06040107 [Cited within:1]
11 Galashev A E, Rakhmanova O R Novruzova O A and Galasheva A A 2009 Colloid Journal 71 745 DOI:10.1134/S1061933X09060039 [Cited within:1]
12 Galashev A Y 2011 Can. J. Chem. 89 524 DOI:10.1139/V10-174 [Cited within:2]
13 Jorgensen W L, Chand rasekhar J, Madura J D, Impey R W and Klein M L 1983 J. Chem. Phys. 79 926 DOI:10.1063/1.445869 [Cited within:1]
14 Dang L X and Chang T M 1997 J. Chem. Phys. 106 8149 DOI:10.1063/1.473820 [Cited within:2]
15 Dang L X, Chang T M, Roeselova M, Garrett B C and Tobias D J 2006 J. Chem. Phys. 124 066101 DOI:10.1063/1.2171375 [Cited within:2]
16 Shem M, Xie Y, Schaefer H F and Deakyne C A 1991 Chem. Phys. 151 187 DOI:10.1016/0301-0104(91)80100-V [Cited within:2]
17 Hunt S W, Roeselova M, Wang W, Wingen L M, Knipping E M, Tobias D J, Dabdub D and Finlayson–Pitts B J 2004 J. Phys. Chem. A 108 11559 DOI:10.1021/jp0467346 [Cited within:2]
18 Nikol’skii B P 1966 A Chemist’s Hand book Leningrad Khimiya 1 337 [Cited within:1]
19 Stillinger F H and David C W 1978 J. Chem. Phys. 69 1473 DOI:10.1063/1.436773 [Cited within:1]
20 Vostrikov A A, Dubov D Yu and Drozdov S V 2008 Tech. Phys. Lett. 34 221 DOI:10.1134/S1063785008030139 [Cited within:1]
21 Galashev A Y 2013 Chin. Phys. B 22 073601 DOI:10.1088/1674-1056/22/7/073601 [Cited within:1]
22 Galashev A Y 2013 Chin. Phys. B 22 123602 DOI:10.1088/1674-1056/22/12/123602 [Cited within:1]
23 Lemberg H L and Stillinger F H 1975 J. Chem. Phys. 62 1677 DOI:10.1063/1.430718 [Cited within:1]
24 Rahman A, Stillinger F H and Lemberg H L 1975 J. Chem. Phys. 63 5223 DOI:10.1063/1.431307 [Cited within:1]
25 Saint–Martin H, Hess B and Berendsen H J C 2004 J. Chem. Phys. 120 11133 DOI:10.1063/1.1747927 [Cited within:1]
26 Haile J M 1992 Molecular Dynamics Simulation: Elementary Methods New York Wiley 161 [Cited within:1]
27 Koshlyakov V N 1985 Problems in the Dynamics of a Solid Body and the Applied Theory of Gyroscopes Moscow Nauka 16 [Cited within:1]
28 Sonnenschein R 1985 J. Comput. Phys. 59 347 DOI:10.1016/0021-9991(85)90151-2 [Cited within:1]
29 Bosma W B, Fried L E and Mukamel S 1993 J. Chem. Phys. 98 4413 DOI:10.1063/1.465001 [Cited within:2]
30 Land au L D and Lifshitz E M 1982 Course of Theoretical Physics. Electrodynamics of Continuous Media Moscow Nauka 8 407 [Cited within:1]
31 Goggin P L and Carr C 1986 Water and Aqueous Solutions Bristol–Boston Adam Hilger 37 149 [Cited within:1]
32 Wagner G, Birk M, Schreier F and Flaud J M 2002 J. Geophys. Res. 107 22 [Cited within:1]
33 Goldman A, Murcray F J, Blatherwick R D, Kosters J J, Murcray D G, Rinsland C P, Flaud J M and Camy-Peyret C 1992 J. Geophys. Res. 97 2561 DOI:10.1029/91JD02850 [Cited within:1]
34 Kraemer D, Cowan M L, Paarmann A, Huse N, Nibbering E T J, Elsaesser T and Miller R J D 2008 Proc. Natl. Acad. Sci. USA 105 437 DOI:10.1073/pnas.0705792105 [Cited within:1]
35 Rinsland C P, Flaud J-M, Perrin A, Birk M, Wagner G, Goldman A, Barbe A, Deacker-Barilly M R, Mikhailenko S N, Tyuterev Vl G, Smith M A H, Malathy Devi V, Benner D C, Schreier F, Chance K V, Orphal J and Stephen T M 2003 J. Quantum Spectrosc. Radiat. Transfer 82 207 DOI:10.1016/S0022-4073(03)00154-7 [Cited within:2]
36 Novruzova O A and Galashev A E 2008 High Temp. 46 60 DOI:10.1134/s10740-008-1009-y [Cited within:1]
37 Murphy W F 1977 J. Chem. Phys. 67 5877 DOI:10.1063/1.434794 [Cited within:1]
38 Kamboures M A, van der Veer W, Gerber R B and Phillips L F 2008 Phys. Chem. Chem. Phys. 10 4748 DOI:10.1039/b810081k [Cited within:2]
39 Wang H 2013 Chin. Phys. B 22 086301 DOI:10.1088/1674-1056/22/8/086301 [Cited within:1]