Ion-impact ionization of atomic and molecular systems is of particular importance in understanding the many physical phenomena occurring in various fields of science and technology.^{[1, 2]} The dynamics of such collisions can be studied in detail if their experimental fully differential cross sections (FDCSs) are available. Since it is very difficult to measure the scattered projectile momentum directly, such measurements are practically much more challenging. However, a recent development of the novel COLTRIMS technique, which stands for cold-target-recoil-ion-momentum spectroscopy, made it possible to perform the high-precession measurements of the FDCSs for ion-impact ionization processes.^{[3– 5]} Therefore this powerful technique provides the most sensitive tests of theoretical models describing few-body dynamics in charge transfer and ionization processes.

One of the reactions which has been experimentally studied by means of the COLTRIMS technique is the single ionization of ground-state helium atoms by fully stripped carbon ions.^{[6– 9]} This reaction has also been investigated using perturbative and non-perturbative sophisticated theoretical approaches. For example, the first-Born approximation (FBA), ^[10] three-body distorted wave (3DW), ^{[9, 11]} post and prior versions of the continuum distorted wave-eikonal initial state (CDW-EIS), ^{[12, 13]} correlated continuum wave-eikonal initial state (CCW-EIS), ^[14] fully quantum-mechanical convergent close-coupling (CCC), ^[15] coupled-pseudostate (CP), ^[16] and three-Coulomb wave (3CW)^{[17, 18]} approaches have been employed to study this process. Also, the experimental data reported on this reaction were analyzed with the second-Born approximation (SBA), ^[19] distorted-wave Born (DWB) model, ^[19] and time-dependent close-coupling (TDCC) approach.^{[20, 21]}

Despite the accounted theoretical studies of this subject, the dynamics of the specified ionization process is not complectly understood. This is due to the fact that the applied theoretical methods were not able to present a satisfactory description of all the aspects observed in the measured FDCSs for electron ejection into the scattering and perpendicular planes. This fact motivates further theoretical studies to achieve a consistent quantitative description of the collision dynamics.

In this paper, the first-Born four-body distorted wave approximation is utilized to analyze the single ionization of helium atoms in their ground states by impact of the fast bare carbon ions. In this method, which is referred to as the first-Born approximation with two Coulomb waves (FBA-2C), both the scattered projectile ion and the ejected electron are described by the Coulomb waves. The nine-dimensional integrals for the partial amplitudes are reduced to the closed-form analytical expressions or the one-dimensional integrals. The particular features of our analysis can be pointed out as follows. The model includes the passive electron both in the initial and final wave functions and in the perturbation potential. The role of the static electron correlations of the target atom on the ionization process has been investigated both in and out of the scattering plane. In comparison to the above-mentioned theories, the present numerical quadrature is very simple and extremely economic in time. In most of the considered cases, the obtained results are compatible with the much more complicated theories and even in some cases are in better agreement with the experiment. Specially, the method is successful in reproducing the peak structure observed in the experimental data.

The paper is organized as follows. In Section  2, the theory of the formalism is presented and the partial transition amplitudes for the considered process are evaluated. In Section  3, the obtained results are compared to the experiment. The concluding remarks are drawn in Section  4. Atomic units (ħ = e = m_e = 1), short as a.u., are used throughout the paper unless otherwise stated.

Let us consider a four-body collision system in which the fast bare ion P of charge Z_P and mass M_P impinges on an atomic target consisting of two active electrons e₁ and e₂ and a target ion T with nuclear charge Z_T and mass M_T. It is assumed that the collision process leads to the single ionization of the target atom. The two electrons are considered to be active during the collision. In the initial channel for such a reaction, the whole Hamiltonian can be decomposed to

where V_i is the perturbation potential. The prior form of the ionization amplitude is given by

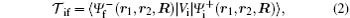
in which R, r₁, and r₂ denote the position vectors of the incoming projectile and the two bound electrons e₁ and e₂ with respect to the target nucleus. The perturbation potential V_i in the initial channel which is the part of the total interaction in the initial state is given by

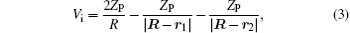
which vanishes at R → ∞ . Hence, there is no Coulomb distortion in the initial channel. Consequently, the initial wave function can be represented by

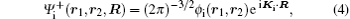
where K_i is the initial wave vector for the relative motion of P with respect to T in the center-of-mass (c.m.) frame and ϕ _i(r₁, r₂) is the initial bound state wave function of the target atom in its ground state. Since an exact bound-state wave function for the two-electron atomic target is not available, one can use different variational wave functions with different levels of accuracy to describe the initial state of the active electrons. Consequently, the obtained results for transition amplitude and the resultant cross section are possibly sensitive to a concrete choice of the wave function. In order to investigate this issue and for computational purposes, we assume that the initial bound-state wave function can be written as

in which cal and are the normalization constants and parameters ζ ₁ and ζ ₂ are known for the chosen wave function.

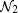
In the present approximation (FBA-2CW), both the scattered projectile ion and the ejected electron are described by the Coulomb waves. Also, it is assumed that the second electron, e₂, remains bound to the target nucleus T and is described by a ground-sate hydrogen-like wave function in its final state. This final bound state wave function is assumed as 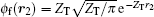. Then, the final-state wave function for the whole system can be approximated as

where ₁F₁ (a; b; z) is the confluent hypergeometric function, K_f is the final wave vector for the relative motion of P with respect to T in the c.m. frame, and k is the momentum vector for the ejected electron e₁. The Sommerfeld parameters are ν _PT = Z_PZ_e/K_f, and ν _T1 = − Z_e/k with Z_e as the effective nuclear charge of the residual target ion which is seen by projectile or ejected electron. 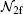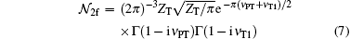The normalization constant is given by

in which Γ (z) is Euler’ s gamma function.

Inserting the explicit forms of the initial perturbation potential V_i, the undistorted initial and the distorted final wave functions into Eq.  (2), the nine-dimensional integral form of the transition amplitude is obtained. In fact the direct amplitude for the single ionization process is given by the sum of the three partial amplitudes corresponding to the different two-body perturbative interactions in the initial channel. Each partial amplitude is a nine-dimensional integral in the coordinate representation. Accordingly, the transition amplitude can be written as

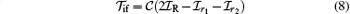
with (the asterisk refers to a complex conjugate). The partial amplitude is given by a nine-dimensional integral in coordinate representation as

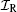
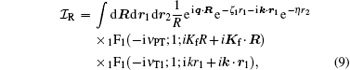
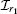
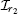
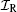
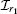
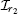
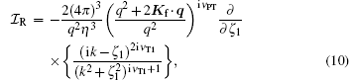
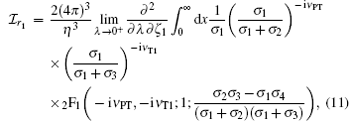
were η = ζ ₂ + Z_T, and the momentum transfer vector q is the difference between the incoming and the scattered projectile momentum, q = K_i − K_f. Also, the integral forms of and are given by similar expressions, but 1/R should be replaced by 1/|R − r₁| and 1/|R − r₂|, respectively. Using the Fourier transform technique and Nordsieck and Lewis integrals^{[22, 23]} and following the analytical analysis of Ghanbari– Adivi and Ghavaminia, ^{[24, 25]} it is possible to derive a closed-form expression for and to reduce and to some one-dimensional integrals. The details of the evaluation procedure are given elsewhere.^[26] Here, we give the final results

and

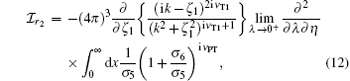
where ₂F₁(a, b; c; z) is the Gaussian hypergeometric function, and σ ₁, σ ₂, σ ₃, σ ₄, σ ₅, and σ ₆ are some functions of x:

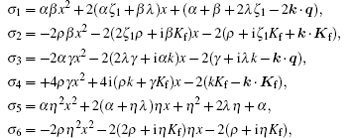
in which α = q² + λ ², 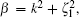γ = (k + iζ ₁)k, and ρ = i λ K_f − q · K_f.

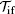
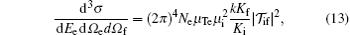
In the c.m. frame, the FDCS corresponding to the transition amplitude is given by

where dE_e is the energy interval of the ejected electron, dΩ _e and dΩ _f denote, respectively, the differential solid angles with respect to K_i for the ionized electron and the scattered projectile, and N_e is the number of the initial equivalent electrons in the atomic shell. μ _Te is the reduced mass of the ionized electron and the residual ion in the final channel, and μ _i is the reduced mass of the whole collision system in its initial channel.

In this section, we have computed the FDCSs for single ionization of the ground-state helium atoms by C⁶⁺ ions at impact energies of 2  MeV/amu and 100  MeV/amu. In order to examine the influence of the static electronic correlations of the two bound electrons of the atomic target on the cross sections, we used different wave functions to describe the initial bound states of the electrons. As the details were explained in Ref.  [26], these wave functions are referred to as the Hylleraas, Silverman, and Byron– Joachain wave functions. Further, our study shows that the cross sections are affected by the target ion effective charge Z_e that takes into account the presence of the passive electron. It is usual to consider the role of this factor on the ionization process by considering a dynamical effective charge to model the interaction between the projectile and the residual ion core.^[13] In our calculations, we set the effective nuclear charge as 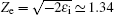, where ɛ _i is the binding energy for each of the electrons in their initial bound states.

Static correlation originates from the Coulomb interaction between the electrons before the collision takes place. Therefore the difference between an exact many-body structure calculation and the Hartree– Fock (HF) evaluations is a measure for this kind of correlation. Accordingly, the Hylleraas wave function is uncorrelated, but Silverman and Byron– Joachain wave functions are radially correlated. However, the last one is highly correlated because it gives a correlation energy which is very close to the exact value. All the formulas in the context are given for the c.m. system. But in order to make a direct comparison with the laboratory system of experimental measurements, the fully differential cross sections are presented for the laboratory system. The conversion from c.m. to the laboratory frame is given by a constant factor of 16 for present FDCSs.^[11]

For the impact energy of 2  MeV/amu, the calculations are carried out by Eq.  (13) for electron ejection into the scattering plane, which is defined by the initial and final momentum vectors of the incoming projectile ion and the obtained results are compared with their corresponding measurements reported in Ref.  [6]. The results are displayed in Figs.  1– 3. The CDW-EIS^[13] and 3CW^[18] theoretical results are also provided for comparison.

Fig.  1.

Figure Option ViewDownloadNew Window

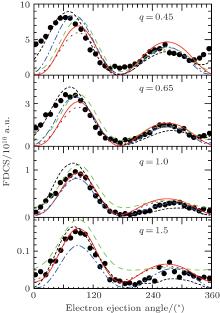Fig.  1. FDCSs in the scattering plane for 2-MeV/amu C6+ single ionization of helium. The ejected-electron’ s energy is 1  eV. The closed circles represent the experimental measurements.[6] The calculations are performed using the Silverman (solid), Hylleraas (dashed), and Byron– Joachain (dash– dotted) wave functions. The CDW-EIS (short-dashed)[13] and 3CW (dash– dotted)[18] results are also depicted for comparison.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Same as Fig.  1 but for ejected-electron’ s energy of 4  eV.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Same as Fig.  1 but for ejected-electron’ s energy of 10  eV.

In the CDW-EIS model, the electron– projectile interaction and the bound state of the active electron in the entrance channel are respectively described by an eikonal scattering phase factor and a semi-analytical Rothan– Hartree– Fock wave function. Also in the final channel, both projectile– ejected electron distortion and the wave function for the ejected electron in the field of the target residual ion are considered as Coulomb factors. Also, the perturbation potential is considered as an operator-type potential in the form of (the reader is referred to Ref.  [13] for more details). In the 3CW approach the final state wave function is described by a product of three Coulomb functions. Two Coulomb waves are for propagation of the projectile and the ejected electron in the field of the residual ion target and the third Coulomb factor is for the Coulomb interaction between the scattered projectile and the ionized electron. In a four-body version of the 3CW model the perturbation potential is the same as in the present work.^[18] As is seen from the figures, in the scattering plane, we notice a two-lobe structure in the angular distributions for all cases. The larger lobe, known as the “ binary peak” , results from the active electron being emitted in the direction of the momentum transfer q. This is due to a binary interaction between the projectile and the ejected electron where the ejected electron gives all of the transferred momentum; likewise, the second smaller lobe which occurs in the opposite direction of q known as the “ recoil peak” that is due to a double scattering process. In such a process the ejected electron is first struck by the incident ion and then scattered by the target nucleus. As is seen from the figures, the present calculations give a correct prediction of the magnitude and shape of the binary and recoil peaks in most of the specified cases.

As is seen from the figures, the calculated cross sections are a function of the static electronic correlation between the bound electrons in the target atoms. Therefore, the different wave functions lead to the different values for the FDCSs. The most static correlation dependence occurs around the binary peak. Also for larger values of the momentum transfer the difference between the results obtained from different wave functions becomes more considerable. This shows that the ionization cross sections are affected by the static correlations existing between the involved electrons in the process. Consequently a suitable description of this correlation can improve the theoretical results considerably.

For impact energy of projectile at 2  MeV/amu (Figs.  1– 3), although the shape of the angular distributions reproduced by the present theoretical calculations are all in acceptable agreement with the experimental results, in some angular regions there are some discrepancies between the calculations and the experiments. For example the results obtained using the Silverman wave function give a good description of the scattering process around the recoil peak, while in the binary peak region, there is a considerable discrepancy between the theory and experiments at smaller values of q. However, for a considered impact energy, as the momentum transfer increases to its larger values this discrepancy reduces and for larger values of q the theoretical results coincide with the experimental values to show a reasonable agreement. Anyway, at most of the scattering angles, as both the emission energy E_e and the momentum transfer q increase to their larger values, the magnitudes of the obtained cross sections approach to their experimental values. As may be seen from Figs.  1– 3, with increasing the ejected electron energy, the agreement between experiment and the FBA-2CW results will be better, especially in the angular region between 140° and 240° . Furthermore, it is worth noting that the recoil peak decreases as the electron ejection energy increases, and the present theoretical model predicts it correctly. Also in most of the considered cases the present results are fairly compatible with those obtained using the more complicated CDW-EIS^[13] and 3CW^[17] methods.

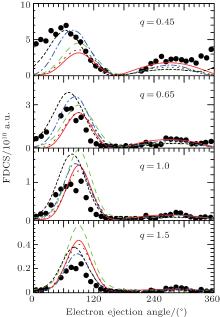
In Fig.  4, we present results for C⁶+ 100-MeV/amu single ionization of helium calculated in FBA-2CW, for the electrons emitted into the scattering plane with various values of the momentum transfer q and various emission energies E_k. The presented results are obtained using the different initial bound-state wave functions for the helium electrons. As is seen, there is a significant difference between the results obtained from different wave functions in the angular region around the binary peak. This means that the static electronic correlation plays an important role in the ionization process in this angular region. The results are compared with the experimental findings^[7] as well as the results obtained from the prior CDW-EIS^[12] and 3CW^[18] theories. As may be seen, most of the properties reported by these intricate models are also represented in our calculations. However our model is faster and more convenient relative to those theories. For all the cases, all the obtained results are in a reasonable agreement with the experiments in shape of curves. In other words, all of them can correctly predict the angular location of the binary peak. Particularly, the present results seem a little better than those of the 3CW approximation in the binary peak region. However, the situation is reversed when we compare the present model with CDW-EIS theory. The magnitude predicted by CDW-EIS for the binary peak is closer to the experimental findings in comparison with the present results.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. FDCSs in the scattering plane for 100-MeV/amu C6+ single ionization of helium. The values for the electron emission energy Ee and the momentum transfer q are given in the legends of the graphs. The symbols and lines are the same as those defined in Fig.  1. Experimental values and the CDW-EIS calculations are respectively taken from Refs.  [7] and [12].

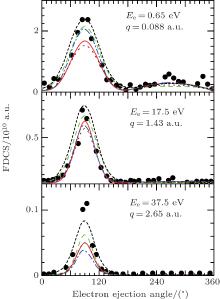
One of the puzzling aspects of the C⁶⁺ 100-MeV/amu ion single ionization of helium is the theoretical description of the FDCSs in the perpendicular plane. As is well known, the performed theoretical descriptions of the specified reaction cannot explain all the aspects exhibited in the experimental measurements for ejection of the electron into the perpendicular plane.^[8] The occurrence of the discrepancy between the theory and experiment refers to the incoherence property of the projectile beam used in the experiment, while the beam is described by a completely coherent wave function in theory. The FDCSs for ionization into the plane perpendicular to the incident beam direction are displayed in Fig.  5. The calculations are compared with the experimental values^[11] and with the 3DW^[9] and 3CW^[18] calculations. 3DW is the same as 3CW but the final-state wave function for the ejected electron is considered as a solution of the Schrö dinger equation with the distorting potential for the residual target ion.^[9] Also, 3DW is a three-body model while 3CW is a four-body one. As is seen from the figure, the static electron correlation can affect the cross sections especially at the angular region in which the peak structure occurs. In this region, the FBA-2CW is in a good agreement with the angular distribution of the measurements. For E_e = 6.5  eV and q = 0.88  a.u., the present results are compatible with those obtained from 3CW and 3DW theories. For E_e = 37.5  eV and q = 2.65  a.u., the present results are even better than those obtained from these more complicated theories.

Fig.  5.

Figure Option ViewDownloadNew Window

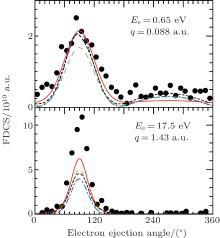Fig.  5. FDCSs in the plane perpendicular to the incident beam direction (containing the momentum transfer q) for 100-MeV/amu C6+ single ionization of helium. The solid circles are for the experimental measurements.[11] The results obtained from 3DW[9] (short-dashed) and 3CW[18] (dash– dotted) theories are also depicted in the figure. The solid and dashed lines are respectively obtained using the Hylleraas and Silverman wave functions.

A review of Figs.  1– 4 shows that the importance of the static electronic correlation in the ionization process depends on the ejected electron energy E_e as well as the momentum transfer q. For some values of E_e and q, the ionization is an uncorrelated process in some angular regions. Thus, the results obtained using the Hylleraas wave function are in better agreement with experiments. While in some other regions, the process is strongly correlated, subsequently the results of Byron– Joachain wave functions show a better harmony with the measured data. Also, there are some scattering regions that the correlation plays a moderator role and the Silverman wave function gives some better theoretical results.

A four-body first-order perturbation theory was applied to calculate the FDCSs for single ionization of helium atoms, both in and out of the scattering plane, by impact of the fast C⁶⁺ ions. The effects of the static electronic correlation on the ionization process were examined using the different initial bound-state wave functions for the electrons involved in the process. A comparison with the experimental values showed that the static electron correlation can play a main role in the ionization process particularly in the angular regions in which the peak structures occur. Also, our study showed that the effective nuclear charge Z_e can affect the calculated cross sections. Comparisons of the obtained results with their experimental values and with the results obtained from the more complicated theories such as 3CW, CDW-EIS, and 3DW showed that the proposed approach gives most of the aspects exhibited by the other theories and is in a reasonable agreement with the experiments. Similar to all the accounted theories, the outlined model treated the projectile beam as a completely coherent beam, while there are some aspects in the experimental data particularly in the perpendicular plane which originate from the incoherent nature of the projectile beam. Therefore, the theory has to consider the incoherent nature of the incident beam to improve the accordance of the results with the experimental measurements.