Cite this Article
Huang Tian-Shun†, Cheng Hai-Xia, Wang Xiao-Xu, Zhang Zhen-Feng, An Zhi-Wei, Zhang Guo-Hua. Site preferences and lattice vibrations of Nd6Fe13 − x T xSi ( T = Co, Ni) . Chinese Physics B, 24(10): 103402  
Permissions
Site preferences and lattice vibrations of Nd6Fe13 − x T xSi ( T = Co, Ni)
Huang Tian-Shun†a), Cheng Hai-Xiab), Wang Xiao-Xub),c), Zhang Zhen-Fengd), An Zhi-Weib), Zhang Guo-Huab)
Electric Engineering Department, Henan Vocatioanl & Technical College, Zhengzhou 450046, China
Department of Physics, Beijing University of Science and Technology, Beijing 100083, China
Department of Materials Engineering, National Ping Tung University of Technology and Science, Ping-Tung 91201, Taiwan, China
The 20 Middle School of Beijing, Beijing 100085, China

†Corresponding author. E-mail: tshuang09@163.com

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11272048 and 50971024) and the National Key Basic Research Program of China (Grant No. 2011CB606401).

Abstract

The site preferences of the rare earth intermetallics Nd6Fe13− x T xSi ( T = Co, Ni) are investigated by using interatomic pair potentials which are converted from a lattice-inversion method. Calculation shows that the order of the site preference of Co is 4 d, 16 k, 16 l1, and 16 l2 and that of Ni is 16 l2, 16 l1, 16 k, and 4 d in Nd6Fe13− x T xSi. Calculated lattice and positional parameters are found to agree with those reported in the literature. Furthermore, the phonon density of states for Nd6Fe13− x T xSi is also evaluated, and a qualitative analysis featuring the coordination and the relevant potentials is carried out.

PACS: 34.20.Cf; 61.66.Bi; 61.66.Dk
Keyword: interatomic potentials; site preference; lattice dynamics
1. Introduction

Over the past several years there have been many studies devoted to rare-earth transition-metal, R– M, compounds which contain silicon. Some of these silicon compounds are pseudobinary compounds, such as the R2M17− xSix and RM12− xSix compounds, [1– 5] and some are true ternary compounds, such as Nd6Fe13Si, in which silicon[6] is required to stabilize the crystal structure. The crystal structure of the R6Fe13− xM1 + x compounds (R = rare earth) was unraveled in 1985 by Sichevich et al.[7] They have shown that La6Co11Ga3 orders in a tetragonal structure with space group I4/mcm. Later, Allemand et al.[6] showed that Nd6Fe13Si crystallizes as an ordered variant of this compound. Both structure types are interesting from a technological point of view since their presence as the second phase in NdFeB-permanent magnets enhances the coercivity.[8] Experimentally, there have been studies of replacing Fe atoms in Nd6Fe13Si by other transition elements, and some of them had promising effects.[9, 10] The information about which crystalline site is actually replaced is helpful in understanding the mechanism of the property being changed by substitution. There have been numerous experimental studies devoted to identifying the site occupation.

However, sometimes the experiments do not clearly reveal which sites are substituted. Theoretical study should be a compensatory way to provide helpful information about the site substitution. In this paper, the interatomic potentials acquired by Chen’ s lattice inversion method are used to investigate the site preferences and lattice constants of these complicated compounds, Nd6Fe13− xTxSi (T = Co, Ni). In addition, the phonon densities of states (DOSs) of these rare earth intermetallics are evaluated, from which the corresponding Debye temperatures are obtained.

2. Calculation method

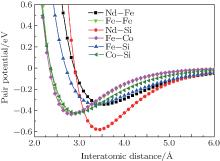
The acquisition of interatomic potentials prepares the groundwork for this research. According to Chen– Mö bius’ lattice inversion method, the intermetallic pair potentials can be inverted strictly from the cohesive energy curves.[11, 12] The methods of obtaining the interatomic pair potentials have been reported in detail.[13– 16] In this work, the inverted pair potentials from the cohesive energy are approximately expressed as Morse function

where D0 is the depth of potential, R0 is the equilibrium distance, and γ is a dimensionless parameter. For clarity, several important potentials are shown in Fig.  1.

Fig.  1. Potentials of Nd– Fe, Nd– Si, Fe– Si, Fe– Fe, Fe– Co, and Co– Si.

3. Results and discussion
3.1. Site preference

In this section, we first establish a theoretical structure of Nd6Fe13Si based on experimental one.[17] Then we study the substitution of Fe sites in this material by Co and Ni by computer simulation, and make comparisons with experiments where possible.

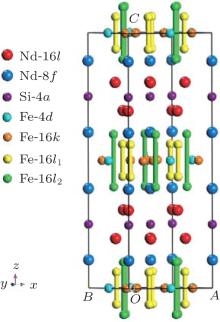
The Nd6Fe13Si-type structure can be described as a multilayer structure in which the layers are perpendicular to the tetragonal c axis. In Nd6Fe13Si the layers containing neodymium and iron are separated by layers containing only silicon on the 4a sites. The neodymium, which occupies the 8f and 16l sites, is found in layers adjacent to the silicon layer, and the layers of iron 4d, 16k, 16l1, and 16l2 sites are sandwiched between the neodymium layers. To illustrate it more clearly, the lattice cell of Nd6Fe13Si is shown in Fig.  2.

Fig.  2. Unit cell of Nd6Fe13Si.

According to experimental atomic sites of the model, [17] initial Nd6Fe13Si structure is constructed with the Accelrys Cerius 2 modeling software. In experiments, it is not easy to substitute elements with various concentrations. Since we have established the uniform and effective pair potential curves, we can numerically compute the effect of element substitutions for arbitrary concentration. We let the element T replace one of the four Fe sites, and optimize the crystal with a conjugate grads method, that is to say, relax the crystal until the cohesive energy reaches a minimum value. The relax system includes 2 × 2 × 2 = 8 crystalline cells. We take the average of 30 sample units for each substitution concentration.

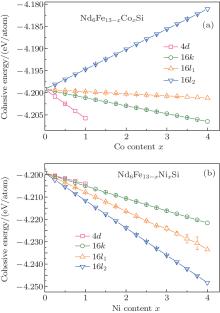
Figure  3 shows the cohesive energy of the Nd6Fe13− xTxSi as a function of the T content, and the error bars in the figure represent the ranges of the root mean square errors. For x ≤ 0.34, the energy is the lowest with Co atoms entering into the 4d sites of the hexagonal structure. Therefore, the Co atoms will preferentially occupy the 4d sites of Nd6Fe13− xCoxSi compounds. For Nd6Fe13− xNixSi, Ni atoms entering into the 16l2 sites have the lowest energy. So Ni atoms should prefer the 16l2 sites with the space group I4/mcm for Nd6Fe13− xNixSi compounds. The calculated results show that the preferential occupation sequence for Co is 4d, 16k, 16l1, and 16l2, and that for Ni is 16l2, 16l1, 16k, and 4d in Nd6Fe13− xTxSi.

Fig.  3. The calculated values of cohesive energy of Nd6Fe13− xTxSi (T = Co, Ni) compounds.

Table 1. Lattice parameters a and c of Nd6Fe13− xTxSi in unit Å .

According to the results for the occupancy behaviors of T, the lattice parameters of the Nd6Fe13− xTxSi are calculated when T atoms are in 4d or 16l2 sites. Table  1 shows the results of Nd6Fe13− xTxSi obtained from both the experiments[9, 17] and calculation. Atomic parameters have also been investigated based on the inverted pair potentials (Table  2). The calculated atomic parameters of Nd6Fe13− xTxSi are close to experimental results.[17] The differences between the experimental and calculated lattice and positional parameters are at most 2.00%, which is quite acceptable.

Table 2. Positional parameters in Nd6Fe13Si at 17  K and 295  K.

Furthermore, the structural property is to be simulated by the high temperature disturbance test with molecular dynamics to check the lattice constants and phase stability at high temperature. We thus perform molecular dynamics simulations at constant pressure and temperature (NPT, where N denotes the number of particles, P the pressure, and T the temperature). For constant-NPT molecular dynamics the temperature and pressure are kept constant with using an extended system with a thermostat and barostat relaxation time of 0.1  ps. The simulation temperature range is 0  K– 900  K. For each temperature and at 1  atm (1  atom = 1.01325× 105  Pa), pressure calculations are performed for 5 × 104 steps in time steps of 2.0× 10− 15  s. After equilibrium is reached, the crystal symmetry remains in the initial I4/mcm space group. The lattice and positional parameters for Nd6Fe13− xTxSi can also be obtained and are given in Tables 1 and 2. From Tables  1 and 2, one can see that our results for Nd6Fe13− xTxSi at difference temperatures are in agreement with experimental results, [17] which means that the applicability of the present interatomic potential is well proven by demonstrations.

3.2. Lattice dynamic simulations

Starting with the effective interatomic potentials and lattice dynamics theory, we calculate the total DOS and the partial DOS projected to different elements in Nd6Fe13− xTxSi. The calculated results are shown in Fig.  4. The DOS of Fig.  4 is calculated by adding up 936 k points in 1/8 the first Brillouin zone of a simple tetragonal lattice. The cut-off distance of force constants is set at 6  Å . It is estimated that the cut-off frequencies of the vibrational modes are 9.12 (Nd6Fe13Si), 9.02 (Nd6Fe12CoSi), 9.01 (Nd6Fe11Co2Si), 9.14 (Nd6Fe12NiSi), and 9.17 (Nd6Fe11Co2Si) THz, respectively. From the partial DOS, it can be inferred that the vibrational modes above 3.00  THz are mostly excited by Fe. Rare earth Nd atoms contribute a major part to the modes with lower frequencies. The Si atom only contributes to three optically localized modes around 6.8, 7.0, and 8.0  THz.

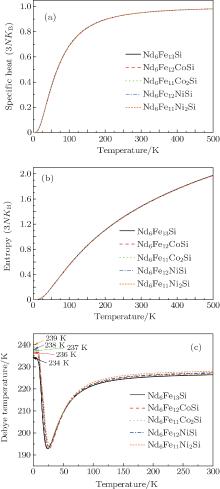Fig.  4. Phonon DOSs of Nd6Fe13− xTxSi (T = Co, Ni) compounds.

Fig.  5. Calculated values of specific heat, vibrational entropy, and Debye temperature of Nd6Fe13− xTxSi (T = Co, Ni) compounds.

In this work, the localized modes are analyzed qualitatively from interatomic potentials in Fig.  1. We take Nd6Fe11Co2Si for example. Since the curve Φ Nd − Si(r) is deep and narrow, Nd atoms react quite strongly with the nearest-neighbor Si atoms. The mass of the Nd atom is approximately five times that of the Si atom, so the Nd atoms are assumed to be motionless relative to the Si atoms. Then the Si atoms are restricted by the Nd atoms in the ‘ potential well’ Φ Nd − Si(r) and excite the local modes which correspond to the higher frequencies. For Nd atoms, they only contribute to lower frequency vibrations in the Nd-Si ‘ potential well’ because of their large atomic mass. The distances between Fe (16l2) and its nearest Fe atoms at the Fe (16k) or (16l1) sites are within 2.501  Å – 2.711  Å . From Fig.  1, it can be seen that the interactions between Fe and Fe at these distances are very strong, which results in a restriction that causes Fe to vibrate at the total frequency. As shown in Fig.  1, the Fe– Fe interaction is nearly the Co– Fe interaction. Hence, the frequency modes of the Co are almost the same as those of the Fe in shape, but the amplitudes are much smaller because the quantity of ternary elements is small.

Figure  5 gives the calculated values of lattice specific heat and vibrational entropy of Nd6Fe13− xTxSi. The figure clearly shows that the variations of specific heat and entropy with temperature for the ternary systems do not show any anomaly. The calculated Debye temperature of Sm2Fe15Mn2 is also shown in Fig.  5. The values of Nd6Fe13Si, Nd6Fe12CoSi, Nd6Fe11Co2Si, Nd6Fe12NiSi and Nd6Fe11Co2Si are 234, 236, 237, 238, and 239  K near 0  K, respectively. The changes of Debye temperature are relatively small when the T atoms substitute Fe atoms in the Nd6Fe13Si compound.

4. Summary

In this work, the site occupancies of Fe and Co in Nd6Fe13Si are investigated by interatomic potentials which are converted from the Chen– Mö bius’ lattice-inversion method. The calculated cohesive energy of Nd6Fe13− xTxSi shows that the preferential orders of T = Co and Ni are 4d, 16k, 16l1, 16l2, and 16l2, 16l1, 16k, 4d, respectively. The calculated lattice and positional parameters are in good agreement with observed results from the literature. In addition, we utilize the inversion pair potentials to evaluate the phonon density of states of Nd6Fe13− xTxSi, and obtain its specific heat, vibrational entropy and Debye temperature.

Reference
1 Long G J, Marasinghe G K, Mishra S, Pringle O A, Grand jean F, Yelon W B, Pourarian F and Isnard O 1993 Solid State Commun. 88 761 DOI:10.1016/0038-1098(93)90872-K [Cited within:1]
2 Artigas M, Fruchart D, Isnard O, Miraglia S and Soubeyroux J L 1999 J. Alloys Compd. 291 282 DOI:10.1016/S0925-8388(99)00277-7 [Cited within:1]
3 Isnard O and Buschow K H J 1997 J. Alloys Compd. 267 50 DOI:10.1016/S0925-8388(97)00539-2 [Cited within:1]
4 Buschow K H J 1988 J. Appl. Phys. 63 3130 DOI:10.1063/1.340865 [Cited within:1]
5 Solzi M, Pareti L, Moze O and David W I F 1988 J. Appl. Phys. 64 5084 DOI:10.1063/1.342437 [Cited within:1]
6 Allemand J, Letant A, Moreau J M, Nozières J P and Perrier de la Bâthie R 1990 J. Less-Common Metal 166 73 DOI:10.1016/0022-5088(90)90367-S [Cited within:2]
7 Sichevich O M, Lapunova R V, Soboley A N, Grin Yu N and Yarmulek Ya P 1985 Sov. Phys. Crystallogr. 30 627 [Cited within:1]
8 Schrey P and Velicescu M 1991 J. Magn. Magn. Mater. 101 417 DOI:10.1016/0304-8853(91)90800-P [Cited within:1]
9 Iranmanesh P, Tajabor N, Rezaee Roknabadi N, Pourarian F and Brück E 2011 Intermetallics 19 682 DOI:10.1016/j.intermet.2011.01.006 [Cited within:2]
10 Iranmanesh P, Tajabor N and Pourarian F 2013 Intermetallics 42 180 DOI:10.1016/j.intermet.2013.06.004 [Cited within:1]
11 Chen N X and Ren G B 1992 Phys. Rev. B 45 8177 DOI:10.1103/PhysRevB.45.8177 [Cited within:1]
12 Chen N X, Chen Z D and Wei Y C 1997 Phys. Rev. E 55 R5 DOI:10.1103/PhysRevE.55.R5 [Cited within:1]
13 Cheng H X, Wang X X, Hu Y W, Zhang G H, Shen J, Qian P and Chen N X 2015 J. Solid State Chem. 224 7 DOI:10.1016/j.jssc.2014.02.015 [Cited within:1]
14 Wang X X, Qian P, Zhang Z F, Liu Y, Shen J and Chen N X 2013 Intermetallics 42 112e119 DOI:10.1016/j.intermet.2013.05.0122013 [Cited within:1]
15 Li J C, Qian P, Zhang Z F, Yuan X J, Wang Y W, Shen J and Chen N X 2013 J. Solid State Chem. 201 250 DOI:10.1016/j.jssc.2013.03.002 [Cited within:1]
16 Qian P, Hu Q Y, Shen J, Feng Y, Pan H Y and Hu P 2010 Model. Simul. Mater. Sci. Eng. 18 045002 DOI:10.1088/0965-0393/18/4/045002 [Cited within:1]
17 Isnard O, Long G J, Hautot D, Buschow K H J and Grand jean F 2002 J. Phys. : Condens. Matter 14 12391 DOI:10.1088/0953-8984/14/47/313 [Cited within:5]