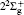In this section we only present the basic technique of the QMOCC method for the present collision system. A more detailed account of the description can be found in Refs.  [8] and [9]. In the QMOCC method, a coupled set of second-order differential equations was solved by the log-derivative method.^[13] The radial and rotational (A^r and A^θ ) couplings are responsible for driving the transition between channels. Considering the interchange of the two identical nuclei, the electron wave function has gerade (g) and ungerade (u) manifolds. The coupled sets of differential equations are solved separately for the g- and u-states and matched to the plane-wave boundary conditions. By the obtained S^{g, u} matrices, the scattering amplitudes of the g- and u-channels can be expressed as the following standard form:^[8]

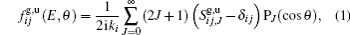
where k_i denotes the initial momentum for center-of-mass motion, J is the total angular momentum quantum number, and P_J is the Legendre polynomial of order J.

The cross sections are given for direct scattering and charge transfer by the following expressions:

respectively, where the S matrices are given by

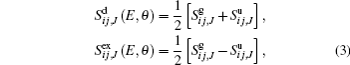
corresponding to the direct scattering and charge transfer processes.

The details of the two-center AOCC methods can be found in the literature, ^{[8, 12]} which we shall only outline briefly. The total electron wavefunction is expanded in terms of bound atomic orbitals of the two ionic centers, (ϕ ^A, ϕ ^B), multiplied by plane wave ETFs,

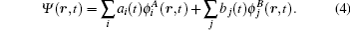
For the Li⁺ ions, the frozen core approximation is employed. The interaction between the active electron and the ionic cores is expressed by model potential^[5] (for Li⁺ ions)

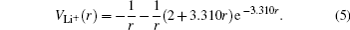
Adopting the straight-line approximation for nuclear motion, and substituting the expansion  (4) into the time-dependent Schrö dinger equation, we can obtain the first-order coupled equations:

where A and B are the vectors of the amplitudes a_i and b_j, respectively; S is the overlap matrix (S^† is its transposed form); H, , and K, are the direct and exchange coupling matrices.

By integrating corresponding translational probabilities over the impact parameter, the cross section for charge transfer can be obtained by

In our AOCC calculations for the present collision system, the projectile basis includes all atomic states with n ≤ 4, while on the target all n ≤ 3 bound states are included in the basis.

For the molecular structure calculations of the Li⁺ − Li(2s) system, the potential produced by the core electrons and the Li atomic nuclei is usually replaced by the pseudopotential or model potential. In the present study, both the all-electron model (AEM) and one-electron model (OEM) are used in the ab initio MRDCI, ^{[10, 11]} calculations for the potential energy curves of the five lowest , five , three ²Π _g, and three ²Π _u electronic states of the molecular ion. The subscripts g and u represent the asymmetric and anti-symmetric combinations of the electron wave functions for the exchange of the two lithium nuclei. In OEM, all the inner-shell electrons are frozen and only the valence electron (2s for Li) is considered in the ab initio self-consistent field (SCF) and CI calculations. For the Li atom, a (2s1p2d) diffuse set adding to the cc-pVTZ type basis set^[14] are employed. The differences between the present calculated asymptotic energies and the experimental results^[14] are less than 210  cm^{− 1}. The radial and rotational couplings are then calculated with the obtained electronic wave functions by using the finite differential and analytical methods, respectively.^[16] In this work, the translational effect was taken into account by introducing the common translation factors with the method of Bacchus– Montabonel.^[17]

Potential energy curves of the ion calculated with AEM and OEM are presented in Figs.  1(a) and 1(b), respectively, in the internuclear distances of R = 0.9  a.u.– 30  a.u. (the unit a.u. is the atomic unit). The and states, corresponding to [Li⁺ + Li(2s)] and [Li(2s) + Li⁺ ] asymptotic (R = ∞ ) configurations, represent the initial channels for the Li⁺ − Li(2s) collisions. At low collision energies, the collision process can be treated as a two-state problem because the and states do not couple with upper states. The resonant charge transfer would be the dominant inelastic process under these conditions. The translation probability is determined by the interference between the gerade and ungerade scattering amplitudes.^[8]

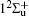
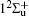
In Table  1, we present the values of equilibrium distance R_e and the depth of potential well D_e of the present calculated states. Our results are also compared with the available theoretical calculations.^{[7, 18– 20]} It can be observed that the present calculated spectroscopic constants with AEM and OEM are both reliable and agree well with each other for the ground state and the low-lying energy states. 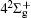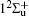For the high-energy states such as , , and 2²Π _g, some discrepancies can be found between the results acquired from the two models. However, such discrepancies would have a limited influence on the dynamics calculations, since the resonant charge transfer between and is the dominant process in the collision system for the considered collision energies in this work.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Curves of potential energy versus internuclear distance R of the molecular ion. (a) AEM; (b) OEM.

Table 1.

Table 1.

Table 1. Values of equilibrium position Re (a.u.) and depth of potential well De (eV) for the lowest states of . State Present work Ref.  [18] Ref.  [19] Ref.  [20] Ref.  [7] AEM OEM Re De Re De Re De Re De Re De Re De 5.90 1.293 5.90 1.278 5.98 1.26 5.90 1.31 5.94 1.24 5.89 1.248 13.0 0.306 13.0 0.304 13.0 0.31 12.8 0.30 21.0 0.369 21.0 0.366 22.0 0.37 29.0 0.183 29.0 0.175 28.0 0.14 19.0 0.0116 19.0 0.0111 19.0 0.011 18.0 0.011 25.0 0.0160 25.0 0.0150 25.0 0.016 24.0 0.014 37.0 0.0219 38.0 0.0187 42.0 0.0552 45.0 0.0497 22Π g 35.0 0.052 36.5 0.0459 12Π u 7.50 0.255 7.50 0.249 7.60 0.25 7.60 0.35 8.26 0.17 22Π u 18.5 0.345 19.0 0.332 19.5 0.37

Table 1. Values of equilibrium position Re (a.u.) and depth of potential well De (eV) for the lowest states of .

The radial coupling matrix elements are shown in Fig.  2 for the g-states (Fig.  2(a)) in the all-electron model and Fig.  2(c) in the one-electron model) and u-states (Fig.  2(b) in the all-electron model and Fig.  2(d) in the one-electron model) of the system with the electron translation factors included. We can see that the results of the all-electron model and the one-electron model are very similar except for the couplings between the higher states at small internuclear distances. This would have some influence on the cross sections only in the high collision energy region. The and states do not couple with upper states strongly until R < 5  a.u. This means that the state couplings would only influence the resonant charge transfer process at very high energies. The two-state approximation would be adequate in the low energy region.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Radial coupling matrix elements between the g-states (panels (a) and (c)) and between the u-states (panels (b) and (d)) of .

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Rotational coupling matrix elements between the g-states ((a) and (c)) and between the u-states ((b) and (d)) of .

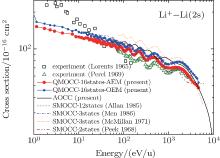
The present resonant charge transfer cross sections calculated by the QMOCC method in an energy range of 1.0  eV/u– 5000  eV/u, and by the TC-AOCC method in an energy range of 100  eV/u– 10⁴  eV/u are shown in Fig.  4. In the same figure, we also show Lorents et al.’ s^[1] and Perel et al.’ s^[2] experimental results, as well as Allan and Hanssen’ s theoretical results.^[6] obtained with the 12-state SMOCC method, Men et al.’ s^[7] and McMillan’ s^[5] 3-state SMOCC results, and Peek et al.’ s^[4] 2-state SMOCC results. The results of the present QMOCC calculations (AEM and OEM) and AOCC calculation agree well with each other at energies around 1  keV/u, where the two theoretical methods are both reliable.

Our OEM results are slightly larger than those of the AEM calculation in the whole energy range. For energies below 1  keV/u the relative discrepancies between the results of the two models are within 12%, however, with increasing collision energies the relative discrepancies will increase. This is because the cross sections sensitively depend on the accuracy of the molecular structures, and at small internuclear distances their OEM and AEM calculations are slightly different from each other. For energies below 1  keV/u the OEM calculation can also give a reliable prediction of the resonant charge transfer cross sections for the Li⁺ − Li collision system, while at energies above 1  keV/u it becomes unreliable since the model potential and pseudopotential energies lack the repulsive core which becomes important in the high-energy region.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Plots of resonant charge transfer cross section versus energy for Li+ − Li(2s) collisions.

Our QMOCC and AOCC calculations also agree well with most of the other theoretical results.^{[4– 7]} The charge transfer cross sections decrease with the increasing of energy, but all of the experimental and theoretical results show oscillation structures in an energy range of 10  eV/u– 5000  eV/u. The potential energy curves at small internuclear distances critically influence the forms of these oscillations, which results from the collisions at small impact parameters. The three-state results of McMillan^[5] are larger than other calculations. This may arise from their inaccurate molecular structures, as we have noted that the magnitudes of the cross sections depend sensitively on the molecular structure calculations. For energies above 1  keV/u, serious discrepancies can be observed between the SMOCC results of Peek^[4] and other calculations. This may be due to the two-state approximation used in their SMOCC calculation. The inelastic transition at small internuclear distance (see Figs.  1– 3), which has been proved to be important for the results in the high collision energy region, was not taken into account in their calculations. Men et al.^[7] also performed the two-state calculation and showed that the two-state and three-state results have similar magnitudes, but the frequencies of the oscillation structures are different at about E > 200  eV/u.

For energies above 20  eV/u, the present AEM cross sections agree well with the experimental measurements, ^{[1, 2]} with no more than 20% discrepancies. The oscillatory structures measured by Perel et al.^[2] are very well reproduced in our calculations. For energies below 20  eV/u, the resonant charge transfer cross sections measured by Lorents et al.^[6] are quite different from ours and other theoretical results.^[1] More accurate absolute experiments are desirable to resolve this remaining question.