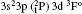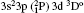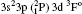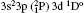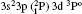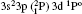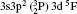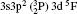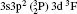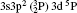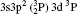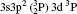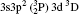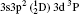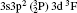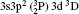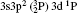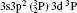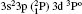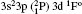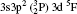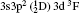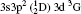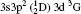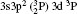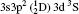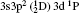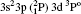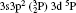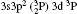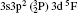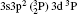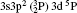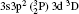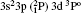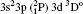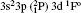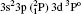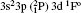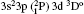Cite this Article
Khatri Indu, Goyal Arun†, Aggarwal Sunny, Singh A. K., Mohan Man. Extreme ultraviolet and x-ray transition wavelengths in Rb XXIV. Chinese Physics B, 24(10): 103202  
Permissions
Extreme ultraviolet and x-ray transition wavelengths in Rb XXIV
Khatri Indua), Goyal Arun†a), Aggarwal Sunnya),c), Singh A. K.b), Mohan Mana)
Department of Physics and Astrophysics, University of Delhi, Delhi-110007, India
Department of Physics, D.D.U. College, University of Delhi, Delhi-110015, India
Department of Physics, Shyamlal College, University of Delhi, Delhi-110032, India

†Corresponding author. E-mail: arun.goyal.du@gmail.com

*The authors, Indu Khatri and Arun Goyal, were supported by the U. G. C., India for their Junior Research Fellowship and Man Mohan by the U.G.C. for Basic Science Research Fellowship.

Abstract

Energy levels, radiative rates, oscillator strengths and line strengths are reported for transitions among the lowest 97 levels of the (1s22s22p6) 3s23p2, 3s23p3d, 3s3p3, 3p4, 3s3p23d, and 3s23d2 configurations of Rb XXIV. A multiconfiguration Dirac–Fock (MCDF) method is adopted for the calculations. Radiative rates, oscillator strengths, and line strengths are provided for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions from the ground level to all 97 levels, although calculations are performed for a much larger number of levels. To achieve the accuracy of the data, comparisons are provided with similar data obtained from the Flexible Atomic Code (FAC) and also with the available theoretical and experimental results. Our energy levels are found to be accurate to better than 1.2%. Wavelengths calculated are found to lie in EUV (extreme ultraviolet) and x-ray regions. Additionally, lifetimes for all 97 levels are obtained for the first time.

PACS: 32.70.Cs
Keyword: atomic data; energy levels; transition probability
1. Introduction

The studies of stellar and solar coronae have been intensified as a result of superb coronal spectra recorded by extreme ultraviolet (EUV) explorer satellite, the Chandra x-ray Observatory and the Solar Heliospheric Observatory (SOHO).[1, 2] As satellite-borne telescopes and instruments have expanded the range of detectable radiations into the x-ray region, astrophysical interest in the spectra of multiply charged ions has increased. The Ultraviolet (UV) through EUV and soft x-ray emission lines are useful for providing detailed knowledge about coronal atmosphere. Stellar coronal spectra are found to be rich in emission lines from high ionization states of highly ionized species[3] of cosmically abundant elements such as C, Mg, Si, Fe, and Ni which radiate in the x-ray region.[4]

There is considerable interest in the accurate atomic data for highly stripped ions as excitation energies and oscillator strengths in these ions are helpful in estimating the energy loss through impurity ions in fusion plasmas, diagnostic determination and modeling of high temperature astrophysical and laboratory plasma[5– 7] and also in determining the stellar envelope opacities.[8] Precision spectroscopy also requires accurate theoretical values both for astrophysical and beam foil measurements. An accurate determination of radiative transition properties for highly ionized Si-like ions are important as a number of these have been observed in solar corona, in tokamak discharges and in laser produced plasma. Emission lines from singly and multiply charged Si-like ions have been observed in solar corona and laser produced plasmas.[9– 12] Moreover, lines from intercombination transitions in Si-like ions are found to be useful in understanding density fluctuations and other elementary processes occurring in interstellar and laboratory plasma.[13, 14] Though silicon-like ions have been studied theoretically and experimentally, semi empirical methods with limited predictive power and accuracy have been employed to evaluate energy levels. Most of the studies of the ions of the Si-isoelectronic sequence, available in the literature, are limited to transitions involving few low lying states of the n = 3 subshell.[15– 48]

There are only limited data available for Si-like Rb based on semi empirical methods. Huang, [20] performed fully relativistic ab initio calculations of energy levels and transition probabilities for 27 low lying levels of Si-like ions in a range of Z = 15– 106 by using a multiconfiguration Dirac– Fock (MCDF) method. A systematic study of atomic binding energies of ground state configurations for the lithium-to-dubnium isoelectronic series was performed by Rodrigues et al.[49] Thomas et al.[50] calculated the ionization potentials for all the elements up to Z = 103 based on a simple spherical shell solution for neutral atoms. Wavelengths and transition rates for magnetic-dipole transitions (M1) within 3s23pn ground configurations of ionized Cu-to-Mo were predicted by Sugar and Kaufman.[51] Khan[42] observed the Si-like spectra of Cu-to-Mo in tokamak-generated plasmas, and Cu-to-As in laser-produced plasmas. Though the spectrum of Rb was not observed, from the rest of the data the interpolated values of wavelengths were derived for Si-like Rb. Bié mont et al.[52] derived new ionization potentials for many light ions (3 ≤ Z ≤ 50) by systematically considering the differences in the calculated ab-initio value among these potentials. A semi-empirical jj-relativistic approach was used to check the consistency among the published experimental values of the p2, p3, and p4 isoelectronic sequences including the Si sequence.[53] Charro et al.[27] calculated oscillator strengths of 3s23p2– 3s23p3d and 3s23p2– 3s23p24s transitions in the Si sequence (K VI– Xe XLI) by using the relativistic quantum defect orbital (RQDO) method and the MCDF approach.

As the data for Rb XXIV are scarce, in this paper we present data on the radiative transition properties for Si-like Rb obtained by using a fully relativistic multiconfiguration Dirac– Fock approach which seems to be one of most reliable methods among the various standard methods suitable for predicting atomic data for transitions in highly charged or heavy atoms. In the present work, we calculate level compositions, energy levels, lifetimes for the lowest 97 levels of Rb XXIV, which belong to 3s23p2, 3s23p3d, 3s3p3, 3p4, 3s3p23d, and 3s23d2 configurations. Wavelengths, transition probabilities and oscillator strengths are calculated for E1, M1, E2, and M2 transitions. The atomic data we provide in this paper have not been reported before and may be useful in plasma diagnostics and various other fields. A comparison has been made wherever possible, and good agreement was achieved. To achieve the accuracy of our results, calculations have also been performed with the flexible atomic code (FAC). We have also provided a detailed comparison of our theoretical calculations with the data available from the NIST (National Institute of Standards and Technology)[54] database. An outline of the computational method is presented in Section 2 and results are discussed in Sections 3, 4, and 5.

2. Theoretical method

To calculate atomic data, we use the MCDF method originally developed by Grant et al.[55] and revised by Norrington[56] which has successfully been used earlier by ourselves and others.[57– 63] The relativistic effects and QED effects must be considered in the highly ionized atoms as the velocity of electrons in these cases is fast and the nuclear potential energy is very strong. MCDF is a fully relativistic method based on the jj-coupling scheme. It also includes the relativistic corrections arising due to the Breit interaction and QED effects (Vacuum Polarization and Lamb Shift). In our calculations, the extended average level (EAL) option has been adopted, in which a weighted (proportional to 2j + 1) trace of the Hamiltonian matrix is minimized by producing a compromised set of orbitals. The results are evaluated with the Babushkin gauge, which in the relativistic limit corresponds to the length form of matrix elements.

In the MCDF method, [64] the relativistic atomic state function Ψ for a state | PJM⟩ is obtained as linear combinations of symmetry adapted configuration state functions (CSFs).

where nc is the number of CSFs; γ i denotes the appropriate labeling of the configuration state function such as orbital occupancy, coupling scheme, etc.; J and M are the angular quantum numbers; P denotes the parity. The CSFs are obtained from products of one-electron Dirac orbitals. Configuration mixing coefficients Ci(α ) can be obtained through the diagonalization of Dirac Coulomb Hamiltonian

where VN denotes the electron– nucleus Coulomb interaction, α and β are the 4× 4 Dirac matrices, and c is the speed of light in atomic units. The configuration state functions Φ , which are eigen functions of J2, JZ, and P are built as linear combinations of Slater determinants. A Slater determinant, in the Dirac– Fock model, is a product of one-electron Dirac orbitals.

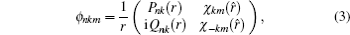
where n is the principal quantum number, k and m are the relativistic angular quantum number and its z component respectively, k = ± (j + 1/2) for l = j ± 1/2 with l and j being the orbital and total angular momenta of the electron, Pnk(r) and Qnk(r) denote the large and small component one-electron radial wavefunctions and are obtained as a self-consistent field solution of one-electron Dirac– Fock equation, [64] and χ km (r̂ ) are the spinor spherical harmonics in the ls j coupling scheme and expressed as

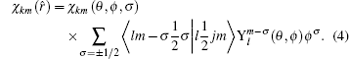
The energy of the N-electron system is given as

where the Hamiltonian matrix HDC is expressed as

For the energy to be stationary with respect to variations in mixing co-efficients Ci (α ) subject to orthonormality condition (Ci (α ))+ Cj (α ) = δ ij, the following equation holds

where I is the nc × nc unit matrix. The predicted atomic energy level Eα thus can now be taken to be eigenvalues of HDC.

Since no detailed results are available, to assess the accuracy of our results and to make comparisons, analogous calculations are performed by using the Flexible Atomic Code (FAC) of Gu.[65] It is also a fully relativistic configuration interaction program and provides the results for energy levels and transition probability values comparable to MCDF. In this case, the single electron-orbital radial wavefunctions are determined by using a self-consistent field method based on the Dirac formulation. The atomic state wavefunctions and energy levels are obtained by diagonalizing the Dirac– Coulomb Hamiltonian. There are no major discrepancies reported in the energy level and radiative rates results determined by the two codes.

3. Energy levels

In Table 1, we list our fine structure levels relative to the ground level for Rb XXIV using MCDF wavefunctions. Relativistic multiconfiguration Dirac– Fock (MCDF) self-consistent field (SCF) calculations are employed in calculating the transition energies and transition rates. MCDF SCF is effective in treating nondynamic correlation. As E2 transition rates depend on the fifth power of transition energy, the accurate calculations of transition energies are essential. MCDF involves relativistic, Dirac– Coulomb and Breit correlation energies and Lamb shift corrections in transition energy calculations, therefore it can provide accurate transition energies and transition rates among multiplet states of atoms for a wide range of ionizations. To achieve high accuracy with this method, various important configurations are used in our calculations. As found by various authors, [66, 67] for the ground state configuration 3s23p2, the largest interaction is from the highly excited 3p4 configuration. Also, the excited 3s23p4s configuration is found to interact strongly with 3s3p3 configuration states.[68] As reported by Bié mont, [15, 16] the perturbation between 3s3p3 and 3s23p3d is quite important. Therefore, all these configurations have been included in our MCDF calculations. The calculations involving one electron excitations are excluded by us due to their negligible contributions to the calculating of energy levels and oscillator strengths.

Table 1. Dirac– Coulomb (DC), Breit and Quantum Electrodynamics (QED) contributions to the MCDF energy (in Rydberg) for the lowest 97 levels as a function of the orbital set. The sum total is compared with FAC and other available results. All energies are relative to the ground state.

For reliable calculations and to form a reasonable correlation model, calculations are performed by taking two different sets of configurations. In the first set of calculations, we use 6 configurations (1s22s22p6) 3s23p2, 3s23p3d, 3s3p3, 3p4, 3s3p23d, and 3s23d2 referred to as MCDF1, which are listed in Table 1. For convergence, we perform another set of similar calculations, including some additional configurations namely 3s3p3d2, 3s3d3, 3p3d3, 3p23d2, 3p33d, 3d4, 3s23p4s, 3s23p4p, 3s23p4d, 3s23p4f, 3s3p24s, 3s3p24p, 3s3p24d, and 3s3p24f referred to as MCDF2. As the results are found to be better for MCDF2 with stronger configuration interaction (CI) included in the calculations, we use MCDF2 for all our calculations. In MCDF2, we include CI among 20 configurations, keeping [1s22s22p6] frozen, namely 3s23p2, 3s3p3, 3p4, 3s23p3d, 3s23d2, 3s3p23d, 3s3p3d2, 3s3d3, 3p3d3, 3p23d2, 3p33d, 3d4, 3s23p4s, 3s23p4p, 3s23p4d, 3s23p4f, 3s3p24s, 3s3p24p, 3s3p24d, and 3s3p24f which generate 730 energy levels. Among these levels, we consider the lowest 97 fine-structure levels belonging to 3s23p2, 3s23p3d, 3s3p3, 3p4, 3s3p23d, and 3s23d2 configurations for our calculations. We perform similar calculations by using FAC which includes 3* 4, 3s23p 4* 1, 3s3p2 4* 1, 3s3d2 4* 1, 3s23d 4* 1, 3p3 4* 1, and 3d3 4* 1, which generate 4363 levels.

In Table 1, we list our calculated excitation energies of the fine structure levels obtained from the MCDF method with and without including Breit and QED effects for MCDF2. Before we discuss our results further, we note that Huang[20] calculated the energy levels for 27 low lying levels of Rb XXIV. However, these results are unreliable as can be seen from Table 1. Therefore, we do not discuss these results further. We find that our Breit and QED corrected energies are lower than the corresponding coulomb energies by up to ∼ 0.08 Ryd. Our level energies without the Breit and QED effects are higher than the NIST values by ∼ 0.16 Ryd. The energies are lowered by a maximum value of 0.08 Ryd with including the Breit and QED effects, which shows the importance of including higher relativistic effects for heavy ions. Further, it is seen that QED corrections are comparable to or greater than those with including the Breit effect for levels where single and double electron excitations from 3s to 3p and 3d orbitals occur, such as for levels 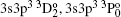, and whereas QED corrections are smaller for levels formed due to excitations from 3p to a higher orbital such as 3s23d2  3F2, 3. Energies obtained with including the Breit and QED effects are lower than the NIST values by 1.2%. Unfortunately, data available on NIST are limited to only a few levels. One can see that the energy values obtained from the FAC code agree well with our MCDF2 results within 0.54%. The level ordering is found to be generally the same except at a few places between the two calculations. Differences between the calculations occur due to the different ways in which the central potentials for radial orbitals and recoupling schemes of angular parts are calculated. Considering the results of NIST as a standard reference for comparison we find that the agreement of our MCDF2 energy levels with NIST results is within 1.2% which shows the reliability of our levels.

We also list the mixing coefficients for these 97 levels in Table 2. Under the column LSJ coupling the first number of each entry denotes the leading percentage of the level corresponding to the level number in the first column. The next leading percentage is in the form P(Q) where the next leading percentage is P% of Q level number in the first column. We note that some of the levels are easily identifiable such as due to clear dominance. For many levels, the mixing of eigenvectors from different levels is very strong. For example, is strongly coupled with and with their mixing being 27%, 22%, and 20% respectively. Further, we notice that due to the strong mixing among the levels , and 3p4  1D2, these levels can be interchanged. Sometimes the same eigenvector dominates over several levels and the identification of such levels is ambiguous as levels Nos. 54 and 65 are unidentifiable in our calculations. There remains scope for re-designation as the identification is not unique for a few levels. The corresponding jj designations for the levels have also been provided under the column “ JJ coupling” as the LSJ coupling is not found to be accurate for highly mixed levels. Under this column, the first number represents the leading percentage of the level and p− , p, d− , d denote p1/2, p3/2, d3/2, and d5/2 respectively.

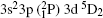
Table 2. Level Nos., Wave-function compositions and lifetimes of the first 97 fine structure levels of Rb XXIV using MCDF2.
4. Radiative rates

For a transition i → j, the absorption oscillator strength fij (dimensionless), and radiative rate Aji (in s− 1) are related by

where m and e denote the electron mass and charge respectively, c is the velocity of light, λ ji represents the transition wavelength in Å , and wi and wj are the statistical weights of the lower i and upper j levels respectively. The line strength Sij and the oscillator strength fij obey the following relations:

(i) for electric dipole transitions (E1)

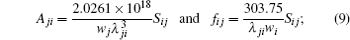
(ii) for the magnetic dipole transitions (M1)

(iii) for electric quadrupole transitions (E2)

(iv) for the magnetic quadrupole transitions (M2)

The wavelengths (λ in Å ), radiative rates (Aji in s− 1), oscillator strengths (fij dimensionless), line strengths (Sij in atomic unit “ a.u.” ) determined from the ground level for transitions among all the 97 levels considered in this paper by using MCDF wavefunctions are given in Tables 3 and 4. Some of the strong lines belonging to n = 3→ 3 transition arrays of the silicon sequence which appears in laboratory plasma and in astrophysical sources are important for solar identifications. An intercombination, or spin-forbidden, line signals the breakdown of the spin conservation rule for transitions, due to the spin– orbit effect like spin-dependent interactions. In astrophysical precision spectroscopy and diagnostics of laboratory plasma, many lines are observed due to spin-forbidden transitions. These are useful in understanding density fluctuations and other elementary processes occurring in interstellar and laboratory plasmas. In the present work, we list the transition probabilities, oscillator strengths of such transitions like , 3s23p2  3P0– 3s23p3d 5F2, 5P2, 5D2. As spin-forbidden transitions arise due to small mixing of states, such data can also be used for testing atomic theory.

Table 3. Transition data for E1 and E2 transitions for Si-like Rb from 3s23p2  3Po: levels and J for lower level i, upper level k, wavelength λ (in Å ), transition rate Aji (length form), oscillator strength fij (length form), line strength Sij (in atomic unit a.u.) (length form),
Table 4. Transition data for M1 and M2 transitions for Si-like Rb from 3s23p2  3Po: levels and J for lower level i, upper level k, wavelength λ (in Å ), transition rate Aji (length form), oscillator strength fij (length form), line strength, Sij (in unit a.u.) (length form).

We adopt the length gauge in our calculations, as length results are expected to be more accurate than the velocity results. The velocity results are much more sensitive to the choice of configurations while the length form for transitions is stabler. The value of the ratio of vel./len. form indicates the calculation precision as it indicates the accuracy of f- or A-values. As seen from Table 3, the vel./len ratio in our case is generally within 10% of unity for most of the strong transitions (f ≥ 0.1) listed in Table 3. For some strong transitions such as , , etc., the ratio is exactly unity. For weaker transitions (f ∼ 10− 5 or less), such as 3s23p2  3P0– 3s23p2  3P2, 3s23p2  3P0– 3s23p2  1D2, 3s23p2  3P0– 3s3p23d 5F2, and 3s23p2  3P0– 3s23d2  3P2, the ratio is higher. As the discrepancy between both length and velocity forms sometimes may be large for weaker transitions, it does not affect the overall accuracy of our calculations because weaker transitions are found to be sensitive to the cancellation effects among mixing coefficients and are not very important. Most of the spectral lines are found to be obtained in EUV (100– 1200 Å ) and x-ray (< 100 Å ) regions. Further we notice a sudden decrease in wavelength for transition from 474.2 Å to 83.32 Å in Table 3 when the upper level changes from 3s23p2  1D2 to 3p4  3P2 and in Table 4 for levels from upper level 3s23p2  3P1 to 3s3p2 from 1266 Å to 81.97 Å which may be due to the increase in the force of repulsion between core and valence electrons through exciting an electron from 3p to 3d orbital, thereby increasing the transition energy.

Table 5. Comparison of computed wavelengths (in Å ) with observed wavelengths from NIST and other theories for transitions from 3s23p2  3P0, 1, 2 to selected upper levels.

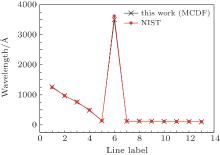
In Table 5, we compare our calculated wavelengths of Rb XXIV with those published by Huang[20] and those compiled by NIST. We observe that our results are in reasonable agreement with those present in the literature. The maximum disagreement between our calculated MCDF transition wavelengths and the NIST results is 3.37% while 11.5% with those of Huang.[20] Also, the mean ratio λ Thiswork/λ exp. is found to be 0.9897, which indicates the accuracy of our results. The difference between our results and Huang’ s[20] are mainly because of the different amounts of CI included. Our results are expected to be more reliable as we have included larger CI for our calculations. We plot our wavelengths and NIST values in Fig. 1. The horizontal axis represents ’ Line Label’ corresponding to transition labels as indicated in the first column of Table 5.

Fig. 1. MCDF (cross) and observed NIST (circle) wavelengths versus transition.

From Table 6, we find that our A-values are in reasonable agreement with NIST values except for transitions 3s23p2 and . A reassessment of transition probability data for these transitions for Rb XXIV on the NIST website is desirable. Our results are comparable to those of Huang for some transitions while for some other transitions there is a huge discrepancy. Our A-values from the MCDF and FAC agree well with each other, showing that the CI included in the calculations is sufficient enough to produce accurate radiative rates. Table 7 shows a comparison of our f-values from ground level 3s23p2  3Po with the results presented by Huang[20] using MCDF and by Charro et al.[27] using RQDO. Similarly, Table 8 shows a comparison of line strength results with the results given by Huang, [20] the only available results in the literature.

Table 6. Comparison of computed transition probabilities Aji/s− 1 with those from NIST and other theories for transition from 3s23p2  3P0, 1, 2 to selected upper levels.
Table 7. Comparison of computed oscillator strengths fij with those from NIST and different theories for transition from 3s23p2  3P0 to selected upper levels.
Table 8. Comparison of computed line strengths Sij (in unit a.u.) with those from NIST and different theories for transition from 3s23p2  3P0 to selected upper levels.
5. Lifetimes

Table 1 includes the values of radiative lifetimes for all 97 levels in the length gauge from our calculations, and these values are obtained from our radiative transition probabilities Aji which are obtained from the following expression:

where the summation over i refers to the sum of all accessible final states and the values of Δ E = Ej − Ei. Lifetime calculations include A-values from all types of transitions, i.e., E1, E2, M1, and M2. Lifetimes for the levels 3s3p3  3P1, 3s3p3  3P2, 3s3p3  1D2, 3s3p3  1S0, 3s3p3  5S0, and are larger than those for other levels. As equation (13) provides a means of comparing theory (transition probability) with experiment (lifetimes), our results will be useful for experimentalists in future to make comparison between experimental results and theoretical values and also to check the accuracy of calculations.

6. Conclusions

In this work, fine structure energy levels, oscillator strengths, line strengths and transition probabilities for transitions between the levels belonging to 3s23p2, 3s23p3d, 3s3p3, 3p4, 3s3p23d, and 3s23d2 of Rb XXIV are obtained by using MCDF wavefunctions. We perform two independent calculations by using MCDF and FAC to compare energy levels and transition probabilities. Comparisons are performed between these two sets of energy levels, as well as with other available results, showing that they are in good agreement with each other. Though all the care is taken to identify the levels according to the strengths of eigenvectors, still there always lies a possibility of their redesignation. We also conduct a comparison for other parameters, especially for transition wavelengths. In general, the accuracies of listed wavelength values are assessed to be within 3.37%. Further, the lifetimes of all 97 levels are also reported.

We believe that our atomic data have been the most extensive and definitive to date and will be useful in controlled thermonuclear fusion research, astrophysical applications and in technical plasma modeling.

Reference
1 Chand ra x-ray Observatory. Available at http://chandra.harvard.edu/ [Cited within:1]
2 The Solar and Heliospheric Observatory. Available at http://sohowww.nascom.nasa.gov/ [Cited within:1]
3 Behringer K 2000in Atomic and Molecular Data and their ApplicationsBerrington K A and Bell K L New York AIP 142 [Cited within:1]
4 Liedahl D A, Beiersdorfer P, Brown G V, Utter S B, Khan S M, Gu M F and Savin D W 1998Laboratory Space Science WorkshopApril 1–3, 1998 Washington, NASA, USA 85 [Cited within:1]
5 Edlén B 1983 Phys. Scr. T 8 5 [Cited within:1]
6 Träbert E, Heckmann P H, Hutton R and Martinson I 1988 J. Opt. Soc. Am. B 5 2173 [Cited within:1]
7 Ellis D G, Martinson I and Träbert E 1900 Comm. At. Mol. Phys. 22 241 [Cited within:1]
8 Seaton M J 1987 J. Phys. B: At. Mol. Opt. Phys. 20 6363 DOI:10.1088/0022-3700/20/23/026 [Cited within:1]
9 Widing K G, Sand lin G D and Cowan R D 1971 Astrophys. J. 169 405 DOI:10.1086/151151 [Cited within:1]
10 Malinovsky M and Heroux L 1973 Astrophys. J. 181 1009 DOI:10.1086/152108 [Cited within:1]
11 Behring W E, Cohen L, Doschek G A and Feldman U 1976 Astrophys. J. 203 521 DOI:10.1086/154107 [Cited within:1]
12 Fawcett B C 1971 J. Phys. B: At. Mol. Opt. Phys. 4 1577 DOI:10.1088/0022-3700/4/11/021 [Cited within:1]
13 McWhirter R W R and Summers H P 1984 Appl. At. Coll. Ph. 2 51 [Cited within:1]
14 Brage T, Judge P G and Brekke P 1996 Astrophys. J. 464 1030 DOI:10.1086/177390 [Cited within:1]
15 Biémont E 1986 J. Opt. Soc. Am. B 3 163 DOI:10.1364/JOSAB.3.000163 [Cited within:2]
16 Biémont E 1986 Phys. Scr. 33 324 DOI:10.1088/0031-8949/33/4/007 [Cited within:1]
17 Bromage G E 1980 Astron. Astrophys. 41 79 [Cited within:1]
18 Bromage G E, Cowan R D and Fawcett B C 1978 Mon. Not. R. Astron. Soc. 183 19 DOI:10.1093/mnras/183.1.19 [Cited within:1]
19 Cowan R D 1981in The Theory of Atomic Structure and Spectra Berkeley, CA University of California Press [Cited within:1]
20 Huang K N 1985 At. Data Nucl. Data Tables 32 503 DOI:10.1016/0092-640X(85)90022-1 [Cited within:7]
21 Fawcett B C 1987 At. Data Nucl. Data Tables 36 129 DOI:10.1016/0092-640X(87)90018-0 [Cited within:1]
22 Hibbert A 1988 Phys. Scr. 38 87 [Cited within:1]
23 Nahar S N 1993 Phys. Scr. 48 297 DOI:10.1088/0031-8949/48/3/008 [Cited within:1]
24 Kohstall C, Fritzsche S, Fricke B and Sepp W D 1998 At. Data Nucl. Data Tables 70 63 DOI:10.1006/adnd.1998.0786 [Cited within:1]
25 Nahar S N 1993 Phys. Scr. 48 297 DOI:10.1088/0031-8949/48/3/008 [Cited within:1]
26 Nahar S N 1999 At. Data Nucl. Data Tables 72 129 DOI:10.1006/adnd.1999.0811 [Cited within:1]
27 Charro E, Martin I and Lavin C 1997 Astron. Astrophys. Suppl. Ser. 124 397 DOI:10.1051/aas:1997200 [Cited within:2]
28 Saha B, Das A K and Mukherjee P K 2001 Eur. Phys. J. D 14 33 DOI:10.1007/s100530170231 [Cited within:1]
29 Saha B, Mukherjee T K, Das A K and Mukherjee P K 2003 Int. J. Quantum Chem. 91 626 DOI:10.1002/(ISSN)1097-461X [Cited within:1]
30 Land i E and Bhatia A K 2003 Astrophys. J. 589 1075 DOI:10.1086/apj.2003.589.issue-2 [Cited within:1]
31 Tayal V and Gupta G P 2007 Phys. Scr. 75 331 DOI:10.1088/0031-8949/75/3/019 [Cited within:1]
32 Froese Fisher C, Tachiev G and Irimia A 2006 At. Data Nucl. Data Tables 92 607 DOI:10.1016/j.adt.2006.03.001 [Cited within:1]
33 Ishikawa Y and Vilkas M J 2001 Phys. Rev. A 63 042506 DOI:10.1103/PhysRevA.63.042506 [Cited within:1]
34 Ishikawa Y and Vilkas M J 2003 Phys. Rev. A 68 012503 DOI:10.1103/PhysRevA.68.012503 [Cited within:1]
35 Tayal V and Gupta G P 2007 Phys. Scr. 75 331 DOI:10.1088/0031-8949/75/3/019 [Cited within:1]
36 Gupta G P and Msezane A Z 2011 Phys. Scr. 83 055301 DOI:10.1088/0031-8949/83/05/055301 [Cited within:1]
37 Gupta G P and Msezane A Z 2012 Phys. Scr. 86 015303 DOI:10.1088/0031-8949/86/01/015303 [Cited within:1]
38 Träbert E, Pinnington E H, Kernahan J A, Doerfert J, Granzow J, Heckmann P H and Hutton H J 1996 J. Phys. B: At. Mol. Opt. Phys. 29 2647 DOI:10.1088/0953-4075/29/13/005 [Cited within:1]
39 Fawcett B C and Hayes R W 1972 J. Phys. B: At. Mol. Opt. Phys. 5 366 DOI:10.1088/0022-3700/5/2/032 [Cited within:1]
40 Kastner S O, Swartz M, Bhatia A K and Lapides J 1978 J. Opt. Soc. Am. 68 1558 DOI:10.1364/JOSA.68.001558 [Cited within:1]
41 Träbert E, Grieser M, Krantz C, Repnow R, Wolf A, Diaz F J, Ishikawa Y and Santana J A 2012 J. Phys. B: At. Mol. Opt. Phys. 45 215003 DOI:10.1088/0953-4075/45/21/215003 [Cited within:1]
42 Khan M A 1978 Opt. Commun. 27 242 DOI:10.1016/0030-4018(78)90373-5 [Cited within:1]
43 Sugar J, Kaufmann V and Rowan W L 1990 J. Opt. Soc. Am. B 7 152 [Cited within:1]
44 Wyart J FTFR Group 1988 Phys. Scr. 37 66 DOI:10.1088/0031-8949/37/1/010 [Cited within:1]
45 Jupén C, Martinson I and Denne-Hinnov B 1991 Phys. Scr. 44 562 DOI:10.1088/0031-8949/44/6/009 [Cited within:1]
46 Träbert E 1993 Phys. Scr. 48 699 DOI:10.1088/0031-8949/48/6/009 [Cited within:1]
47 Träbert E 1986 Z. Phys. D 2 213 DOI:10.1007/BF01429076 [Cited within:1]
48 Träbert E 1987 Z. Phys. D 5 125 DOI:10.1007/BF01436886 [Cited within:1]
49 Rodrigues G C, Indelicato P, Santos J P, Patté P and Parente F 2004 At. Data Nucl. Data Tables 86 117 DOI:10.1016/j.adt.2003.11.005 [Cited within:1]
50 Carlson Thomas A, Nestor C W, Neil Wasserman J R and McDowell J D 1970 Atomic Data 2 63 DOI:10.1016/S0092-640X(70)80005-5 [Cited within:1]
51 Sugar J and Kaufmann V 1984 J. Opt. Soc. Am. B 1 218 DOI:10.1364/JOSAB.1.000218 [Cited within:1]
52 Biémont E, Frémat Y and Quinet P 1999 At. Data Nucl. Data Tables 71 117 DOI:10.1006/adnd.1998.0803 [Cited within:1]
53 Aguiar Julio C and Di Rocco Héctor O 2014 J. Quantum Spectrosc. Radiat. Transfer 49 1 [Cited within:1]
54 Kramida A, Ralchenko Yu and Reader JNIST ASD Team 2014 NIST Atomic Spectra DatabaseVersion 5. 2, Online available at: http://physics.nist.gov/asd [Cited within:1]
55 Grant I P, Mckenzie B J, Norrington P H, Mayers D F and Pyper N C 1980 Comput. Phys. Commun. 21 207 DOI:10.1016/0010-4655(80)90041-7 [Cited within:1]
56 Norrington P H 2009http://www.am.qub.ac.uk/DARC/ [Cited within:1]
57 Quinet P 2012 J. Phys. B: At. Mol. Opt. Phys. 45 025003 DOI:10.1088/0953-4075/45/2/025003 [Cited within:1]
58 Gu M F 2008 Can. J. Phys. 86 675 [Cited within:1]
59 Singh A K, Aggarwal S and Mohan M 2013 Phys. Scr. 88 035301 DOI:10.1088/0031-8949/88/03/035301 [Cited within:1]
60 Aggarwal S, Singh J and Mohan M 2013 At. Data Nucl. Data Tables 99 704 DOI:10.1016/j.adt.2013.02.001 [Cited within:1]
61 Aggarwal K M, Keenan F P and Msezane A Z 2003 At. Data Nucl. Data Tables 85 453 DOI:10.1016/j.adt.2003.09.001 [Cited within:1]
62 Goyal A, Khatri I, Aggarwal S, Singh A K and Mohan M 2013 Can. J. Phys. 91 394 DOI:10.1139/cjp-2013-0013 [Cited within:1]
63 Aggarwal S, Jha A K S, Khatri I, Singh N and Mohan M 2015 Chin. Phys. B 24 053201 DOI:10.1088/1674-1056/24/5/053201 [Cited within:1]
64 Grant I P 1988in Relativistic Effects in Atoms and MoleculesWilson S ( Methods in Computational Chemistry), Vol. 2 New York Plenum Press 1 71 [Cited within:2]
65 Gu M F 2003 Astrophys. J. 582 1241 DOI:10.1086/apj.2003.582.issue-2 [Cited within:1]
66 Flambaum V V and Sushkow O P 1978 J. Quantum. Spectros. Radiat. Transfer 20 569 DOI:10.1016/0022-4073(78)90028-6 [Cited within:1]
67 Biémont E and Hansen J E 1986 Phys. Scr. 33 117 DOI:10.1088/0031-8949/33/2/006 [Cited within:1]
68 Dembczynski J and Rebel H 1984 Physica 125C 341 [Cited within:1]