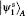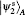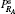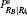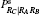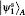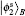Over the past decades, the application of quantum mechanics in the field of computer science and information theory has motivated an emerging research area, quantum computation and quantum information.^[1] Encoding information in quantum states provides a totally new method for information processing beyond the capabilities of its classical counterparts. Transferring a quantum state faithfully and securely between remote communicating peers is of greatest significance. One of the most remarkable protocols for states transmission is quantum teleportation, put forward by Bennett et al.^[2] in 1993, allowing the teleportation of an unknown quantum state via an Einstein– Podolsky– Rosen (EPR) pair as the quantum channel with the aid of Bell measurement and two bits of classical communication. Later, a new protocol referred to as remote state preparation (RSP)^{[3– 5]} was introduced, in which a known state can be remotely prepared using the same quantum channel as in quantum teleportation but with lower classical communication cost. However, in RSP full knowledge of the to-be-prepared state (generally called the target state) is disclosed to the sender. To overcome this drawback, joint remote state preparation (JRSP)^{[6, 7]} was proposed. It mainly deals with the scenario that the complete set of parameters identifying the target state is shared by two or more senders located in different places who tend to remotely prepare the target state at the receiver’ s site with mutual collaboration.

Due to its significant advantages in quantum states transmission, JRSP has been extensively investigated both theoretically^{[8– 14]} and experimentally.^{[15, 16]} Nevertheless, most of them are accomplished only with success probabilities of less than 100%, that is, they are probabilistic. In recent years, Xiao, ^[17] An, ^[18] Bich, ^[19] Xia, ^[20] Zhan, ^[21] and Wang^[22] independently put forward a series of deterministic JRSP protocols. As a matter of fact, the above-mentioned deterministic JRSP protocols are realized via maximally entangled quantum channels. Generally speaking, due to the unavoidable interaction between the quantum channel and its surrounding environment, the maximally entangled states may readily evolve into the partially entangled states.^{[23– 25]} Taking this into consideration, very recently, Jiang^[26] presented a scheme for deterministic JRSP of general multi-qubit states via a partially entangled Greenberger– Horne– Zeilinger (GHZ)-type channel. However, in their scheme, the unit success probability is generally ensured by recursive channel modulations.

In this paper, we are focusing our attention on the deterministic JRSP of arbitrary single- and two-qubit states with the above-mentioned limitations removed. Considering the technological challenges to prepare and maintain maximal entanglement in real-world implementations, we construct a set of ingenious four-particle partially entangled states to serve as the quantum channels. To accomplish the JRSP tasks, participants cooperate with each other and perform projective measurements on their own particles, combined with the feed-forward technique.^{[14, 17]} Based on their measurement results, the receiver can reestablish the target state by means of appropriate local unitary operations with unit success probability, which is demonstrated by detailed analysis.

The rest of this paper is organized as follows. In Section 2, an ingenious partially entangled quantum channel is constructed. In Section 3, a scheme is proposed for implementing deterministic JRSP of an arbitrary single-qubit state and the corresponding quantum logic circuit is designed, then we extend it to a scheme involving arbitrary two-qubit states in Section 4. Finally, some conclusions are drawn in Section 5.

The four-particle partially entangled state that we characterize throughout this paper can be represented as

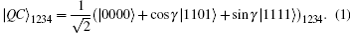
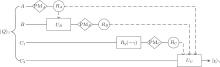
To obtain this state, we construct a quantum circuit by using the compositions of Hadamard gates, control-NOT (CNOT) gates and rotation gates, as shown in Fig. 1. H is the Hadamard operation^[1]

With the dot “ • ” denoting the control qubit, the CNOT gate takes the form of the following 4 × 4 matrix:^[1]

Moreover, the rotation gate R_y(γ ) can be expressed as^[1]

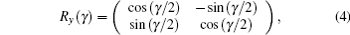
where γ indicates the tangle of rotation around the y-axis.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Quantum circuit to obtain the partially entangled quantum channel | QC⟩ 1234.

The input of the circuit is a separable state | 0000⟩ ₁₂₃₄, due to the Hadamard operation and the first three CNOTs, a four-qubit GHZ state is obtained

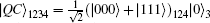
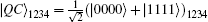
After the subsequent R_y (− γ ), CNOT, and R_y (γ ) operations, | GHZ⟩ _four can be transformed to the desired four-particle partially entangled state | QC⟩ ₁₂₃₄, expressed as Eq. (1). This state is characterized by a single parameter γ , whose value is known to the receiver alone. Based on Eq. (1), when γ = 0, , this is a separable state with respect to the particles 1, 2, 4, and 3, while if γ = π /2, then , a maximally entangled state. We are here interested in 0 < γ < π /2 for which the state | QC⟩ ₁₂₃₄ is partially entangled with the entanglement degree C_{1, 2, 4| 3} = | sin γ | quantified by the concurrence.^[27]

In this section, we detail our scheme for deterministic JRSP of an arbitrary single-qubit state. Suppose that two independent senders, Alice and Bob, located at two spatially separated places, intend to help a remote receiver Charlie prepare an arbitrary single-qubit state taking the general form

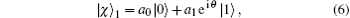
where | 0⟩ and | 1⟩ are two eigenstates of a single-qubit, the real coefficients a₀, a₁ ≥ 0, and θ ∈ [0, 2π ] with the normalization condition 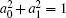. Consistent with existing JRSP schemes, ^{[17, 18, 26]} the information of the target state is shared by the senders Alice and Bob. In detail, the amplitude information {a₀, a₁} is completely known to Alice, Bob knows the phase θ . Therefore, only if both senders cooperate with each other, can they have the complete knowledge of the target state | χ ⟩ ₁. The receiver Charlie knows nothing about | χ ⟩ ₁.

To achieve the task of JRSP, Alice, Bob, and Charlie initially share the following partially entangled quantum channel:

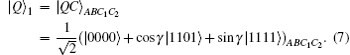
Subscripts indicate that particle A belongs to Alice, Bob is in possession of particle B, and Charlie owns particles C₁ and C₂. Generally, Charlie is responsible for the preparation of the quantum channel | QC⟩ _ABC1C2, subsequently he will distribute particles A and B to Alice and Bob, respectively, with particles C₁ and C₂ reserved in his local site.

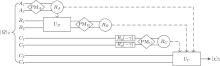
In order to help Charlie prepare the target state | χ ⟩ ₁, as shown in Fig. 2, firstly, Alice performs a projective measurement on her particle A (PM_A). Based on her knowledge of the target state, Alice chooses a set of measurement basis:

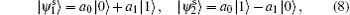
where the superscript “ s” indicates the scenario involving single-qubit states.

According to the measurement postulate of quantum mechanics, the shared quantum channel | Q⟩ ₁ can be rewritten in terms of Alice’ s measurement basis as

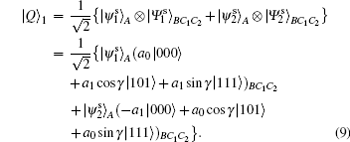
From Eq. (9) it is easily verified that Alice’ s PM_A will project the joint state of particles B, C₁, C₂ onto one of the two possible states 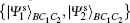with equal probability of After her projective measurement PM_A, Alice broadcasts some classical information about her measurement result to Bob and Charlie. Conditioned on Alice’ s PM_A result, Bob carries out suitable local unitary operation (U_B) on his particle B, as listed in Table 1.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Schematic quantum circuit for deterministic JRSP of an arbitrary single-qubit state via the four-particle partially entangled channel. Here, PMA, PMB, and PMC indicate Alice’ s, Bob’ s, and Charlie’ s projective measurements on their own particles with measurement results denoted by RA, RB, and RC, respectively.

Table 1.

Table 1.

Table 1. Corresponding relations between Alice’ s PMA result and Bob’ s unitary operation. Here I is the identity operator and σ x is Pauli-X operator. Alice’ s PMA result (RA) Bob’ s unitary operation (UB) I σ x

Table 1. Corresponding relations between Alice’ s PMA result and Bob’ s unitary operation. Here I is the identity operator and σ x is Pauli-X operator.

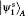
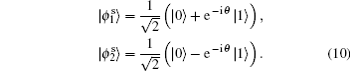
Without loss of generality, here we consider the case that the result of Alice’ s PM_A is . According to Table 1, Bob performs identity operation I on his particle B. Subsequently, he will implement the projective measurement on particle B (PM_B) under the following basis:

Above operations can be expressed analytically as follows:

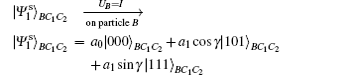
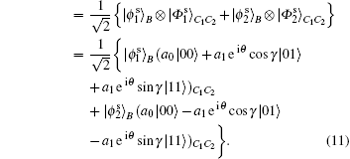
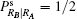
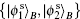
From Eq. (11) it is transparent that after Bob’ s projective measurement PM_B, with an equal probability , Bob will obtain one of the two possible states which he needs to inform Charlie by virtue of classical communication media. Upon receiving Bob’ s message, Charlie applies R_y (− γ ) on his particle C₁, followed by a projective measurement on the same particle (PM_C) with the computational basis {| 0⟩ , | 1⟩ }. Finally, taking into account Alice’ s, Bob’ s and his own measurement results, Charlie will carry out an appropriate recovery operation (U_C) on his own particles C₂ to reestablish the target state | χ ⟩ ₁. Various situations are listed out in Table 2.

Table 2.

Table 2.

Table 2. Charlie’ s recovery operator UC conditioned on Alice’ s RA, Bob’ s RB, and Charlie’ s RC, where I is the identity operator and σ x, iσ y, and σ z are Pauli matrices. The probabilities (or conditional probabilities) associated with various measurement results are also listed. Alice’ s RA Bob’ s RB Charlie’ s RC UC 1/2 1/2 | 0⟩ C1 cos2(γ /2) I | 1⟩ C1 sin2(γ /2) σ z 1/2 | 0⟩ C1 cos2(γ /2) σ z | 1⟩ C1 sin2(γ /2) I 1/2 1/2 | 0⟩ C1 cos2(γ /2) iσ y | 1⟩ C1 sin2(γ /2) σ x 1/2 | 0⟩ C1 cos2(γ /2) σ x | 1⟩ C1 sin2(γ /2) iσ y

Table 2. Charlie’ s recovery operator UC conditioned on Alice’ s RA, Bob’ s RB, and Charlie’ s RC, where I is the identity operator and σ x, iσ y, and σ z are Pauli matrices. The probabilities (or conditional probabilities) associated with various measurement results are also listed.

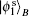
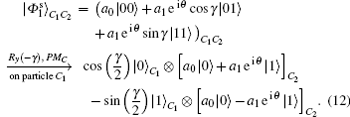
As an example, we might as well consider the situation that the result of Bob’ s PM_B is . Based on Eq. (11), the state of particles C₁ and C₂ evolves as

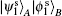
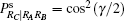
From Eq. (12), it is apparent that after Charlie’ s PM_C, the state of particle C₂ is perfectly correlated to the target state | χ ⟩ ₁. In our discussion here, Alice’ s PM_A and Bob’ s PM_B results are , if the result of Charlie’ s PM_C is | 0⟩ _C1 with the probability of , then U_C = I is required to perform on particle C₂, the target state | χ ⟩ ₁ can be readily recovered, as shown in Table 2.

As a supplement, when it comes to the other case corresponding to Alice’ s PM_A result , there will be a similar analysis process. In order for brevity, here we no longer depict it. According to Table 2, for all the possible measurement results of Alice, Bob, and Charlie, the receiver Charlie is always able to reconstruct the target state | χ ⟩ ₁ by performing appropriate unitary operation U_C on particle C₂. Thus, our JRSP scheme is deterministic. Mathematically, the total success probability reads

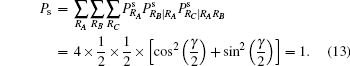
We now turn our attention to discuss the deterministic JRSP of an arbitrary two-qubit pure state. Following the basic idea in Section 3, suppose that two distantly separated senders, Alice and Bob, intend to help the receiver Charlie remotely prepare an arbitrary two-qubit state, which reads

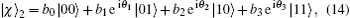
where the real coefficients b_i ≥ 0 (i = 0, 1, 2, 3) and θ _j ∈ [0, 2π ], (j = 1, 2, 3) with the normalization condition 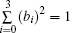. The target state | χ ⟩ ₂ is known partially to Alice and Bob. Concretely, the coefficients b_i (i = 0, 1, 2, 3) are known to Alice, while Bob has the knowledge of θ _j (j = 1, 2, 3). Therefore, neither one of the two senders alone can help the receiver Charlie, who has no idea of the target state at all, to reconstruct | χ ⟩ ₂ at his place.

To accomplish the task of JRSP, the senders Alice, Bob, and the receiver Charlie previously share the quantum channel consisting of two four-particle partially entangled states given by

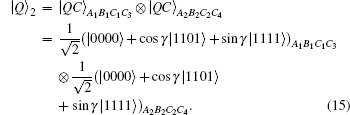
Among these eight particles, particles A₁ and A₂ belong to Alice, Bob is in possession of particles B₁ and B₂, and Charlie owns particles C₁, C₂ and C₃, C₄. Consistent with the basic idea in Section 3, Charlie is responsible for the preparation of the quantum channel | QC⟩ _A1B1C1C3 ⊗ | QC⟩ _A2B2C2C4, subsequently he will distribute particles A₁, A₂ to Alice, and B₁, B₂ to Bob, with particles C₁, C₂ and C₃, C₄ reserved by himself.

As is shown in Fig. 3, for the purpose of achieving the JRSP task, firstly, Alice carries out joint projective measurement on her particles A₁ and A₂ (PM_A) by choosing a set of complete orthonormal basis {| ψ ₁⟩ , | ψ ₂⟩ , | ψ ₃⟩ , | ψ ₄⟩ } conditioned on her knowledge of the target state | χ ⟩ ₂, which reads

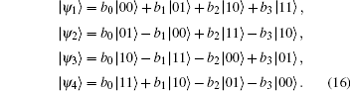
According to the measurement postulate of quantum mechanics, the whole quantum system consisting of eight particles can be expressed in terms of Alice’ s measurement basis as

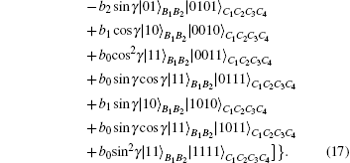
Alice’ s projective measurement PM_A will project the joint state of particles B₁, B₂, C₁, C₂, C₃, C₄ onto one of the four possible states {| Ψ ₁⟩ , | Ψ ₂⟩ , | Ψ ₃⟩ , | Ψ ₄⟩ }_B1B2C1C2C3C4 with an equal probability of P_RA = 1/4, as shown in Eq. (17). After her projective measurement, Alice broadcasts her result to Bob and Charlie. Conditioned on the received PM_A result, Bob selects suitable unitary operations (U_B) to perform on his particles B₁ and B₂. Various situations involving Alice’ s PM_A results and Bob’ s unitary operations are listed out in Table 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Schematic quantum circuit for deterministic JRSP of an arbitrary two-qubit state, in which PMA, PMB, and PMC indicate Alice’ s, Bob’ s, and Charlie’ s projective measurements on their own particles with measurement results denoted by RA, RB, and RC, respectively.

Table 3.

Table 3.

Table 3. Corresponding relations between Alice’ s PMA result and Bob’ s unitary operation. Alice’ s PMA result (RA) Bob’ s unitary operation(UB) | ψ 1⟩ A1A2 I⊗ I | ψ 2⟩ A1A2 I⊗ σ x | ψ 3⟩ A1A2 σ x⊗ I | ψ 4⟩ A1A2 σ x⊗ σ x

Table 3. Corresponding relations between Alice’ s PMA result and Bob’ s unitary operation.

Without loss of generality, here we consider the case that Alice’ s PM_A result is | ψ ₂⟩ _A1A2. At this point, Bob will carry out the unitary operation U_B = I ⊗ σ _x on his particles B₁ and B₂, and subsequently, on the same particles, he performs projective measurement (PM_B) with the following complete orthonormal basis:

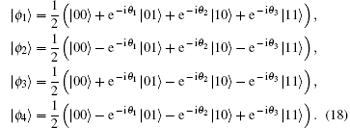
Above operations can be expressed analytically as follows,

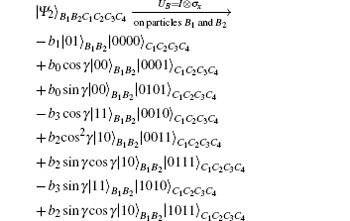
From Eq. (19) it is obvious that after the projective measurement PM_B, with an equal probability P_{RB| RA} = 1/4, Bob will obtain one of the possible states {| ϕ ₁⟩ , | ϕ ₂⟩ , | ϕ ₃⟩ , | ϕ ₄⟩ }_B1B2 which he needs to inform Charlie with the aid of classical communication. Upon receiving Bob’ s message, Charlie applies R_y (− γ ) ⊗ R_y (− γ ) on his particles C₁ and C₂, followed by a projective measurement on the same particles (PM_C) under the basis {| 00⟩ , | 01⟩ , | 10⟩ , | 11⟩ }. Finally, depending on Alice’ s, Bob’ s and his own measurement results, Charlie’ s job is simply to perform an appropriate unitary operation (U_C) on particles C₃ and C₄ to recover the target state | χ ⟩ ₂. Various situations are listed out in Table 4.

Table 4.

Table 4.

Table 4. Charlie’ s recovery unitary operator UC conditioned on Alice’ s RA, Bob’ s RB, and Charlie’ s RC, where I is the identity operator and σ x, iσ y, σ z are Pauli matrices. RA, RB, RC UC RA, RB, RC UC RA, RB, RC UC RA, RB, RC UC | ψ 1⟩ | ϕ 1⟩ | 00⟩ I⊗ I | ψ 2⟩ | ϕ 1⟩ | 00⟩ I⊗ iσ y | ψ 3⟩ | ϕ 1⟩ | 00⟩ iσ y⊗ σ z | ψ 4⟩ | ϕ 1⟩ | 00⟩ iσ y⊗ σ x | ψ 1⟩ | ϕ 1⟩ | 01⟩ I⊗ σ z | ψ 2⟩ | ϕ 1⟩ | 01⟩ I⊗ σ x | ψ 3⟩ | ϕ 1⟩ | 01⟩ iσ y⊗ I | ψ 4⟩ | ϕ 1⟩ | 01⟩ iσ y⊗ iσ y | ψ 1⟩ | ϕ 1⟩ | 10⟩ σ z⊗ I | ψ 2⟩ | ϕ 1⟩ | 10⟩ σ z⊗ iσ y | ψ 3⟩ | ϕ 1⟩ | 10⟩ σ x⊗ σ z | ψ 4⟩ | ϕ 1⟩ | 10⟩ σ x⊗ σ x | ψ 1⟩ | ϕ 1⟩ | 11⟩ σ z⊗ σ z | ψ 2⟩ | ϕ 1⟩ | 11⟩ σ z⊗ σ x | ψ 3⟩ | ϕ 1⟩ | 11⟩ σ x⊗ I | ψ 4⟩ | ϕ 1⟩ | 11⟩ σ x⊗ iσ y | ψ 1⟩ | ϕ 2⟩ | 00⟩ I⊗ σ z | ψ 2⟩ | ϕ 2⟩ | 00⟩ I⊗ σ x | ψ 3⟩ | ϕ 2⟩ | 00⟩ iσ y⊗ I | ψ 4⟩ | ϕ 2⟩ | 00⟩ iσ y⊗ iσ y | ψ 1⟩ | ϕ 2⟩ | 01⟩ I⊗ I | ψ 2⟩ | ϕ 2⟩ | 01⟩ I⊗ iσ y | ψ 3⟩ | ϕ 2⟩ | 01⟩ iσ y⊗ σ z | ψ 4⟩ | ϕ 2⟩ | 01⟩ iσ y⊗ σ x | ψ 1⟩ | ϕ 2⟩ | 10⟩ σ z⊗ σ z | ψ 2⟩ | ϕ 2⟩ | 10⟩ σ z⊗ σ x | ψ 3⟩ | ϕ 2⟩ | 10⟩ σ x⊗ I | ψ 4⟩ | ϕ 2⟩ | 10⟩ σ x⊗ iσ y | ψ 1⟩ | ϕ 2⟩ | 11⟩ σ z⊗ I | ψ 2⟩ | ϕ 2⟩ | 11⟩ σ z⊗ iσ y | ψ 3⟩ | ϕ 2⟩ | 11⟩ σ x⊗ σ z | ψ 4⟩ | ϕ 2⟩ | 11⟩ σ x⊗ σ x | ψ 1⟩ | ϕ 3⟩ | 00⟩ σ z⊗ I | ψ 2⟩ | ϕ 3⟩ | 00⟩ σ z⊗ iσ y | ψ 3⟩ | ϕ 3⟩ | 00⟩ σ x⊗ σ z | ψ 4⟩ | ϕ 3⟩ | 00⟩ σ x⊗ σ x | ψ 1⟩ | ϕ 3⟩ | 01⟩ σ z⊗ σ z | ψ 2⟩ | ϕ 3⟩ | 01⟩ σ z⊗ σ x | ψ 3⟩ | ϕ 3⟩ | 01⟩ σ x⊗ I | ψ 4⟩ | ϕ 3⟩ | 01⟩ σ x⊗ iσ y | ψ 1⟩ | ϕ 3⟩ | 10⟩ I⊗ I | ψ 2⟩ | ϕ 3⟩ | 10⟩ I⊗ iσ y | ψ 3⟩ | ϕ 3⟩ | 10⟩ iσ y⊗ σ z | ψ 4⟩ | ϕ 3⟩ | 10⟩ iσ y⊗ σ x | ψ 1⟩ | ϕ 3⟩ | 11⟩ I⊗ σ z | ψ 2⟩ | ϕ 3⟩ | 11⟩ I⊗ σ x | ψ 3⟩ | ϕ 3⟩ | 11⟩ iσ y⊗ I | ψ 4⟩ | ϕ 3⟩ | 11⟩ iσ y⊗ iσ y | ψ 1⟩ | ϕ 4⟩ | 00⟩ σ z⊗ σ z | ψ 2⟩ | ϕ 4⟩ | 00⟩ σ z⊗ σ x | ψ 3⟩ | ϕ 4⟩ | 00⟩ σ x⊗ I | ψ 4⟩ | ϕ 4⟩ | 00⟩ σ x⊗ iσ y | ψ 1⟩ | ϕ 4⟩ | 01⟩ σ z⊗ I | ψ 2⟩ | ϕ 4⟩ | 01⟩ σ z⊗ iσ y | ψ 3⟩ | ϕ 4⟩ | 01⟩ σ x⊗ σ z | ψ 4⟩ | ϕ 4⟩ | 01⟩ σ x⊗ σ x | ψ 1⟩ | ϕ 4⟩ | 10⟩ I⊗ σ z | ψ 2⟩ | ϕ 4⟩ | 10⟩ I⊗ σ x | ψ 3⟩ | ϕ 4⟩ | 10⟩ iσ y⊗ I | ψ 4⟩ | ϕ 4⟩ | 10⟩ iσ y⊗ iσ y | ψ 1⟩ | ϕ 4⟩ | 11⟩ I⊗ I | ψ 2⟩ | ϕ 4⟩ | 11⟩ I⊗ iσ y | ψ 3⟩ | ϕ 4⟩ | 11⟩ iσ y⊗ σ z | ψ 4⟩ | ϕ 4⟩ | 11⟩ iσ y⊗ σ x

Table 4. Charlie’ s recovery unitary operator UC conditioned on Alice’ s RA, Bob’ s RB, and Charlie’ s RC, where I is the identity operator and σ x, iσ y, σ z are Pauli matrices.

As an example, we might as well consider the situation that the result of Bob’ s PM_B is | ϕ ₂⟩ _B1B2, then based on Eq. (19), the state of particles C₁, C₂, C₃, and C₄ evolves as

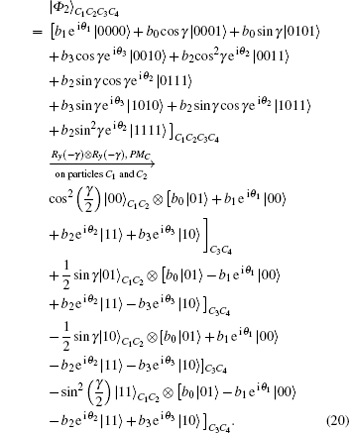
Note that after Charlie’ s PM_C, the state of particles C₃ and C₄ in Eq. (20) is perfectly correlated to the target state | χ ⟩ ₂. According to Alice’ s, Bob’ s and his own measurement results, Charlie can recover the target state | χ ⟩ ₂ by appropriate local unitary operations. In our discussion here, Alice’ s and Bob’ s measurement results are | ψ ₂⟩ _A1A2 | ϕ ₂⟩ _B1B2, if Charlie’ s measurement result is | 00⟩ _C1C2 with the probability of P_{RC| RARB} = cos⁴(γ /2), then U_C = I ⊗ σ _x is required to perform on particles C₃ and C₄, the target state | χ ⟩ ₂ can be readily reestablished, as shown in Table 4.

As a supplement, when it comes to the other three cases corresponding to Alice’ s projective measurement results | ψ ₁⟩ _A1A2, | ψ ₃⟩ _A1A2 and | ψ ₄⟩ _A1A2, there will be a similar analysis process. Here we no longer depict them one by one. According to Table 4, it is easily found that, for all the possible measurement results of Alice, Bob, and Charlie, the receiver Charlie is always able to reconstruct the target state | χ ⟩ ₂ by performing appropriate unitary operation U_C on particles C₃ and C₄. Thus, our JRSP scheme is deterministic. Mathematically, the total success probability reads

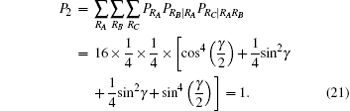
In summary, by constructing a set of ingenious four-particle partially entangled states to serve as the quantum channels, we have investigated deterministic JRSP of arbitrary single- and two-qubit states. Correspondingly, the quantum circuits for our JRSP schemes are designed. In this article, we deal with the JRSP from two senders to one receiver. Participants collaborate with each other, and perform projective measurements under an elaborate measurement basis on their own particles. Combined with the feed-forward technique adapted by senders, that is, before performing his projective measurement PM_B, Bob should perform a suitable unitary operation on his particles conditioned on the result of Alice’ s PM_A. This way, the receiver can reestablish the target state by means of appropriate local unitary operations with unit success probability. Furthermore, based on our research here, an extension to deterministic JRSP of general multi-qubit states is possible.

It needs emphasizing that, at variance with most existing JRSP protocols, in our schemes, the receiver plays quite an active role in the sense that he not merely performs the reconstruction operation at the end, his projective measurement result is equally useful as that of both senders. In addition, to accomplish the JRSP tasks, the initially shared partially entangled quantum channels are necessary, but unit success probability can always be achieved irrespective of the channel’ s entanglement degree. This point is very interesting and primarily meaningful considering the technological challenges to prepare and maintain maximal entanglement in real-word implementations.

Regretfully, there is a limitation lying in this paper. The achievement of the JRSP depends critically on the receiver’ s knowledge of the quantum channel, requiring the channel parameter γ to be constant during the JRSP procedure. After completing the preparation of the quantum channel, particles should be distributed to corresponding participants. During the distribution process, not simply the parameter γ but the quantum channel as a whole will be changed due to the unavoidable “ en route” decoherence. In fact, this is a limitation for almost all the existing JRSP protocols. To overcome this limitation, there is still a lot of work to do.