Cite this Article
Tian Li-Jun, Ti Min-Min, Zhai Xiang-Dong. Non-Markovianity of a qubit coupled with an isotropic Lipkin–Meshkov–Glick bath. Chinese Physics B, 24(10): 100305  
Permissions
Non-Markovianity of a qubit coupled with an isotropic Lipkin–Meshkov–Glick bath
Tian Li-Jun, Ti Min-Min, Zhai Xiang-Dong
Department of Physics, Shanghai University, Shanghai 200444, China

†Corresponding author. E-mail: tianlijun@staff.shu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 11075101).

Abstract

We study the non-Markovianity of the single qubit system coupled with an isotropic Lipkin–Meshkov–Glick (LMG) model by an effective method proposed by Breuer et al. (Breuer H P and Piilo J 2009 Europhys. Lett.85 5004). It is discovered that the non-Markovianity is concerned with the quantum phase transitions (QPTs). In the open system, we present that the strong coupling inside the bath and the strong interaction between the system and bath can enhance the degree of non-Markovianity. Moreover, the non-Markovianity is stronger and more sensitive for the bath in the symmetric phase than the symmetry broken phase.

PACS: 03.65.Yz; 05.45.–a; 75.10.Pq
Keyword: non-Markovianity; qubit dynamics; LMG model
1. Introduction

Unavoidable interaction between the realistic quantum systems and the environment makes the systems fragile.[1, 2] For this reason, more researchers are interested in the effect of the environment on the dynamics of the open quantum systems. According to the characteristic of the environment, the quantum dynamical processes can usually be classified into Markovian processes and non-Markovian processes. Markovian processes in which the information flows out monotonously from the system into the environment have no memory effect, while non-Markovian processes demonstrate the memory effect and tend to increase the distinguishability between any two states.[3] We quantify this memory effect by means of measuring the total information flowing back to the open system from the environment. When a system interacts with a weak system– environment coupling or a memoryless environment, it can be described by Markovian approximation. However, for the strong system– environment couplings or short timescales, Markovian approximation is invalid and some complicated non-Markovian properties appear in the dynamical processes.[1, 4]

Through varieties of analytical methods and numerical simulation techniques, researchers have found that the Markovian processes and non-Markovian processes have different effects on decoherence and disentanglement of open systems.[5– 11] Since then, the non-Markovian dynamics has become increasingly significant and interesting. In recent years, the non-Markovianity has been investigated in some physical systems, such as atomic and molecular systems, [12] high-Q cavity systems, [13] solid state physics, [14] etc. Many outstanding works have been explored.[4, 15– 19] Especially in quantum information processing, the non-Markovian dynamics has attracted much attention as a result of regaining lost information and recovering coherence for quantum technologies.

However, up to now, the rigid quantum extension definition of non-Markovianity is still vague. In order to quantify the degree of non-Markovianity, some methods have been proposed.[3, 20– 23] For example, Rivas et al. provided two methods respectively based on dynamical divisibility and entanglement.[22] Lu et al. quantified non-Markovianity by making use of the quantum Fisher information flow.[23] Based on the trace distance, Breuer et al. proposed a method to quantify the non-Markovian behavior of quantum processes in open systems, [3] and the method has been used in many different system– environment models such as spin chain, [24, 25] biomolecules, [26] ultracold quantum gases, [27] etc. What is more, as this measurement is not limited to the interaction structure between the system and the environment, it is more flexible to be applied to some experiments under real environments[28] or simulated reservoirs.[29]

The LMG model, first constructed to test the validity of various techniques and formalisms developed for treating many-particle systems, can be solved exactly in many cases.[30] This model consists of N spins distributed in two degenerate levels and each spin interacts with others. It can be used to describe a group of interactional spins in the x− y plane. The ground-state properties of a quantum system will be changed when quantum phase transitions (QPTs)[31] occur at absolute zero, which are induced by the change of external parameters or coupling constants. This kind of phase transition is often accompanied by the change of symmetry.[32] By adjusting the coupling constants, the LMG model will show two different phases, i.e., symmetric phase and symmetry broken phase. Correspondingly, the ground-states corresponding to the two phases have different properties.

Haikka et al. studied the non-Markovianity of a central qubit coupled to a quantum Ising ring in the transverse field.[33] They found that the central spin dynamics demonstrates purely Markovian dynamics in the QPTs point. Quantum phase transition and time-dependent purity in a central qubit coupled to an LMG bath have been studied and the results showed that the purity has distinctly different behavior in different phases.[34] In order to reveal the connection between the non-Markovianity and the symmetries of the phases, we study the non-Markovian dynamics of a single-qubit system coupled with an isotropic LMG bath. In this composite system, the coupling strength between the two subsystems cannot be ignored in comparison with the coupling strength between the spins in the environment. In this paper we explore that the non-Markovianity exhibits different behaviors in different phases.

This paper is organized as follows. In Section 2, we work out the reduced density matrix of the central qubit system, and quantify the non-Markovianity in accordance with the measurement proposed by Breuer et al.[9] In Section 3, we analyze the effects of coupling strengths and the spin number of the environment on the degree of non-Markovianity. Section 4 is the conclusion.

2. Methods and model
2.1. Methods

Based on the trace distance, an effective method to quantify the non-Markovianity of quantum processes in open systems has recently been presented by Breuer et al. The trace distance D describing the distinguishability between the two quantum states ρ 1 and ρ 2 is defined as[35]

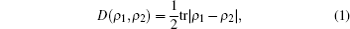
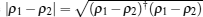
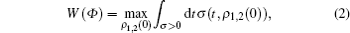
where and D satisfies 0 ≤ D ≤ 1.[2] The two states are the same for D = 0 and completely distinguishable for D = 1. In view of a dynamical quantum process Φ (t), one can get the quantum states ρ (t) at any time t > 0 with evolution from ρ (0). Then the non-Markovianity W quantifying the reflux information from the environment to the system can be defined as

where the change rate of the trace distance σ (t, ρ 1, 2(0)) is defined as

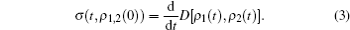
On one hand, if there are one pair of initial states and certain time t that makes σ (t, ρ 1, 2(0)) > 0, the distinguishability of the pair of states increases. In other words, if the trace distance D increases monotonously in certain time intervals, then the quantum process demonstrates a non-Markovian dynamics process. On the other hand, σ (t, ρ 1, 2(0)) ≤ 0 is corresponding to a Markovian dynamical process.

According to Eq.  (3), W can be rewritten as

The trace distance D is increasing monotonously in arbitrary time interval [an, bn]. If Wn is defined as the difference of D between the local maximum and local minimum for arbitrary time interval [an, bn], it can be written as follows:

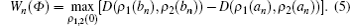
Clearly, it is much easier to obtain the maximal value of Wn in Eq.  (5) than W in Eq.  (4). Based on this idea, we will measure the non-Markovianity of the single qubit coupled to an isotropic LMG bath in this article.

2.2. Single-qubit coupled to an isotropic LMG bath

The total Hamiltonian of a qubit coupled with the LMG bath model can be written as[34, 36– 40]

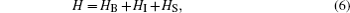
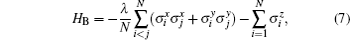
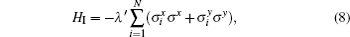
HS is the Hamiltonian of the central qubit. HB is the Hamiltonian of the isotropic LMG model. λ denotes the coupling strength between the spins in the bath environment, and is inversely proportional to the external magnetic field strength. N is the spin number of the bath. HI denotes the interaction between the central quantum system and the environment, and λ ′ is the coupling strength between the central qubit and the bath. 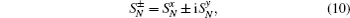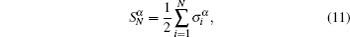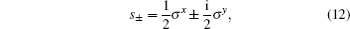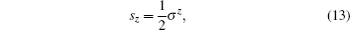σ α and are the Pauli matrices of the central qubit and the i-th spin in the environment respectively. Through the following transformation,

where 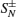, s± are the ladder operators of the N-spin bath and the central qubit respectively, the total Hamiltonian in the Dicke representation can be rewritten as

In terms of the LMG bath model, λ = 1 is the QPT point. When 0 < λ < 1, all the spins in the bath polarized in the external magnetic field direction, and the symmetry is broken. So the bath is in the symmetry broken phase, and the ground state is | G〉 = | N/2, N/2〉 . When λ > 1, the external magnetic field strength is not large enough to break the symmetry, so the bath is in the symmetric phase and the ground state is | G〉 = | N/2, M〉 , where M is the integer nearest to N/2λ .

2.3. The non-Markovianity W of symmetric phase (λ > 1)

We can assume the LMG model is in the ground state ρ E = | G〉 〈 G| , and the single qubit system is in an initial state

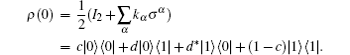
The initial state of the composite system can be written as ρ tot(0) = ρ (0) ⊗ ρ E.

The evolutional state of the composite system is resolved by ρ tot(t) = U(t)ρ tot(0)U† (t), where the dynamical evolution operators U(t) = e− iHt. In order to obtain the reduced states of the central qubit, one needs to trace out the environment,

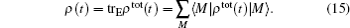
The reduced states of the central qubit in a symmetric phase is

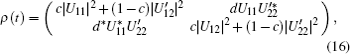
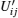
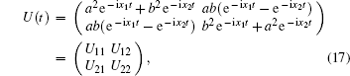
where Uij, denote the dynamical evolution operators of invariant subspace HM, HM− 1 respectively. In an invariant subspace HM of H spanned by the ordered basis vector {| N/2, M〉 ⊗ | 0〉 , | N/2, M + 1〉 ⊗ | 1〉 }, U(t) = e− iHt can be expressed as follows:

where

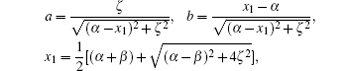
and

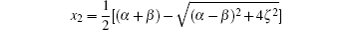
are the two eigenvalues of HM. Here

When M = N/2, | N/2, N/2〉 ⊗ | 0〉 is an eigenstate of the total Hamiltonian corresponding to the eigenenergy of − (N + 1). So {| N/2, M〉 ⊗ | 0〉 } is a one-dimensional invariant subspace, and the above dynamic evolution is only applied when − N/2 ≤ M < N/2.

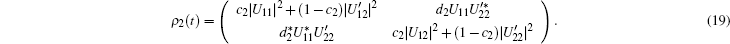
We assume two initial qubit states and . According to Eq.  (16), we can get the two evolutional states,

Then, we calculate the trace distance D of the two states according to Eq.  (1)

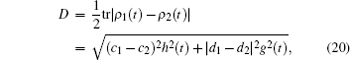
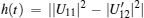
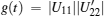
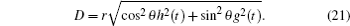
where , denote the amplitude of the evolution states. Setting c1 − c2 = r cos θ , d1 − d2 = reiϕ sin θ (r ≤ 1, θ ∈ [0, 2π ] and φ ∈ [0, π ]), equation  (20) can be rewritten as

According to Eq.  (5), we can obtain

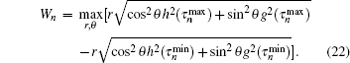
When θ = π , r = 1, the maximum values of Wn is

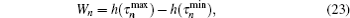
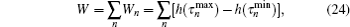
and .

2.4. The non-Markovianity W of symmetry broken phase (0 < λ < 1)

In symmetry broken phase, the ground state of the environment is | G〉 = | N/2, N/2〉 . | G〉 ⊗ | 0〉 is the eigenstate of the total Hamiltonian, and the corresponding eigenenergy is − (N + 1). {| N/2〉 ⊗ | 1〉 , | N/2 − 1〉 ⊗ | 0〉 } is a two-dimensional invariant subspace. In the same way, we can get the evolutional states,

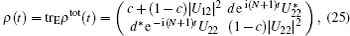
the trace distance of the two evolutional states

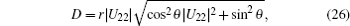
where c1 − c2 = r cos θ , d1 − d2 = reiϕ sin θ , (r ≤ 1, θ ∈ [0, 2π ], and φ ∈ [0, π ]), and

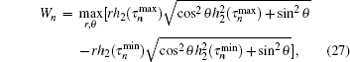
where h2(τ ) = | U22| . By calculating, when θ = π , r = 1, Wn takes the maximum values,

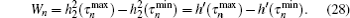
As h′ (τ ) = | U22| 2, we can obtain

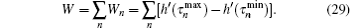
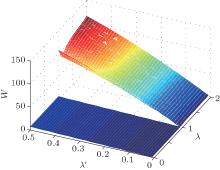
3. Effect of the bath on non-Markovianity

Figure 1 shows the effects of λ and λ ′ on the degree of non-Markovianity W in the two different phases. Apparently, in the symmetric phase (1 < λ < 2), the system shows a strong non-Markovianity, while in the symmetry broken phase it demonstrates an extremely weak non-Markovianity. It indicates that there is more information flowed back to the system from the environment in the symmetric phase than in the other. In order to interpret this phenomenon, we need to study how these parameters affect the oscillatory behaviors of h(t) or h′ (t) in the two different phases respectively.

Fig.  1. The non-Markovianity W as function of λ and λ ′ for N = 500.

Equations  (24) and (29) show that the degree of non-Markovianity W depends on the amplitude of the evolution states h(t) or h′ (t). So the behaviors of h(t) or h′ (t) will determine the non-Markovian dynamical process. According to the h(t) and h′ (t), the effects of the bath parameters (λ , λ ′ , and N) on the degree of non-Markovianity are studied in the following.

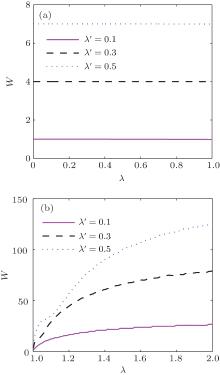
First of all, in order to elucidate how the coupling strength λ affects the non-Markovianity in the two phases respectively, we plot Fig. 2 with the different λ ′ . The curves demonstrate that the coupling strength λ between spins in the environment merely has no influence on the non-Markovanity W in symmetry broken phase as shown in Fig. 2(a), but figure 2(b) shows that the degree of non-Markovianity increases when the coupling strength λ gets stronger. That means more information will reverse to the system from the environment if the coupling strength between the spins in the environment increases in the symmetric phase. Furthermore, when 1.1 < λ < 2, the increasing trend of W becomes smooth, while 1 < λ < 1.1, W increases sharply as shown in Fig. 2(b). In light of the oscillatory behavior of the amplitude function of the evolutional states h(t) and h′ (t), we will illustrate this interesting phenomenon by Fig. 3 and Fig. 4.

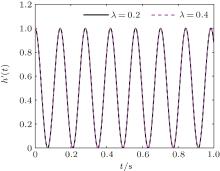Fig.  2. The non-Markovianity versus the different phases for different values of λ ′ with N = 500.

Fig.  3. The amplitude of evolution state h′ (t) versus time t with different λ in the case of N = 500, λ ′ = 0.5.

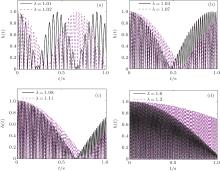Fig.  4. The curves of h(t) versus time t with different λ are plotted in panels (a), (b), (c), and (d) for N = 500, λ ′ = 0.5.

In Fig. 3, the curves show the oscillatory dynamics of amplitude function h′ (t) versus that in the symmetry broken phase. The oscillation is stable without decay and has nothing to do with λ . The number of h′ (t)’ s increasing intervals is unchanged however λ changes in the fixed parameter space. So the degree of non-Markovianity is invariable even if the coupling strength changes, which is consistent with Fig. 2(a). The curves in Fig. 4 exhibit the oscillatory dynamics of amplitude function h(t) in the symmetric phase. Apparently, the oscillatory behavior of this function is complicated and different from the symmetry broken phase. When 1.1 < λ < 2 (Fig. 4(d)), as the parameter increases, the oscillation frequency is increasing, but the oscillation amplitude is decreasing. What is more, the larger the λ , the slower the decreasing trend. When 1 < λ < 1.1, that is a complicated oscillatory behavior. As λ gets larger, the oscillation frequency increases (Figs. 4(a), 4(b), and 4(c)). Because the oscillatory behavior is different, the increasing rate of the degree of non-Markovianity is also distinct (Fig. 2(b)). The results show that the oscillatory behavior of the amplitude function h(t) gets bigger if we increase λ , i.e., h(t) has much more increasing intervals in the fixed time interval. Hence, the non-Makovianity gets stronger in the symmetric phase.

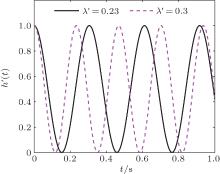
Next, we discuss the effects of the parameter λ ′ on the non-Markovianity in the symmetry broken phase in Fig. 5(a) and the symmetric phase in Fig. 5(b) respectively. From Fig. 5, we get that the degree of non-Markovianity W increases with increasing λ ′ . The evolution of W shows the very interesting ladder shaped growth in the symmetry broken phase. When the coupling interaction between the system and the environment becomes stronger, the reflux information is invariable in some intervals, while in other intervals, the reflux information is more. This phenomenon is concerned with the oscillatory behavior of amplitude function h′ (t). Figure 6 demonstrates the oscillatory behavior of amplitude function h′ (t) for two different values of λ ′ . As λ ′ adds 0.07, the amplitude function adds a period. So we can gain that the period of this function in our fixed parameter space is nearly 0.07. According to the definition of non-Markovianity, W is a summation of h′ (t) in increasing intervals. So as λ ′ adds 0.035, h′ (t) will increase half a period. If h′ (t) is monotonic increasing in this interval, the degree of non-Markovianity will increase, otherwise it remains the same. That is why the degree of non-Markovianity increases by ladder shape.

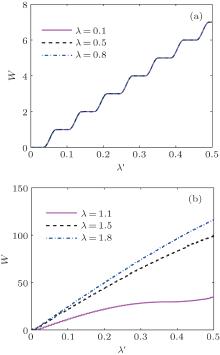Fig.  5. Setting N = 500, the non-Markovianity versus λ ′ are plotted in panels (a) and (b) with different λ : (a) λ = 0.1, 0.5, and 0.8; (b) λ = 1.1, 1.5, and 1.8.

Fig.  6. h′ (t) versus time t with λ ′ = 0.23 and 0.3 when N = 500, λ = 0.6.

The curves in Fig. 5(b) show how the coupling strength between the system and the environment affect the non-Markovianity in the symmetric phase. As the coupling strength gets stronger, the degree of non-Markovianity increases. Apparently, the degree of the non-Markovianity in this phase is powerful. The curve trend of λ = 1.1 is drastic. The total trend is increasing but the growth rate becomes slow. We will resolve this case by Fig. 7. As the coupling interaction between the system and the environment becomes strong, the frequency of the oscillatory increases and h(t) shows a damped amplitude oscillation. Hence, the degree of non-Markovianity increases but the growth rate decreases.

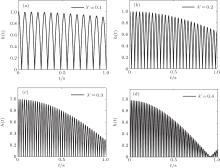Fig.  7. The curves of h(t) versus t with different λ ′ are plotted in (a) λ ′ = 0.1, (b) λ ′ = 0.2, (c) λ ′ = 0.3, (d) λ ′ = 0.4 in the case of N = 500, λ = 1.1.

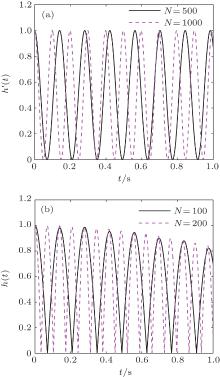
At last, we discuss the effects of the total spin number N on the degree of non-Markovianity in the two different phases. From Fig. 8, we can find that the effects of N in the two phases are similar. The reflux information is all distinctly increasing as the number of spins in the environment increases. Enlarging N, the frequency of the amplitude function in both phases increases, as shown in Fig. 9. In the fixed time interval [0, 1s], more increasing intervals appear. Hence, the degree of non-Markovianity increases and more information reversed from the environment.

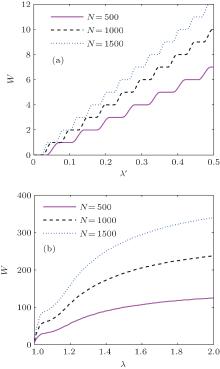Fig.  8. The non-Markovianity versus λ ′ with different values of N. N = 500 (solid line), N = 1000 (dashed line), N = 1500 (dotted line). (a) λ = 0.8. (b) λ ′ = 0.5.

Fig.  9. The oscillatory behaviors of amplitude function in different phases. (a) λ = 0.4, λ ′ = 0.5, N = 500 (solid line), N = 1000 (dashed line). (b) λ = 1.2, λ ′ = 0.2, N = 100 (solid line), N = 200 (dashed line).

4. Conclusion

In this paper, we discussed the non-Markovianity of the single qubit coupled to an isotropic LMG bath with the method proposed by Breuer and co-workers. On both sides of the QPT point in the LMG bath, the memory effect of the central qubit has obvious differences as a result of the different oscillatory behaviors of the amplitude function. In the symmetric phase (λ > 1), the memory effect is strong and much information reversed from the environment to the central qubit system, while the memory effect is tremendously weak in symmetry-broken phase (0 < λ < 1). In the symmetry broken phase, the amplitude function is a constant amplitude oscillation with low oscillatory frequency. In the symmetric phase, the amplitude function has a complicated oscillatory behavior, i.e., when λ > 1.1, the amplitude function shows an amplitude-damped oscillation; the oscillatory frequency becomes higher than that of the other phase. Hence, the non-Markovianity is strong in the symmetric phase and weak in the symmetry-broken phase. We then analyze the effect of three parameters (λ , λ ′ , and N) on the non-Markovianity in the two different phases. We find that the symmetric phase is more sensitive than the symmetry-broken phase for these parameters. λ enhances the memory effect by increasing the oscillatory frequency and decreasing the amplitude-damped rate of the amplitude function in the symmetric phase, while it hardly has influence in the memory effect in the symmetry-broken phase. λ ′ modulates the memory effect of the central qubit system via changing the oscillatory period in the symmetry-broken phase, but enlarging λ ′ can also make the non-Markovianity powerful by increasing the oscillatory frequency and the amplitude-damped rate of the amplitude function in the symmetric phase. The number of spins N in the environment enhances the non-Markovianity degree by modifying the oscillatory period in both phases. Our results are helpful for studying the non-Markovian processes and may have potential applications in the quantum information field.

Reference
1 Breuer H P and Petruccione F 2002 The Theory of Open Quantum Systems Oxford Oxford University Press [Cited within:2]
2 Gardiner C W and Zoller P 2004 Quantum Noise Berlin Springer-Verlag [Cited within:2]
3 Breuer H P, Laine E M and Piilo J 2009 Phys. Rev. Lett. 103 210401 DOI:10.1103/PhysRevLett.103.210401 [Cited within:3]
4 Xiang J D, Qin L G and Tian L J 2014 Chin. Phys. B 23 110305 DOI:10.1088/1674-1056/23/11/110305 [Cited within:2]
5 Strunz W T, Diosi L and Gisin N 1999 Phys. Rev. Lett. 82 1801 DOI:10.1103/PhysRevLett.82.1801 [Cited within:1]
6 Budini A A 2000 Phys. Rev. A 63 012106 DOI:10.1103/PhysRevA.63.012106 [Cited within:1]
7 Garraway B M 1997 Phys. Rev. A 55 2290 DOI:10.1103/PhysRevA.55.2290 [Cited within:1]
8 Piilo J, Maniscalco S, Harkonen K and Suominen K A 2008 Phys. Rev. Lett. 100 180402 DOI:10.1103/PhysRevLett.100.180402 [Cited within:1]
9 Breuer H P and Piilo J 2009 Europhys. Lett. 85 50004 DOI:10.1209/0295-5075/85/50004 [Cited within:1]
10 Breuer H P and Vacchini B 2008 Phys. Rev. Lett. 101 140402 DOI:10.1103/PhysRevLett.101.140402 [Cited within:1]
11 Wolf M M, Eisert J, Cubitt T S and Cirac J I 2008 Phys. Rev. Lett. 101 150402 DOI:10.1103/PhysRevLett.101.150402 [Cited within:1]
12 Hamm P, Lim M and Hochstrasser R M 1998 Phys. Rev. Lett. 81 5326 DOI:10.1103/PhysRevLett.81.5326 [Cited within:1]
13 Dublin F, Rotter D, Mukherjee M, Russo C, Eschner J and Blatt R 2007 Phys. Rev. Lett. 98 183003 DOI:10.1103/PhysRevLett.98.183003 [Cited within:1]
14 Lai C W, Maletinsky P, Badolato A and Imamoglu A 2006 Phys. Rev. Lett. 96 167403 DOI:10.1103/PhysRevLett.96.167403 [Cited within:1]
15 Tang N, Xu T T and Zeng H S 2013 Chin. Phys. B 22 030304 DOI:10.1088/1674-1056/22/3/030304 [Cited within:1]
16 Ding B F, Wang X Y, Tang Y F, Mi X W and Zhou H P 2011 Chin. Phys. B 20 060304 DOI:10.1088/1674-1056/20/6/060304 [Cited within:1]
17 Zheng Y P, Tang N, Wang G Y and Zeng H S 2011 Chin. Phys. B 20 110301 DOI:10.1088/1674-1056/20/11/110301 [Cited within:1]
18 Zou H M, Fang M F and Yang B Y 2013 Chin. Phys. B 22 120303 DOI:10.1088/1674-1056/22/12/120303 [Cited within:1]
19 Fan Z L, Tian J and Zeng H S 2014 Chin. Phys. B 23 060303 DOI:10.1088/1674-1056/23/6/060303 [Cited within:1]
20 Luo S L, Fu S S and Song H T 2012 Phys. Rev. A 86 044101 DOI:10.1103/PhysRevA.86.044101 [Cited within:1]
21 Gang J, Zou J and Shao B 2010 Phys. Rev. A 81 062124 DOI:10.1103/PhysRevA.81.062124 [Cited within:1]
22 Rivas A, Huelga S F and Plenio M B 2010 Phys. Rev. Lett. 105 050403 DOI:10.1103/PhysRevLett.105.050403 [Cited within:1]
23 Lu X M, Wang X G and Sun C P 2010 Phys. Rev. A 82 042103 DOI:10.1103/PhysRevA.82.042103 [Cited within:2]
24 Apollaro T J G, DiFranco C, Plastina F and Paternostro M 2011 Phys. Rev. A 83 032103 DOI:10.1103/PhysRevA.83.032103 [Cited within:1]
25 Lorenzo S, Plastina F and Paternostro M 2011 Phys. Rev. A 84 032124 DOI:10.1103/PhysRevA.84.032124 [Cited within:1]
26 Rebentrost P and Aspuru G A 2011 J. Chem. Phys. 134 101103 DOI:10.1063/1.3563617 [Cited within:1]
27 Haikka P, McEndoo S, DeChiara G, Palma G M and Maniscalco S 2011 Phys. Rev. A 84 031602 DOI:10.1103/PhysRevA.84.031602 [Cited within:1]
28 Vahala K J 2003 Nature 424 839 DOI:10.1038/nature01939 [Cited within:1]
29 Buluta I and Nori F 2009 Science 326 108 DOI:10.1126/science.1177838 [Cited within:1]
30 Lipkin H J, Meshkov N and Glick A J 1965 Nucl. Phys. 62 188 DOI:10.1016/0029-5582(65)90862-X [Cited within:1]
31 Sachdev S 2000 Quantum Phase Transitions Cambridge Cambridge University Press [Cited within:1]
32 Qian X F, Shi T, Li Y, Song Z and Sun C P 2005 Phys. Rev. A 72 012333 DOI:10.1103/PhysRevA.72.012333 [Cited within:1]
33 Haikka P, Goold J, McEndoo S, Plastina F and Maniscalo S 2012 Phys. Rev. A 85 060101 DOI:10.1103/PhysRevA.85.060101 [Cited within:1]
34 Quan H T, Wang Z D and Sun C P 2007 Phys. Rev. A 76 012104 DOI:10.1103/PhysRevA.76.012104 [Cited within:2]
35 Nielsen M A and Chuang I L 2000 Quantum Computation and Quantum Information Cambridge Cambridge University Press [Cited within:1]
36 Yuan X Z and Zhu K D 2005 Europhys. Lett. 69 868 DOI:10.1209/epl/i2004-10448-2 [Cited within:1]
37 Xu Z Y, Yang W L and Feng M 2010 Phys. Rev. A 81 044105 DOI:10.1103/PhysRevA.81.044105 [Cited within:1]
38 Yuan X Z, Zhu K D and Wu Z J 2005 Eur. Phys. J. D 33 129 DOI:10.1140/epjd/e2005-00023-y [Cited within:]
39 Ma X S, Wang A M, Yang X D and You H 2005 Phys. A 38 2761 DOI:10.1088/0305-4470/38/12/016 [Cited within:1]
40 Hamdouni Y, Fannes M and Petruccione F 2006 Phys. Rev. B 73 245323 DOI:10.1103/PhysRevB.73.245323 [Cited within:1]