In the late 1940s Shannon proposed the idea of assigning probabilities to the outcome of uncertain events and introduced the information entropy to measure the uncertainty.^[1] This concept has crossed a lot of barriers between traditionally separated disciplines and became a universal concept of statistical physics.^{[2– 6]} In 1975, Beckner, Bialynicki– Birula, and Mycieslki obtained an entropic uncertainty relation^{[7, 8]} as S_x + S_p ≥ D(1 + ln π ), where D represents the spatial dimension. In the one-dimensional case, the position– space (S_x) and momentum– space (S_p) information entropies are defined, respectively, by

where ψ (x) is a normalized eigenfunction in spatial coordinates and ϕ (p) is its normalized Fourier transform. It should be pointed out that the interval of the integration with respect to the variable x depends on the concrete quantum system.

Apart from their own significance, the entropic uncertainty relations have been utilized widely in both physics and chemistry.^{[9– 13]} Up to now, we have recognized that it is difficult to obtain explicit and analytical expressions for the formulas (1) due to the logarithmic factors in the integrals. At most they can be obtained analytically only for a few low-lying states of the harmonic oscillator, ^{[1, 14]} the Pö schl– Teller potential, ^{[15, 16]} the Morse potential, ^{[15, 17]} the Coulomb potential in high excited states, ^[18] as well as position– space entropy for the potential isospectral to the Pö schl– Teller potential, ^[19] several classical orthogonal polynomials, ^{[20– 22]} and other studies.^{[23– 25]} The main reason why the high lying states cannot be treated is from the difficulty in their Fourier transforms. We have to say that the above studies are done for those well-known physical potentials. Except for them, we have studied the quantum information entropies for some interesting and particular quantum systems, which are not familiar to general readers, such as the symmetrically and asymmetrically trigonometric Rosen– Morse potential, ^{[26, 27]} the Pö schl– Teller-like potential, ^[28] a squared tangent potential, ^[29] hyperbolic-type potential, ^[30] and hyperbolic double-well potential.^[31] It should be pointed out that almost all contributions to this topic have been done only in the constant mass Schrö dinger equation case^{[1– 31]} except for Ref. [32], in which we have studied the position-dependent mass Schrö dinger equation with a null potential. In this work, we attempt to study the Shannon entropy for the position-dependent mass Schrö dinger equation for a particle with a nonuniform solitonic mass density in the case of a hyperbolic-type potential.

The present paper is organized as follows. In Section 2 we present exact solutions of the system. In Section 3 we illustrate position and momentum information entropy densities, ρ _s(x) and ρ _s(p), respectively, and probability density ρ (x). We study S_x and S_p numerically for those six lowest-lying states. We find that the S_x entropy becomes negative beyond a particular mass width a due to the highly localized probability densities. Notice that the momentum information entropy S_p first increases with the parameter a and then decreases with it. Some concluding remarks are given in Section 4.

The non-ambiguous position-dependent mass Schrö dinger equation can be written as^{[33– 37]}

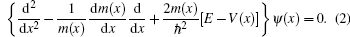
In the present study, we choose the following smooth effective mass distribution,

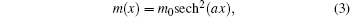
which is a suitable representative of a solitonic profile[36, 37] found in several effective models of condensed matter and low-energy nuclear physics. It is shown in Fig. 1 that the position-dependent mass is symmetric with respect to the variable x. Clearly, the mass barrier width is inversely proportional to the parameter a. In this case, if we take y = ax then the effective differential equation reads

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Position-dependent mass as a function of the position x.

Defining ψ (y) = cosh^v (y)ϕ (y) and substituting it into the above equation leads to

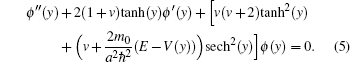
The transformation

maps y ∈ (− ∞ , ∞ ) → z ∈ (− π /2, π /2). The corresponding equation becomes

In the derivation of Eq. (6), we have used the following useful relations

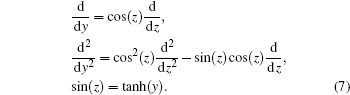
If choosing v = − 1/2, we obtain

Thus, equation (6) is equivalent to a regular constant-mass stationary Schrö dinger equation (8) for a particle of mass m₀ in a confining potential

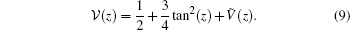
In order to make Eq. (8) soluble, we may take V(z) = − (3a²ħ ²/(8m₀)) sinh²(x) − a²ħ ²/(4m₀) in order to cancel the second term in if we use the relation sinh(x) = tan(z). In order to study the Shannon information entropy, let us write down the symmetric and antisymmetric solutions in the z space[35]

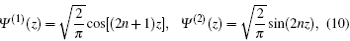
which, in turn, yield the solutions in the x space

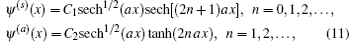
with the energy levels ε ∝ n² (n = 0, 1, 2, 3, … .).

For convenience, we list a few lowest-lying normalized states to calculate the Shannon information entropy

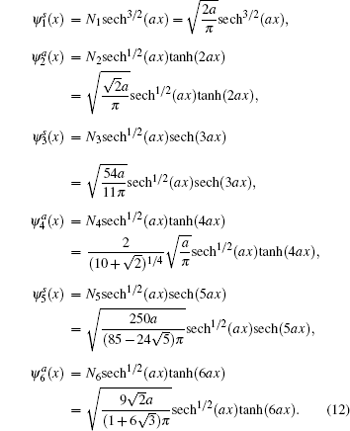
We give a useful remark about the solutions listed above. The analytical and explicit solutions have been obtained by Cunha and Christiansen in Ref. [35], but we have to point out that the solution ψ ₁(x) for the special case n = 0 was not discussed. A possible reason is that this case was not considered from the energy level, i.e., ε = 0. In fact, it is known that such a quantum state with zero energy is very special and is also important in studying the relation between the number of bound states and the scattering phase shifts. This kind of phenomenon is called the Levinson theorem.^{[38, 39]} If the wave function with the zero-energy is square integral and it tends to zero at infinity, this solution is physically acceptable. Otherwise, it is called a half bound state, which is not a bound state. On the other hand, we notice that the wave functions in the x space, the number of the nodes of the wave functions are broken. This is unlike that in the usual quantum systems. We show the wave functions in Figs. 2 and 3. Notice that the basic variations of the wave functions are very similar since the change of the parameter a directly modifies the range of the variable x.

Fig. 2.

	Figure Option ViewDownloadNew Window
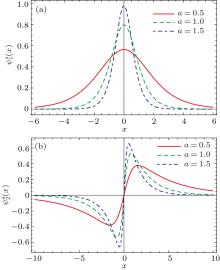	Fig. 2. Wave functions of the first (a) and second (b) states with definite parity depending on the parameter a as a function of the position x.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Wave functions (a = 1) with definite parity as a function of the position x.

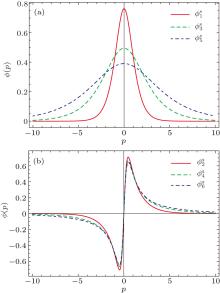
The position- and momentum-space information entropies for the one-dimensional potential can be calculated by using Eqs. (1). In general, explicit derivations of the information entropy are quite difficult. We have to study them numerically. In order to calculate the momentum information entropy, one has to transform the wave functions obtained in position space to momentum space using the Fourier transform. We also illustrate the position and momentum information entropy densities ρ _s(x) = | ψ (x)| ² ln | ψ (x)| ² and ρ _s(p) = | ϕ (p)| ² ln | ϕ (p)| ², since they play a similar role as the probability density ρ = | ψ (x)| ² in quantum mechanics.

Due to the difficulty in calculating wave functions in momentum space, we only consider a few lowest states. For example, using the wave functions of the ground state, we can derive the corresponding momentum representation through the Fourier transform

where p₁ = p/a (also below) and F₁(a; b, c; d; − 1; − i, i) represents the Appell function.

For the excited state n = 2, after some complicated algebraic manipulations we have

where

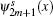
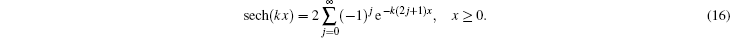
To obtain the analytical Fourier transforms of the high lying states n = 3− 6, we have to choose different approaches to treat the symmetrical and antisymmetrical solutions. For the symmetrical solutions , considering their parity property, we use the following formula^[40] for the sech(x) to study the Fourier transform

In this case, we are able to study this kind of integral (k = 2m + 1) as follows:

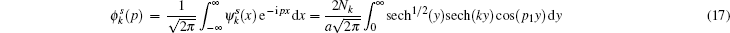
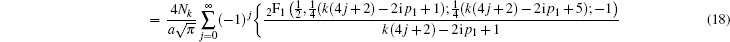
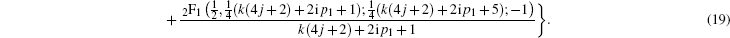
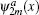
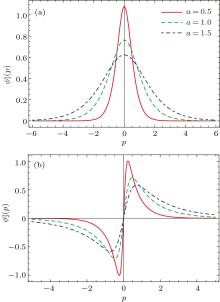However, for the wave functions with odd parity, says , their Fourier transforms become very complicated. For simplicity we do not list them here. The wave functions in the momentum space are displayed in Figs. 4 and 5.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Wave functions in momentum space for the first (a) and second (b) states with definite parity depending on the parameter a as a function of the momentum p.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Wave functions (a = 1) with definite parity as a function of the momentum p.

Characteristic features of the position and momentum probability densities are displayed in Figs. 6 and 7. We find that ρ (x) for the states n = 1, 3, 5 is greater than 1 at positions x = 0. This is not surprising since the most of the density is less than 1, the curve has to rise higher than 1 in order to have a total area of 1 as required for all probability distributions. Let us explain this in some detail. As pointed out by Catalá n et al., ^[41] this situation is mathematically possible, but it is unfound from a physical point of view when we consider the features of extension of a statistical measures of complexity introduced by LMC^[42] is extended to continuous systems.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Position– space densities (a = 1) for the n = 1– 6 eigenstates as a function of the position x.

Fig. 7.

	Figure Option ViewDownloadNew Window
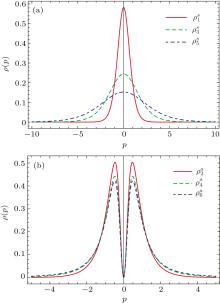	Fig. 7. Momentum– space densities (a = 1) for the n = 1– 6 eigenstates as a function of the momentum p.

We find that the maximum amplitudes of ρ (x) increase with the high excited states. On the other hand, we show the position and momentum entropy densities ρ _s(x) and ρ _s(p) in Figs. 8 and 9 with the parameter a = 1. It is found that the behavior of the maximum amplitude of the ρ _s(p) is contrary to that of ρ _s(x). Specially, we find that ρ _s(x) and ρ _s(p) for n = 2, 4, 6 are equal to zero at x = p = 0 since all the wave functions both in the position x and both in the momentum p are zero. We notice that all of them are symmetric with respect to the variable x. This arises from the symmetric mass barrier as well as the chosen potential sinh²(x) which we study here. In short, narrower mass barriers yield entropy densities that are more (less) localized in position (momentum) space. It should be addressed that the behaviors of the ρ _s and ρ both in the position and momentum in the case of the various parameter values a are very similar to those in the case a = 1. We do not show them for simplicity.

Fig. 8.

	Figure Option ViewDownloadNew Window
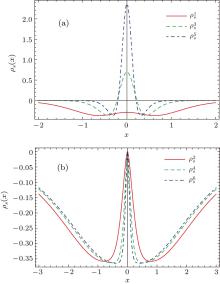	Fig. 8. Position– space entropy probability densities (a = 1) for the n = 1– 6 eigenstates as a function of the position x.

Fig. 9.

	Figure Option ViewDownloadNew Window
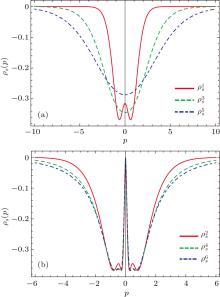	Fig. 9. Momentum– space entropy probability densities (a = 1) for the n = 1– 6 eigenstates as a function of the momentum p.

In Fig. 10, we show the position information entropy S_x as a function of the parameter a and find that it decreases with this parameter. With increasing a, the mass barrier becomes narrower, thus the time that the moving particle passes it becomes shorter, the system becomes more stable. Beyond some value a, the S_x becomes negative. This means that the physical “ object” , with nonuniform distributed solitonic mass, condenses or rather falls into order in a greater degree. For a fixed, the S_x decreases with the energy levels. That is to say, when the energy of the system increases, the quantum system becomes more localized in the position space. In particular, we find that the momentum space Shannon entropy S_p first increases with the parameter a and then decreases with it.

Fig. 10.

	Figure Option ViewDownloadNew Window
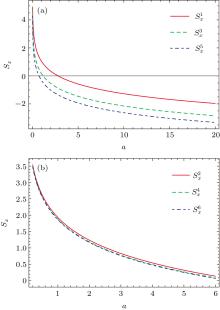	Fig. 10. Position information entropy Sx as a function of the parameter a for the n = 1− 6 eigenstates.

In Table 1 we present the numerical results of the information entropies S_x, S_p, and their sum for the low-lying six states and various parameter values a. The behavior coincides with that illustrated in Figs. 10 and 11. Particularly, we find that the system entropy could become negative for some given parameter values a. How to understand the negative entropy? It might be understood that the moving particle becomes condensed so that it does not move at all. The system becomes more stable at this moment. Note that with the increasing S_p, the S_x decreases but only to the extent that their sum stays above the stipulated lower bound of the value (1 + lnπ ).

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Momentum information entropy Sp as a function of the parameter a for the low-lying states.

Table 1.

Table 1.

Table 1. Information entropies of the n = 1− 6 eigenstates for different a values. n a Sx Sp Sx + Sp 1 + lnπ 1 3 – 0.033794 2.22242 2.18862 2.1447 4 – 0.177635 2.51006 2.33243 2.1447 2 3 0.414986 2.4789 2.89389 2.1447 4 0.271145 2.76658 3.03773 2.1447 3 3 – 0.472847 3.10422 2.63137 2.1447 4 – 0.616688 3.39107 2.77438 2.1447 4 3 0.38901 2.72818 3.11719 2.1447 4 0.245168 3.01412 3.25929 2.1447 5 3 – 0.711698 3.57848 2.86678 2.1447 4 – 0.855539 3.83539 2.97985 2.1447 6 3 0.381358 2.84722 3.22858 2.1447 4 0.237517 3.12399 3.36151 2.1447

Table 1. Information entropies of the n = 1− 6 eigenstates for different a values.

In this paper we have presented the Shannon entropy for the position and momentum eigenstates of the position-dependent Schrö dinger equation for a particle with a nonuniform solitonic mass density in the case of a hyperbolic-type potential. The position S_x and momentum S_p information entropies for n = 1− 6 are calculated. The fact that the S_x might be negative arises from the probability densities that are highly localized. We find that the position information entropy S_x decreases for narrower mass widths (larger a values), but the behavior of S_p first increases with the parameter a and then decreases with it. The mass barrier being inversely proportional to the a parameter determines the stability of the system. Some interesting features of the information entropy densities, ρ _s(x) and ρ _s(p), are demonstrated. The Bialynicki– Birula– Mycielski (BBM) inequality is also verified for a number of states. Before ending this work, we give a few useful remarks on the Shannon information entropy for the Schrö dinger equation with a constant mass or with a position-dependent mass case. Generally speaking, the quantum systems with a constant mass could be solved rather easily in comparison with those with a position-dependent mass. As we know, most of quantum systems with well-known physical potentials have been solved (see, e.g., Refs. [1]– [31]), but the quantum systems with a position-dependent mass become rather complicated because of the non-commutative property between the operator ∇ = d/dx and m(x) as shown in Eq. (2). Therefore, it is not easy to obtain the exact solutions of those quantum systems with a position-dependent mass even for those simplest cases as studied in Ref. [32] and in the present work. Nevertheless, the good points for position-dependent mass case lie in providing us for some new features of the Shannon information entropy related to the mass barrier width. On the other hand, let us give a brief comparison of the studies performed in Ref. [32] and in the present work. When we consider the effective potential (9) which is obtained by some suitable canonical transforms, the different choices of the V(z) determine different properties of studied quantum system, i.e., the solutions will be totally different. For instance, we choose V(z) = 0 in Ref. [32] and call it as the so-called null potential. However, in this work we choose V(z) as the present form (see below Eq. (9)) in order to make this system soluble. The different solutions given both in Ref. [32] and in this work result in the different properties of the Shannon entropy.