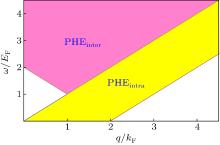
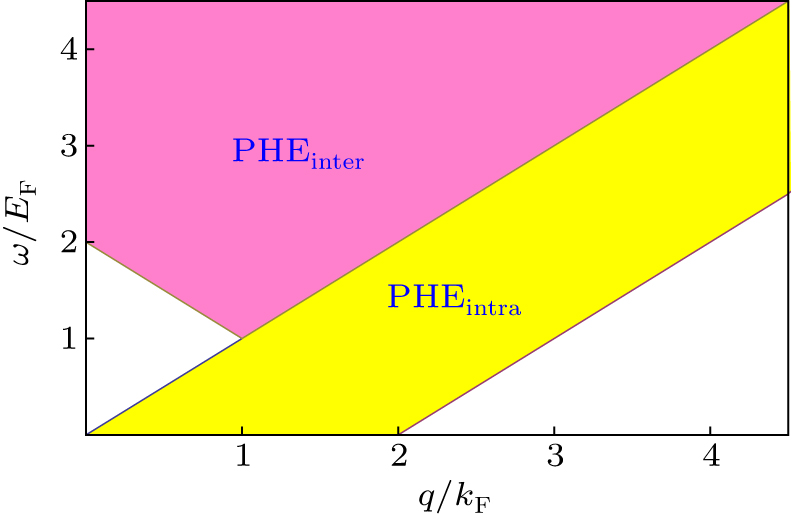
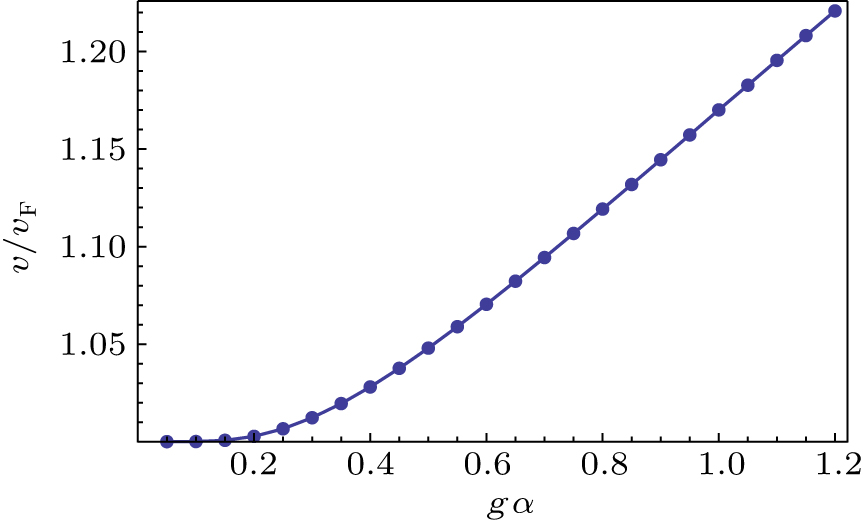
Collective modes of Weyl fermions with repulsive S-wave interaction

doi:10.1088/1674-1056/abbbdb

中国物理B ›› 2020, Vol. 29 ›› Issue (11): 117201-.doi: 10.1088/1674-1056/abbbdb

Xun-Gao Wang(王勋高)¹^,², Huan-Yu Wang(王寰宇)¹^,², Jiang-Min Zhang(张江敏)³^,⁴, Wu-Ming Liu(刘伍明)¹^,²^,⁵^,†()

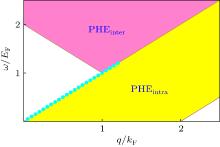
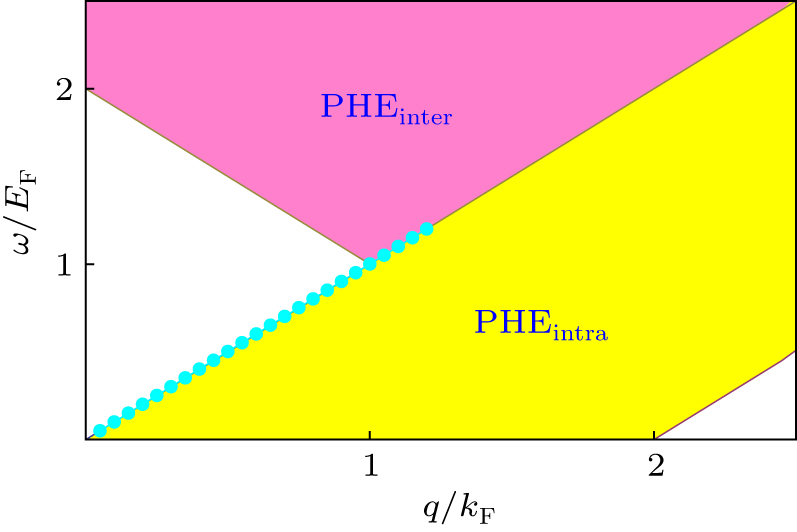
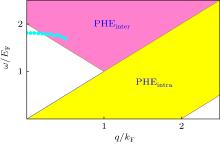
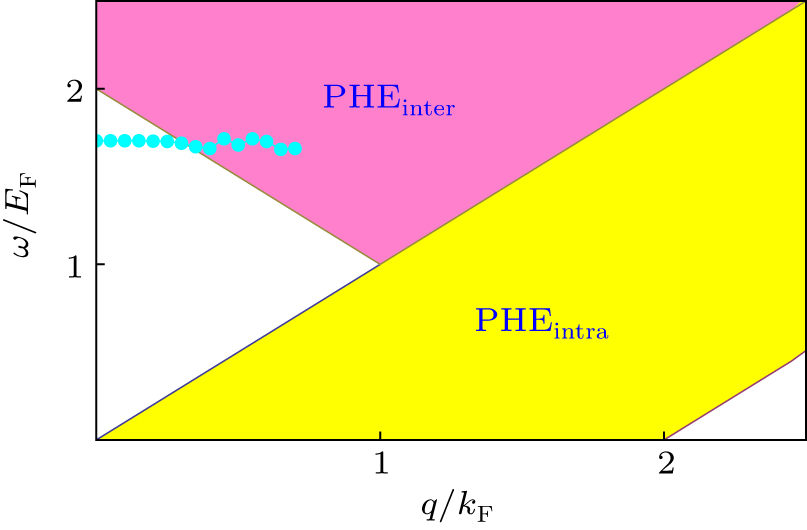
收稿日期:2020-08-27 修回日期:2020-09-11 接受日期:2020-09-28 出版日期:2020-11-05 发布日期:2020-11-03

Collective modes of Weyl fermions with repulsive S-wave interaction

Xun-Gao Wang(王勋高)^1,2, Huan-Yu Wang(王寰宇)^1,2, Jiang-Min Zhang(张江敏)^3,4, and Wu-Ming Liu(刘伍明)^{1,2,5, †}

1 Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
2 School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100190, China
3 Fujian Provincial Key Laboratory of Quantum Manipulation New Energy Materials College of Physics and Energy, Fujian Normal University, Fuzhou 350007, China
4 Fujian Provincial Collaborative Innovation Center for Optoelectronic Semiconductors and Efficient Devices, Xiamen 361005, China
5 Songshan Lake Materials Laboratory, Dongguan 523808, China

Received:2020-08-27 Revised:2020-09-11 Accepted:2020-09-28 Online:2020-11-05 Published:2020-11-03
Contact: ^†Corresponding author. E-mail: wliu@iphy.ac.cn
Supported by:
the National Natural Science Foundation of China (Grant No. 2016YFA0301500).

摘要/Abstract

Abstract:

We calculate the spin and density susceptibility of Weyl fermions with repulsive S-wave interaction in ultracold gases. Weyl fermions have a linear dispersion, which is qualitatively different from the parabolic dispersion of conventional materials. We find that there are different collective modes for the different strengths of repulsive interaction by solving the poles equations of the susceptibility in the random-phase approximation. In the long-wavelength limit, the sound velocity and the energy gaps vary with the different strengths of the interaction in the zero sound mode and the gapped modes, respectively. The particle–hole continuum is obtained as well, where the imaginary part of the susceptibility is nonzero.

Key words: ultracold gases, collective modes, random-phase approximation

Xun-Gao Wang(王勋高), Huan-Yu Wang(王寰宇), Jiang-Min Zhang(张江敏), Wu-Ming Liu(刘伍明). [J]. 中国物理B, 2020, 29(11): 117201-.

Xun-Gao Wang(王勋高), Huan-Yu Wang(王寰宇), Jiang-Min Zhang(张江敏), and Wu-Ming Liu(刘伍明). Collective modes of Weyl fermions with repulsive S-wave interaction[J]. Chin. Phys. B, 2020, 29(11): 117201-.

图/表 6

参考文献 25

[1]	Yang B J, Nagaosa N 2014 Nat. Commun. 5 4898 DOI: 10.1038/ncomms5898
[2]	Potter A C, Kimchi I, Vishwanath A 2014 Nat. Commun. 5 5161 DOI: 10.1038/ncomms6161
[3]	Rosenstein B, Shapiro B Y, Li D P, Shapiro I 2015 J. Phys.: Condens. Matter 27 025701 DOI: 10.1088/0953-8984/27/2/025701
[4]	Kung H H, Maiti S, Wang X, Cheong S W, Maslov D L, Blumberg G 2017 Phys. Rev. Lett. 119 136802 DOI: 10.1103/PhysRevLett.119.136802
[5]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 DOI: 10.1103/RevModPhys.82.3045
[6]	Wan X G, Turner A M, Vishwanath A, Savrasov S Y 2011 Phys. Rev. B 83 205101 DOI: 10.1103/PhysRevB.83.205101
[7]	Weng H M, Fang C, Fang Z, Bernevig B A, Dai X 2015 Phys. Rev. X 5 011029 DOI: 10.1103/PhysRevX.5.011029
[8]	Lv B Q, Weng H M, Fu B B, Wang X P, Miao H, Ma J, Richard P, Huang X C, Zhao L X, Chen G F, Fang Z, Dai X, Qian T, Ding H 2015 Phys. Rev. X 5 031013 DOI: 10.1103/PhysRevX.5.031013
[9]	Xu S Y, Belopolski I, Alidoust N et al. 2015 Science 349 613 DOI: 10.1126/science.aaa9297
[10]	Lu L, Wang Z Y, Ye D X, Ran L X, Fu L, Joannopoulos J D, Soljacic M 2015 Science 349 622 DOI: 10.1126/science.aaa9273
[11]	Dubcek T, Kennedy C, Lu L, Ketterle W, Soljacic M, Buljan H 2015 Phys. Rev. Lett. 114 225301 DOI: 10.1103/PhysRevLett.114.225301
[12]	He W Y, Zhang S Z, Law K T 2016 Phys. Rev. A 94 013606 DOI: 10.1103/PhysRevA.94.013606
[13]	Raghu S, Chung S B, Qi X L, Zhang S C 2010 Phys. Rev. Lett. 104 116401 DOI: 10.1103/PhysRevLett.104.116401
[14]	Sachdeva R, Thakur A, Vignale G, Agarwal 2015 Phys. Rev. B 91 205426 DOI: 10.1103/PhysRevB.91.205426
[15]	Srivatsa N S, Ganesh R 2018 Phys. Rev. B 98 165133 DOI: 10.1103/PhysRevB.98.165133
[16]	Gorbar E V, Miransky V A, Shovkovy I A, Sukhachov P O 2019 Phys. Rev. B 99 155120 DOI: 10.1103/PhysRevB.99.155120
[17]	Lv M, Zhang S C 2013 Int. J. Mod. Phys. B 25 1350177 DOI: 10.1142/S0217979213501774
[18]	Kohler T, Goral K, Julienne P S 2006 Rev. Mod. Phys. 78 1311 DOI: 10.1103/RevModPhys.78.1311
[19]	Chin C, Grimm R, Julienne P, Tiesinga E 2010 Rev. Mod. Phys. 82 1225 DOI: 10.1103/RevModPhys.82.1225
[20]	Zhang S S, Yu X L, Ye J W, Liu W M 2013 Phys. Rev. A 87 063623 DOI: 10.1103/PhysRevA.87.063623
[21]	Ryan J C 1991 Phys. Rev. B 43 4499 DOI: 10.1103/PhysRevB.43.4499
[22]	Maiti S, Zyuzin V, Maslov D L 2015 Phys. Rev. B 91 035106 DOI: 10.1103/PhysRevB.91.035106
[23]	Kumar A, Maslov D L 2017 Phys. Rev. B 95 165140 DOI: 10.1103/PhysRevB.95.165140
[24]	Mir M, Abedinpour S H 2017 Phys. Rev. B 96 245110 DOI: 10.1103/PhysRevB.96.245110
[25]	Principi A, Polini M, Vignale G 2009 Phys. Rev. B 80 075418 DOI: 10.1103/PhysRevB.80.075418

Collective modes of Weyl fermions with repulsive S-wave interaction

RichHTML

PDF (PC)

赞

可视化

摘要/Abstract

引用本文

使用本文

图/表 6

参考文献 25

相关文章 0

Metrics

本文评价

推荐阅读 0