† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51725104) and the Beijing Natural Science Foundation, China (Grant No. Z180009).
The critical properties and the nature of the ferromagnetic–paramagnetic phase transition in the 2D organic-inorganic hybrid (CH3NH3)2CuCl4 single crystal have been investigated by dc magnetization in the vicinity of the magnetic transition. Different techniques were used to estimate the critical exponents near the ferromagnetic–paramagnetic phase transition such as modified Arrott plots, the Kouvel–Fisher method, and the scaling hypothesis. Values of β = 0.22, γ = 0.82, and δ = 4.4 were obtained. These critical exponents are in line with their corresponding values confirmed through the scaling hypothesis as well as the Widom scaling relation, supporting their reliability. It is concluded that this 2D hybrid compound possesses strong ferromagnetic intra-layer exchange interaction as well as weak interlayer ferromagnetic coupling that causes a crossover from 2D to 3D long-range interaction.
Hybrid organic-inorganic compounds are an attractive family of materials in condensed matter physics, which have been extensively studied over the past decade for both fundamental science and technological applications.[1–5] Because of the combination of organic and inorganic moieties within a single structure, a variety of interesting properties have been discovered in these compounds.[6,7] In some organic-inorganic hybrids, the inorganic atoms are connected through covalent and ionic interactions to form the inorganic network. Meanwhile, the organic blocks can be connected by weaker interactions such as hydrogen and van der Waals bonding. Thus, a layered structure with quasi-two-dimensional magnetic interaction can be realized in them. Recently, two-dimensional (2D) magnetism has been a hot topic. It was previously thought that the surviving of long-range ferromagnetic (FM) order in 2D was hard due to increased fluctuation. However, the magnetic anisotropy in 2D magnetic crystals could stabilize the long-range magnetic order.[8]
To investigate the 2D magnetic phenomena, a critical exponent survey provides rich information. Accordingly, by evaluating the critical behavior, the nature of magnetic phase transition and inherent characteristics can be determined.[9]
Since the critical phenomena of magnetic organic-inorganic hybrids have not yet been well studied, in this paper, we performed a study on the critical behavior of a layer-structured organic-inorganic hybrid, (CH3NH3)2CuCl4. Various methods were used to estimate the critical exponents near the ferromagnetic–paramagnetic phase transition. A crossover from 2D to 3D long-range order was identified based on the analysis of the obtained critical exponents.
Single crystal samples of (CH3NH3)2CuCl4 were prepared via a solvothermal condition method as reported previously.[10] The structural properties of the samples were studied by x-ray diffraction using a Cu-Kα radiation source. Direct-current (dc) magnetization was measured by using a Quantum Design magnetic properties measurement system (MPMS) with the magnetic field applied parallel to the metal-halogen layers.
When a magnetic material undergoes a second-order phase transition, the critical behavior around Curie temperature TC can be characterized by a series of interrelated critical exponents, namely, β, γ, and δ.[11]
The magnetic equations can be given as



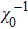
The parameter β (in the region below TC) is controlled by the temperature dependence of the spontaneous magnetization, and the parameter γ (in the region above TC) is controlled by the temperature dependence of the initial susceptibility. At TC, the δ exponent demonstrates the field dependence of the magnetization.
The scaling hypothesis provides another way to determine the critical exponents. The reduced magnetic equation of state that follows the critical region theory can be expressed as

The state described by the above equations will fall on two universal curves: one above TC and the other below TC. This is an important criterion for the critical regime; the exponents in the vicinity of TC confirm the universal properties.
Figure
 | Fig. 1. (a) The crystal structure of the 2D organic-inorganic hybrid compound. (b) Temperature dependence of FC magnetization with different applied magnetic fields in the ab plane. |
To determine the nature of the FM–PM phase transition, we plot the M2 vs. H/M curves in Fig.
In order to gain a deeper insight into the mechanism of magnetic interactions between the spins during the magnetic phase transition, the critical exponents need to be analyzed.[13] We use the modified Arrott plots (MAPs) method based on the Arrott–Noaks state equation to obtain the precise values of the critical exponents and the class of universality to which (CH3NH3)2CuCl4 could belong. The isotherm magnetization data is transmitted to a sequence of M1/β = f(μ0H/M)1/γ curves.
According to this method, the MAP is analyzed by certain types of possible exponents belonging to the triciritical mean-field model (β=0.25 and γ = 1), 3D-Heisenberg model (β = 0.365 and γ = 1.336), 3D-Ising model (β = 0.325 and γ = 1.24), and mean-field model (β = 0.5 and γ = 1), while the 2D-Ising model (β = 0.125 and γ = 1.75) is also considered,[11] which are shown in Figs.
| Table 1. Comparison of critical exponents of (CH3NH3)2CuCl4 obtained with different theoretical models: modified Arrott plot (MAP), Kouvel–Fisher (KF), critical isotherm analysis (CI). . |
The critical exponents for the above-mentioned models have been predicted by particular values. The mean-field model is suitable to describe the long-range magnetic interaction, which is equivalent to the classic Landau model. The tritical mean-filed model is used to explain the first-order and second-order magnetic interactions of the magnetic phase transition. 3D-Ising is appropriate for understanding the magnetic anisotropic uniaxial magnetocrystalline interaction[14] and 3D-Heisenberg is suitable for investigating the short-range magnetic interaction. The critical behavior is impressively influenced by the magnetization data in high magnetic field regions due to interplay variables such as charge, lattice, and orbital degree of freedom in a ferromagnetic system.[15] The lower-field data have not been considered in the fitting process, because they represent the arrangement of magnetic domains.[16]
As seen in Figs.
Figure
By following a standard procedure to identify the exact critical exponents β and γ, the linear extrapolation from the high-field straight line portions of the isotherms to the M1/β and (μ0H/M)1/γ axes provides the spontaneous magnetization MS(T,0) and the initial susceptibility 


Alternatively, the critical exponents and TC can be specified more accurately by the Kouvel–Fisher (KF) method based on the following equations:


As seen in Fig.
The third critical exponent δ can be calculated directly from the fitting of the critical isotherm M vs. H at TC (Fig.
 | Fig. 6. (a) Isothermal M(h) curve at TC. (b) The same plot on a log–log scale. The straight line is the linear fit of Eq. ( |
According to Wisdom’s scaling relation, the exponent δ can also be theoretically verified by the following relationship:

Since the obtained exponents of the sample are not matched with conventional universal classes, we investigate whether the acquired values of the critical exponents can generate the equation of the Widom’s scaling or not.[15,17]
The scaling analysis of Eq. (
Figure
 | Fig. 7. (a) Scaling plots of renormalized magnetization M| ε |−β vs. H| ε | −(β + γ) using β and γ determined by the KF method. (b) The alternative plot on a log–log scale. |
The Arrott–Noakes equation of state is


 | Fig. 8. (a) The (H/M)1/γ vs. (M)1/β curves with the critical exponents obtained from the KF method. (b) Temperature dependence of modified coefficients A′ and B′. |
The obtained critical exponents in the present study do not belong to any predicted class of universality. The effective critical exponents (βeff and γeff) have been examined as a function of ε using Eq. (

 | Fig. 9. Effective critical exponents (a) βeff and (b) γeff as a function of the reduced temperature ε. |
The origin of the FM interaction in this compound is due to the magnetic ions (Cu) in the ab plane and the antiferro distortive displacement of the halide ions within the ab plane, which is the consequence of Jahn–Teller distortion of the octahedral complex in the inorganic sheet. As a result, the single unpaired electron is located in the dx2–y2 orbital at each of the 3D holes of the Cu2+ ions in this compound, which aligns with the long axis of the octahedron and the spins experience FM superexchange, leading to a long-range FM order.[2,24–26]
It is clear from the previous sections that the FM interaction in this system does not completely conform to any predictive model. The results from the report of Taroni et al. show that the critical exponent β for the bidimensional system should be within the range 0.1 ≤ β ≤ 0.25.[26] The spontaneous survey magnetization by Jongh et al. illustrates that the critical exponent β is approximately 0.125 for the 2D system, except in the region very close to the ordering temperature; β will be changed to the 3D value of approximately 0.33 according to Griffiths universality hypothesis.[27] The β value of (CH3NH3)2CuCl4 is close to 0.25; this value lies between those of the 2D and 3D characteristics, which indicates that the interlayer coupling should be considerable. The exchange in the layer and between layers is typically strong and weak, respectively. Namely, the intralayer exchange is FM while the interlayer coupling is antiferromagnetic. For this sort of material including anisotropic intralayer exchange, a 2D-type behavior is predicted, but in a narrow ordering temperature (near TC), the crossover from 2D to 3D caused by the interlayer interaction begins to take effect.[28] The γ value is close to the mean-field model prediction and δ is located between the long-range and short-range couplings. These exponents can be attributed to a crossover effect of the 2D to the 3D system. To describe the crossover effect, we should consider the interlayer coupling.
The results indicate that the critical exponents in this compound do not strictly belong to the common universality models. Accordingly, it is important to determine the nature and the range of the interaction in the present study. For a homogeneous magnetic system, the universality of the magnetic phase transition is strongly dependent on the exchange interaction J(r). Renormalization group theory treats the magnetic ordering as an attractive interaction of spin which decays with distance r as


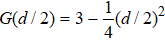
It has been argued that if σ ⩾ 2, the 3D-Heisenberg parameter is valid, where J(r) decreases faster than r−5. When σ ⩽ 3/2, the conditions for the mean-field model are satisfied so that J(r) decreases more slowly than r−4.5. In this research work, by using Eq. (
The previous study of the field dependent susceptibility demonstrated a very weak FM coupling near TC between the layers that causes the space dimensionality of the system to crossover to a 3D long-range order.[25] From the studies performed so far, it can be concluded that the strong magnetic anisotropy, as well as the dipole interaction and inevitable interlayer interaction, can induce the system to display a 3D long-range magnetic characteristic above TC.[29]
We have provided a detailed analysis on the critical exponents of the organic-inorganic hybrid with the formula (CH3NH3)2CuCl4. The system undergoes a second-order PM–FM phase transition. By using various methods, such as MAPs, Kouvel–Fisher, and critical isotherm analysis, the reliable critical exponents of β = 0.22, γ = 0.82, and δ = 4.4 were estimated. The critical exponents of this system do not belong to any universality class. The value of β is between those of the 2D and 3D systems and suggests a crossover from 2D to 3D near the Curie temperature.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |







