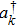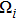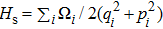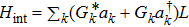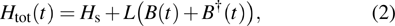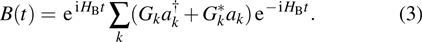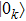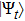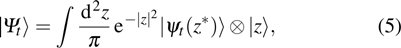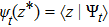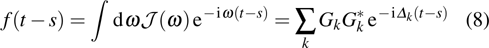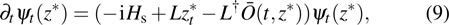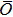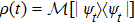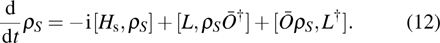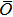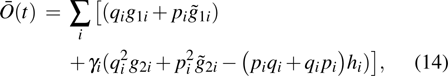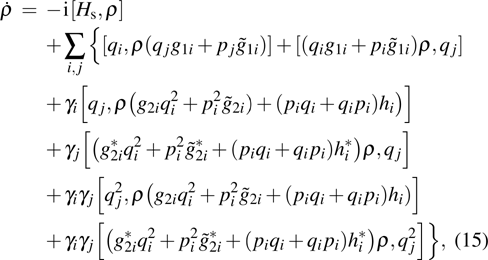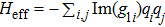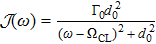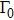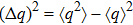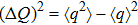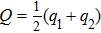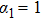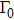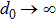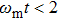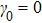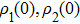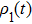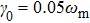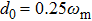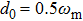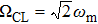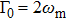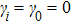Dynamics of two levitated nanospheres nonlinearly coupling with non-Markovian environment
School of Physics, Dalian University of Technology, Dalian 116026, China
† Corresponding author. E-mail:
jsjin@dlut.edu.cn zhlhxn@dlut.edu.cn
Project supported by the National Natural Science Foundation of China (Grant Nos. 11874099, 11605022, 11775040, 11747317, and 11474044).
1. IntroductionTrapping particles via an electromagnetic field is widely researched theoretically and experimentally because of its potential application in precise instrument and macroscopic quantum effects detection. For example, an optical tweezer is applied to capture and control cells in biological and medical research. The realization of Bose–Einstein condensation (BEC) and atom cooling have strict requirements for optical traps.[1–4] With the development of quantum techniques, the optical trap has been exploited in several research domains, such as generating squeezing states[5] and macroscopic superposition states of trapped matters,[6–8] entangling the trapped particles,[9,10] and cooling the trapped matter to ultra-low temperature.[11–14] In addition, the nonlinearity of the levitated system has been reported in Refs.[12–17]. The dynamics of a nanoparticle that nonlinearly couples to its reservoir has been theoretically studied in the Markovian regime.[18,19]
Non-Markovian theory plays an important role in treating a realistic system. The non-Markovian environment usually can keep the coherence and suppress the dissipation. The theory of open quantum system is researched through several perspectives, such as the projection operator theory,[20,21] Green's functions method,[22–24] perturbation theory,[25] and stochastic Schrödinger SSEs techniques.[26–30] However, these researches mostly investigate the system linearly coupling with its non-Markovian environment. However, the system coupled with its environment in nonlinear form remains under-studied.
In this paper we consider two nanospheres trapped by a continuous frequency field and we write the Hamiltonian of the system with a nonlinear coupling to its environment. By employing quantum state diffusion (QSD) method,[28–30] we derive a nonlinear master equation. We investigate the dynamics of the two levitated nanospheres with open quantum system techniques, and study the entanglement, squeezing of the two nanospheres, as well as the state transfer. We find that the nonlinear coupling can improve non-Markovianity.
2. Model and HamiltonianWe consider two nanospheres trapped by a wideband cavity. The wideband cavity field can be considered as a non-Markovian environment of the two levitated nanospheres. As found in Refs. [5] and [17], the vibration frequency of the trapped nanospheres is on the order of kHz or MHz, which is smaller than the width of the trapping field. This means that we can treat the trapping fields as a wideband cavity. Recently, the crystal cavity with engineering modes, whose frequency is continuous, has been employed for trapping nanoparticles.[31] When acted upon by the optical forces, named the gradient force Fgrad and the scattering force Fscatt, the two nanospheres can be described as harmonic oscillators that linearly and nonlinearly couple to the wideband cavity field (the detail illustration can be seen in Ref. [6]). The Hamiltonian can be written as
where
ak (
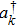
) is the annihilation (creation) operator of the
k-th mode with detuning
,
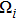
is the levitated frequency,
qi
is position (momentum) operator of the
i-th nanosphere, and
Gk is the coupling between the
k-th cavity field and nanospheres.
The Hamiltonian (1) describes the two nanospheres wrapped up by photon gas with a continuous spectrum distribution, which is analogous to Brownian motion. The system should be solved with non-Markovian theory. However, the third summation in Eq. (1) contains the nonlinear term in order of qi which differs from the usual linear non-Markovian interaction. The system can not be solved with the general non-Markovian theory as done in Refs. [23] and [32].
To treat the nonlinear and non-Markovian dynamics, we employ QSD method. For convenience, we rewrite the Hamiltonian into three parts, the free energy of the environment
, the energy of the two nanospheres
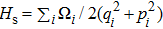, and the interaction part
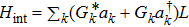, where
. It is convenient to change into the interaction picture rotating with HB, then we have the time-dependent Hamiltonian
with
The open quantum system obeys the non-Markovian quantum state diffusion equation
We assume the initial state of the system and environment as
. The system state
is arbitrary, and the initial states of the environment are their ground states
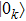
. The total state
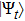
can be expanded as
where
, and
with identity for any Bargmann coherent state
The stochastic state of system
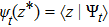
obeys QSD equation
where
is the correlation function of the bath. The variation in Eq. (
7) can be taken place by some time-dependent operator
O satisfying
. Therefore, the non-Markovian QSD equation (
7) is rewritten in a pseudo-time-local form
where
. The operators
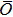
and
O satisfy
The reduced density operator of the open system can be obtained after partial trace operating over total state
, that is
We denote the reduced density operator
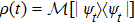
with operator ensemble mean
over all stochastic states. The master equation is obtained as
However, it is still difficult to find the exact solution of
O and
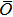
with Eq. (
10), especially when the system contains nonlinear or multi-particle interaction. An alternative method is to expand it in terms of the weak coupling strength, i.e.,
, where
G represents the coupling strength. The lowest order of this operator can be written as
by employing post-Markov approximation, which is valid when the square of the ratio of the environment memory time scale to system time scale is negligible.
[33,34] The integrated operator should be expressed as
where the coefficients can be found in Appendix B. From Eq. (
12), the master equation with nonlinear terms is obtained as
where
is the label of nonlinear coupling. The contributions of the linear and nonlinear couplings can be discussed by choosing
equal to zero or not. In addition, the method of the master equation deduction (
15) can be easily extended to that with nonlinear coupling. If the two nanospheres interact with other fields except the non-Markovian reservoir, then one only need to add their interaction into the Hamiltonian and perform the above procedure again.
3. Squeezing of levitated nanospheres induced by the wideband cavity fieldFrom the first line of the summation in Eq. (15), we can obtain an effective interaction between the two nanospheres resulting from the linear coupling, i.e.,
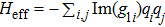, which can induce a self-squeezing and two-mode squeezing of the nanospheres.
Meanwhile, the nonlinear coupling between photon and phonon with
induces another effective interaction
which describes a Kerr effect.
We would like to investigate the effect of nonlinear coupling under Lorentz spectrum
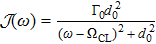, which is a typical example to analyze an open system thanks to its realism in experiment, where
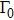is the spectrum strength and d0 is the spectrum width.
Squeezing can be quantified by the fluctuation of operators. The position fluctuation is defined as
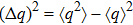. The two-mode fluctuation can be defined as
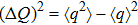, where
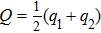. We choose
and assume that the initial states of the nanospheres are coherent states
with
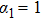and
. As shown in Fig. 1(a), the fluctuation
with linear coupling attains a relative “stable” value (with weak amplitude oscillation). When
, the single-mode squeezing finally disappears after long time evolution. For two-mode squeezing, there is little difference for
or not. Since the two-mode squeezing exhibits the correlation between the two nanospheres, the nonlinear coupling slightly affects the correlation. In addition, we can observe that the larger
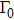, the stronger the two-mode squeezing, because
is the spectrum strength. The spectrum width d0 also has a little bit influence on the two-mode squeezing. One can see that the squeezing with
is stronger than that with
as shown in Fig. 1(b), but it does not mean the bigger d0 the stronger squeezing. In our simulation, we find that for
, there is no squeezing. If
,
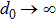, then it is Markovian and the squeezing is obviously worse than that of non-Markovian.
4. Entanglement and state transferThe two-mode squeezing represents the correlation between two nanospheres. Quantum entanglement, as an alternative correlation between two subsystems, can also be induced by effective interaction. The entanglement can be measured by negativity, which is defined as
where
is the minimum symplectic eigenvalue of 2 × 2 block covariance matrix
with element
(
) and
.
We plot the negativity in Fig. 2. The entanglement does not appear when
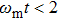then increases fast(sudden birth) and stabilizes without nonlinear coupling. When the nonlinear coupling is included, the entanglement is always less than that with
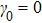, finally drops to zero, which means that the nonlinear coupling is not good for preserving the existence entanglement for a long time. This happens because the nonlinear coupling also induces an addition damping. We will explain this point later.
The effective interaction connects the two nanospheres, thus if the nanospheres are in different initial states
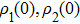, then the states
(
) will transfer to
(
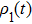) through effective interaction. We employ the conversion fidelity
to measure the efficiency of state transfer.[35] We plot the fidelity in Fig. 3. We can observe that the fidelity oscillates periodically with decreasing amplitude, whether or not the nonlinear coupling exists. When
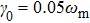, the fidelity is obviously worse than that with
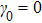. The maximum fidelity can reach 0.9, which is relative ideal, while the entanglement is weak (see Fig. 2) and the squeezing is not so deep (see Fig. 1). This happens because the equal frequency of the two nanospheres makes the effective interaction induced by linear coupling Heff with beam split (BS) form, therefore the state transfer can be achieved while the squeezing and the entanglement are not so ideal.
5. Non-Markovianity measureWe have shown that squeezing, entanglement, and state transfer between the two nanospheres can be achieved in our system. These properties result from their common coupling with the same non-Markovian environment; i.e., relating with the non-Markovianity in the present system. We now investigate the non-Markovianity of the system. For the non-Markovianity measure, several proposals[36–39] based on violation of dynamical semigroups or information backflow have been put forward. Here, we employ the measure of non-Markovianity proposed in Ref. [36]
where
is the derivative of trace distance between different initial states
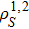
and
with
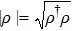
. Under this measure,
implies that the dynamical map
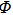
is non-Markovian. We calculate the non-Markovianity measure by solving Eq. (
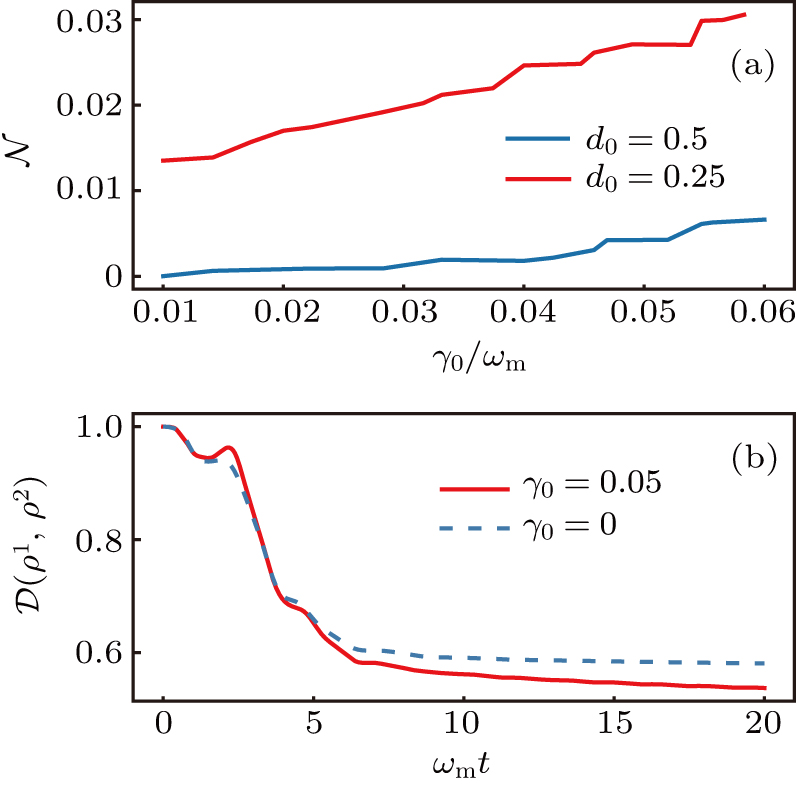
15). As shown in Fig.
4(a), with the increase of
, the non-Markovianity is improved whenever
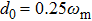
or
. Unfortunately, as we found in the previous section, the nonlinear coupling damages the squeezing, entanglement, and state transfer to some degree. This result conflicts with previous works, which declare that the information backflow could preserve those properties rather than damage them.
[40–43] To uncover the reason for this, we plot the trace distance between different initial states
in Fig.
4(b) with a random initial state pair where the initial state is the same for red and blue lines. After a long time evolution, the quasi-steady state may be achieved no matter what the initial state is. Therefore, the decline of
for different initial state indicates the dissipation of the system. As shown in Fig.
4(b), when
, a larger value of nonlinearity
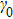
will lead to a faster decline of
, which means that a larger value of
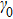
will lead to a larger dissipation rate. Thus, on the one hand the nonlinearity enhances the non-Markovianity, and on the other hand increases the loss rate. This is the reason why the squeezing and entanglement become bad after a long time evolution.
6. Discussion and conclusionWe investigate two nanospheres that are trapped in a wideband cavity field, where the two nanospheres nonlinearly couple with the environment. The main contribution of this work is that we put forward a method to treat non-Markovian dynamics with nonlinear coupling. A master equation of the nonlinear non-Markovian system is derived, in which the effective linear and nonlinear interactions can be induced, which can generate the squeezing, entanglement, and realize state transfer. We study the influence of this nonlinear coupling on the dynamics of the system. We find that the nonlinear coupling can improve non-Markovianity. After a long enough evolution, the nonlinear coupling will damage the squeezing and entanglement because the nonlinearity enlarges the loss rate. To compensate for the loss of the system, one can introduce another pumping field. In addition, one can see that the entanglement and the squeezing are not as good as the state transfer because the equal frequency of the two nanospheres results in the main interaction with beam split form. If one would like to obtain large entanglement and squeezing, then one could manipulate the two nanospheres with red and blue detunings, respectively. The spectrum of the environment depends on the distribution of the cavity field, which can be manipulated. Therefore, it might be a way to simulate the spectrum of the environment to study the non-Markovian system.
Acknowledgement
We would like to thank Xinyu Zhao and W. L. Li for helpful discussions.
