† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51590880) and the National Key Research and Development Program of China (Grant Nos. 2014CB643700 and 2016YFB070090).
The melt-spinning technique offers an opportunity for tailoring magnetic properties by controlling the structures and microstructures in both single-phase and composite magnets. This review first broadly discusses the principle of cooling control, amorphization, crystallization, annealing, and consolidation of the melt-spun ribbons. The phase, microstructure, and magnetic properties of popular single-phase nanocrystalline magnets are reviewed, followed by the nanocomposite magnets consisting of magnetically hard and soft phases. The precipitation-hardened magnetic materials prepared by melt spinning are also discussed. Finally, the role of intergrain exchange coupling, thermal fluctuation, and reversible/irreversible magnetization processes are discussed and correlated to the magnetic phenomena in both single-phase and nanocomposite magnets.
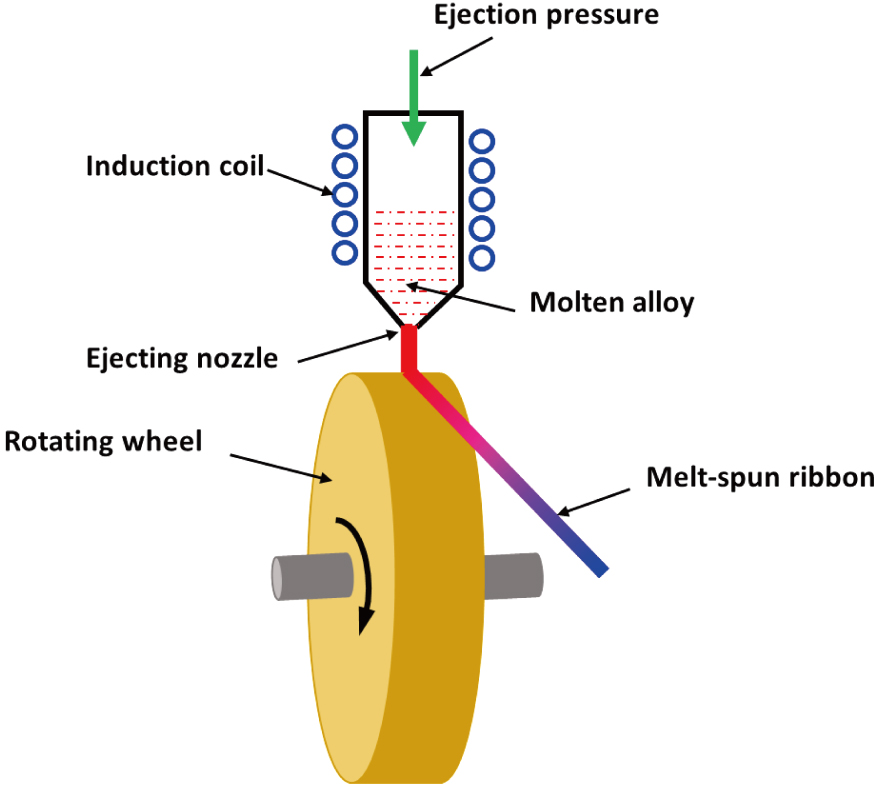
Melt spinning is a technique used for rapid cooling of molten liquids to produce metallic metastable solid solutions, which was introduced in 1960.[1,2] Both twin-roller and single-roller methods were introduced to produce rapidly solidified metallic ribbons, although the single-roller method is most widely used nowadays because of its simplicity and reproducibility. Figure
The melt-spinning technique is widely used to develop materials that require extremely high cooling rates in order to form metallic glasses or materials with extremely small grains or nanocrystals. The structure of final products formed by melt-spinning depends on the cooling rate, which can be described by continuous cooling transformation (CCT) curves.[3] Figure
 | Fig. 2. (color online) Schematic illustration of CCT behaviors in melt-spinning process. Tm is melting point; Tg is glass-transformation temperature.[3] |
The cooling rate of the melt-spinning process depends on the following factors: the thickness of the melt to be cooled, which is normally controlled by changing the revolution rate of the quenching roller; the pour rate of the molten alloy, which is normally controlled by the opening diameter of the ejecting nozzle and pressure; the heat transfer from the melt to the roller surface, which depends on interface energy between the melt and the roller surface, heat conductivity of the roller material, heat transfer between the roller and cooling water, and so on. After the rapidly quenched material leaves the rotating wheel, it is further cooled down by radiation and heat transfer to the surrounding gas, which is normally inert gas such as Ar or N2 for air-sensitive materials. Therefore, all the above factors need to be considered when the experiment is designed and performed during the melt spinning process.
The commercial and technological interests of melt spinning have been initially paid to soft amorphous and nanocrystalline magnetic materials prior to hard magnetic materials. The first ferromagnetic melt-quenched glassy alloys Pd12Co68Si20 were reported by Tsuei and Duwez.[4] The rapid quenched soft magnetic materials exhibit very low coercivity, which originates from the absence of magnetocrystalline anisotropy in these amorphous alloys.[5] Special attention has also been paid to the study of nanocrystalline phases obtained by suitable annealing of amorphous metallic ribbons. Such nanocrystalline magnetic materials exhibit excellent soft magnetic properties such as high saturated magnetization, high permeability, and low core loss simultaneously as the grain size below 10 nm, which was theoretically estimated by Herzer.[6] The melt-spinning technique is a great method to produce such nanocrystalline soft magnetic materials, and thus leads to the successful development of Fe–Cu–Nb–Si–B alloys (a trade name of “FINEMET”).[7]
The application of melt spinning on producing permanent magnets began on the demand of reducing the particle size of polycrystalline permanent magnetic materials, where their coercivity, Hc, is strongly dependent on the size of particles or grains. It is often agreed that the coercivity increases with decreasing particle size as it approaches the single domain particle size. The two common ways to decrease particle size or grain size are ball-milling and melt-spinning processes. The ball milling route seems very attractive since it is a simple process and it may produce single crystals which can be aligned by a magnetic field. Unfortunately, the conventional milling method cannot produce particles smaller than 
In addition to the superior of coercivity, the remanence is also enhanced in the isotropic nanocrystalline permanent magnet, which is known as remanence enhancement. Within the framework of the Stoner–Wohlfarth theory, the remanence is half of the saturated magnetization (Ms), i.e., Mr= Ms/2, or the normalized remanence Mr/Ms is 1/2, for an assembly of non-interacting and randomly oriented single domain particles.[10] However, the intergrain exchange interaction in nanocrystalline magnets, even in single-phase magnets, usually leads to a Mr/Ms larger than 1/2, i.e., remanence enhancement.[11] Numerical simulations show that a remanence could be enhanced by more than 40% as compared to the non-interacting particles if the grain size is in the order of 10–30 nm.[12]
The exchange interaction not only exists in single-phase nanocrystalline magnets, but also in nanocomposite magnets consisting of a magnetically hard phase such as Nd–Fe–B and a magnetically soft phase such as α-Fe. Actually, the inter-phase exchange interaction has bigger impacts on the remanence enhancement than the intergrain exchange interaction in single phase due to the low magnetocrystalline anisotropy of the magnetically soft phase. In the meantime, the inter-phase exchange interaction also prevents the reversal of the magnetic moments in the soft phase and thus retains a comparable coercivity to the original hard phase. This is the key idea of the nanocomposite permanent magnet which was proposed by Kneller and Hawig in 1991.[13] The theoretical prediction shows that the energy product of nanocomposite permanent magnet could be double compared to the theoretical limit of single-phase magnet.[14] Micromagnetic simulations confirm that the inter-phase exchange interaction could enhance the remanence with respect to non-interacting particles.[15–17] Extensive research has been devoted to this topic in the past 25 years for both experimental and numerical studies.
This article is organized as follows. Section
For melt-spun materials, there are many parameters to explore in order to achieve a certain magnetic phase and optimize the magnetic performance. First of all, the composition of the alloy is of major importance, not only considering the main elements Nd, Fe, and B, but also the additives, such as Nb, Al, Cu, etc. Secondly, there are many quenching parameters to be precise, which were mentioned in section 1.2. Thirdly, the ribbons obtained by melt spinning can be used directly or with subsequent heat treatment, such us post-annealing, hot pressing, or die upsetting. In the latter case, the pressure and temperature are critical and must be carefully controlled.
This section will discuss the unique characteristics of melt-spun materials using Nd–Fe–B as an example. Figure
The melt-spinning process is different from the conventional casting and sintering process. The super high cooling rate could prevent the eutectic crystallization and thus no residual α-Fe and Nd-rich grains in the quenched ribbons even in the stoichiometric Nd2Fe14B alloy. However, rapidly solidified Nd2Fe14B alloys may have different microstructural features depending on the thermal history of melt before ejection. To better understand the process of melt spinning, a CCT diagram is much better than the phase diagram since the phase diagram only indicates the equilibrium phases. Under no equilibrium conditions, kinetic as well as thermodynamic factors determine what phases and the microstructure will form. Although the development of quantitative CCT diagram is difficult for melt-spinning process due to the extremely high cooling rate, the qualitative representations of the process in Nd–Fe–B system are still possible and are conceptually useful. Branagan and McCallum developed such a CCT diagram in order to interpret the impact of cooling rate on the phase formation in the Nd2Fe14B system near stoichiometric 2:14:1 phase,[18,20] as shown in Fig.
 | Fig. 4. (color online) CCT diagram for stoichiometric Nd2Fe14B. Reproduced from Ref. [18]. |
Six representative cooling curves are drawn on the CCT diagram, starting from the ejection temperature (Te) of the melting spinning, which are summarized below.
For cooling curve A, the sufficiently high cooling rate makes it possible to form a 100% amorphous structure as the alloy is cooled below the glass transition temperature before crystalline phases can nucleate.
On the other hand, the cooling curve F on the right-hand of the diagram is near equilibrium cooling. Fe begins to precipitate at the liquidus. Once the peritectic temperature is reached, the Fe and the liquid react to form the 2:14:1 phase.
In the powder metallurgy route, solidification rates during casting occur between cooling curves D and E. The solidification sequence begins with the properitectic reaction and Fe formation (region 1), followed by the peritectic reaction (region 3) which requires bulk diffusion and is very sluggish. The cooling rates are fast enough in this region to allow only limited diffusion, which causes bulk segregation in both the liquid and solid phases. The solidification sequence after the peritectic reaction occurs through the hyperperitectic (region 4), proeutectic (region 5), and ternary eutectic reaction (region 6) as shown in Fig.
When the cooling rate is sufficient to undercool below the peritectic temperature, direct solidification of the 2:14:1 phase occurs. Cooling curve B gives a fully crystallized 2:14:1 single-phase microstructure, while cooling rate between A and B causes partially crystallization and represents an overquenched condition. The optimum cooling rate, which is slightly faster than cooling curve B, will generate the ideal microstructure consisting of an almost completely crystallized nanostructure and a small amount of amorphous grain boundary phase. The grain boundary amorphous phase is important for magnetically decouple adjacent grains, similar to the Nd-rich grain boundary in sintered magnets. The 2:14:1 phase content decreases with increasing cooling rate from B to A, while the amorphous content increases.[21]
In cooling curve C, a completely crystalline 2:14:1 structure can be formed but the alloy is in the under quenched condition. Therefore, the grains have time to grow above the optimum grain size during cooling.
The CCT diagram has been used to explain the effects of cooling rate and the alloy modifications on phase formation in 2:14:1 alloys through experiments by Branagan and McCallum.[18] A series of wheel speed (vws) from 5 to 30 m/s were controlled while other melt-spinning parameters are fixed same. The analysis shows that the cooling rate achieved in the 
Besides the cooling rate, the melting temperature prior to ejection, Te, also plays an important role on the microstructure of quenched ribbons. Tang et al. studied the impact of Te varying from 1300 °C to 1500 °C, as well as the cooling rate, on the phase formation of the stoichiometric 2:14:1 alloys through thermal analysis and transmission electron microscopy (TEM) analysis.[21] It was observed that a lower melt ejection temperature around 1300 °C produced a nanocrystalline microstructure, while higher melt ejection temperatures above 1450 °C largely eliminated the presence of nuclei and associated nanophases and thus produced an amorphous product. Therefore, an increase in the ejection temperature leads to a decrease in the wheel speed necessary to attain an optimum microstructure and thus energy product, as shown in Fig.
 | Fig. 5. (BH)max of as-spun ribbons produced under different ejection temperatures and wheel speed conditions.[21] |
Although directly quenching into nanocrystalline magnet has less processing steps, forming an amorphous or overquenched structure is easier to control for melt-spinning procedures. It also represents a wider processing zone for post-treatment after quenching. In thermomechanical processing, such as hot pressing, the overquenched materials allow more time for compaction to reach full density before the grains growth above the optimum size. Therefore, the overquenched approach is more popular than direct solidification into nanocrystalline. The glass-forming ability of alloys is then very important for this approach. Brangan et al. investigated the effects of Ti and/or C additions on the solidification behavior of Nd2Fe14B alloys.[18,23,24] They found that the glass-forming ability of the Ti/C added materials substantially increases, as the wheel speed drops from 30 m/s down to 12 m/s in order to form the amorphous. The addition of Ga based on the Nd–Fe–B–Ti–C alloy could further reduce the glass forming ability and refine the magnetically hard grains in the final materials.[25] Shen et al. found that a wheel speed of only 6.6 m/s could produce an amorphous structure in the rapidly quenched high B content Nd–Fe–B alloys.[26,27]
In addition to improving the glass forming ability of alloys, controlling the post-annealing condition is one of the key factors to optimize the microstructure and magnetic properties of the Nd2Fe14B ribbons. The annealing temperature is usually guided by the crystallization temperature of the amorphous, Tcr, which is typically determined by differential scanning calorimetry (DSC) curve, or differential thermal analysis CDTA curve. Figure
 | Fig. 6. DSC curves of amorphous Nd–Fe–B alloy showing the exothermic crystallization peak at 608 °C, where the onset temperature is 590 °C during the first heating. The second heating curve indicates the Curie temperature at Tc = 315 °C.[28] |
 | Fig. 7. (color online) Dependence of crystallization temperature of amorphous Ndy(Fe1−xBx)100−y alloys on B content with y = 4, 7, and 12.[27,31–34] |
A maximum crystallization temperature is observed in the Nd12Fe73B15, which is exactly the eutectic composition of the ternary Nd–Fe–B system. It is believed that a small amount of Nd addition into the Fe–B alloys leads to the increase of alloy viscosity and reduction of diffusion coefficient, and thus the enhancement of thermal stability of amorphous alloys. This is why the crystallization temperature of Nd–Fe–B is about 120–210 °C higher than that of Fe–B alloys.[31,35] The effects of other elements on the crystallization temperature have also been studied, with some of the results are summarized in Table
| Table 2. Impact of additives on crystallization temperature of Nd2Fe14B alloys. . |
The optimum annealing temperature for overquenched RE–Fe–B ribbons is slightly higher than the crystallization temperature, i.e., in the range of 650–800 °C, which leads to the formation of an optimum microstructure for magnetic hardening. Particularly, it eliminates α-Fe or Fe3B phase, which is usually the first product of the crystallization process. Gu et al. studied the crystallization and magnetic properties of amorphous NdxFe81B19−x alloys systematically.[41] Table
| Table 3. Phase components in annealed NdxFe81B19−x alloys.[41] . |
Besides annealing temperature, the annealing time affects the phase formation as well. A melt-spun amorphous exhibits formation of various phase as time elapses in isothermal annealing and are shown in Table
| Table 4. Crystalline phases in Nd4.5Fe77B18.5 during isothermal annealing.[3] . |
The crystallization also depends on the initial phase structure of the quenched ribbons. Men et al. prepared a set of ribbons with different initial phase structure, i.e., amorphous, TbCu7-type Nd2Fe17Bx, α-Fe, and their mixture, by varying wheel speed from 15 to 40 m/s.[43] They used the theory of energy barrier to interpret the crystallization process, as schematized in Fig.
 | Fig. 8. (color online) The crystallization mechanism of as-quenched ribbons with different initial phase structure. 




|
Most applications required a bulk-shaped permanent magnet, instead of ribbons, flakes or powders. Bulk nanostructured magnets can be produced through direct casting, compression molding, injecting molding, hot compaction, hot-deformation and other technologies. The direct casting process requires the remarkable glass-forming ability of the alloys in order to cast them into amorphous or nanocrystalline tubes or rods with 0.5–2 mm in diameter, followed by crystallization annealing to form the appropriate nanocrystalline structure and hard magnetic properties.[44–47] Although it is feasible to make bulk magnets through direct casting, the popular bulk nanostructured permanent magnets are still bonded magnets and hot-deformed magnets.
Bonded magnets can be manufactured by compression molding, extrusion, injection molding or calendering processes. In their most basic form bonded magnets consist of two components: a hard magnetic powder and a non-magnetic polymer or rubber binder.[48] For bonded magnets utilizing melt-spun products, the powders are general in a small flake shape such as the Magnequench powders. The binder that holds the magnetic particles in place can produce either a flexible or rigid magnet. Bonded magnets are usually isotropic due to the naturally isotropic grain structure of the melt-spun ribbons. However anisotropic bonded could be produced as well, if the texture is obtained in the melt-spun ribbons,[49] or if single crystal powders can be produced by special crashing methods.[50] The processes and magnetic properties of RE bonded magnets have been thoroughly reviewed by Liu and Walmer.[51]
Compression molding is the process which produces the best magnetic properties. The processed melt-spun powders are coated by a thin film of thermoset epoxy, hardener and other additives. The encapsulated powders are then fed into a press cavity and compacted under pressure, followed by curing at a temperature about 150–175 °C. One major advantage of compression bonding is that the volume of magnetic powders can be as high as 85%, resulting in a higher flux density than other methods. The maximum energy product of compression molded isotropic Nd–Fe–B magnets is about 10–12 MGOe. Injection molding is the process of injecting a molten, highly filled thermoplastic compound into mold cavities where it is allowed to cool and solidify. Both Nd–Fe–B, Sm–Co, and ferrite powders are commonly used as the magnetic powder in the compound. The injection molding process has the advantage of producing complex-shaped components with consistent accuracy. Typical magnetic powder volume is around 65%, with an energy product of about 5–6 MGOe for isotropic Nd–Fe–B bonded magnet. Extrusion and calendering are commonly used for flexible bonded ferrite magnets, while it may be used for melt-spun powders as well. The advantage of these processes is the continuous production of magnets of two-dimensional geometries, such as strips or sheets of virtually unlimited length with a typical sheet thickness of 0.3–6 mm.
While bonded magnets could be made from different magnetic powders, hot compaction is more suitable to nanocrystalline magnetic powders, especially for isotropic magnets. Hot compaction is a high-pressure, low-strain-rate powder metallurgy process for forming of powder compact at a temperature high enough to induce sintering or creeping processes. Within hot compaction technology, three distinctly different types of heating can be applied: inductive heating, indirect resistance heating, and direct heating. Among these three methods, inductive heating, where the heat is generated by using an induction coil, is rarely used for hot compaction of permanent magnetic materials.
With indirect resistance heating technology, the mold is placed in a heating chamber, which is powered by heating elements, as shown in Fig.
 | Fig. 9. (color online) Schematic of hot compaction through two different heating methods: (a) indirect resistance heating; (b) direct heating such as Joule-heating or SPS heating. |
For direct hot pressing, the mold is directly connected to electrical power. The resistivity of the mold and the powder part generates the heat directly in the mold, as shown in Fig.
Instead of using pulsed DC current in SPS technique, Rong et al. developed a similar but simplified hot press using AC current as a heating source, which could reach a heating rate of 300 °C/min. The fast heating benefits the controlling of grain size and nanostructure in the compaction processes, especially for the hard/soft nanocomposite magnets where the grain size of the magnetically soft phase is critically important. Another improvement of this instrument is the much higher pressure up to 2 GPa, comparing to the SPS press with graphite die.[60,61] The higher pressure could further lower the compaction temperature, which is in turn to prevent excessive grain growth. A maximum energy product of 18.5 MGOe is obtained in the fully dense SmCo5/α-Fe nanocrystalline magnet with magnetically soft grains of 8–15 nm by compaction at a temperature as low as 540 °C.[60]
The explosive or shock compaction is a technique of consolidating powders using high-pressure shock waves, which is considered as a potential method to consolidate hard-to-sinter powders and amorphous or fine nanocrystalline powders. Extremely high pressures up to 20 GPa can be applied to the powders in a very short time, even within several milliseconds.[62] The amorphous or nanocrystalline has no time to gain growth in such a short period. The shock compaction has been successfully used to produce bulk nanocrystalline permanent magnets in the past 20 years, including Nd2Fe14B,[63] Pr2Fe14B/α-Fe,[64] Sm–Fe–N,[65] and Fe16N2.[66]
Besides sintering technology, hot-deformation-induced texturing of nanocrystalline materials is another option for producing fully dense, anisotropic magnets with maximized energy products. Hot deformed Nd–Fe–B magnets have attracted attention not only because of their good magnetic properties but also due to their exceptional corrosion resistance, thermal stability, and fracture toughness compared to sintered magnets.[67] The hot deformation process usually starts from the preparation of a fully dense isotropic precursor. The precursor is then placed in an oversized die-cavity where die-upsetting is carried out at similar temperatures, as schematized in Fig.
 | Fig. 10. (color online) Schematic of hot deformation: (a) Die-upsetting; (b) backward extrusion; (c) typical microstructure of hot-deformed magnet.[61] |
Alternatively, backward extrusion can be utilized to produce near-net shape ring magnets, especially for small dimensions. Backward extrusion offers many advantages, including lower materials consumption, higher dimensional accuracy, and surface quality, adequate mechanical properties and the elimination of subsequent operations. The ring magnets produced by backward extrusion have superior magnetic properties to sintered magnets, which have been already used in electrified vehicles directly. Similar to die upsetting, a fully dense precursor need to be produced by hot compaction before backward extrusion, as schematized in Fig.
The single-phase magnetic materials usually have a chemical composition very close to the stoichiometric composition to minimize the presence of secondary phases. The nanostructure is obtained either by direct quenching into nanocrystalline through optimum melt-spinning parameters, or by crystallization of the precursor amorphous alloys formed through over quenching process. The single-phase magnets with different phase structure are reviewed below.
The 2:14:1 phase has a P42/mnm tetragonal space group with four formula units or 68 atoms per unit cell. Nd2Fe14B is the most common studied material with 2:14:1 phase structure. The microstructure of single-phase Nd2Fe14B melt-spun materials is fairly uniform, consisting of randomly oriented grains of the magnetically hard phase as shown in Fig. 
 | Fig. 11. (a) Typical microstructure of nanocrystalline Nd2Fe14B;[76] high-resolution TEM of (b) stoichiometric and (c) decoupled 2:14:1 magnets.[75] |
To achieve even higher coercivity in a permanent magnet, the magnetically hard grains need to be decoupled. Although an amorphous grain boundary can be formed by optimum the cooling conditions in the as-spun ribbons, most commercial alloys contain excess Nd. The resulting microstructure obtained by melt-spinning qualitatively agrees with the situation in sintered permanent magnets where the single crystallites of the magnetically hard phase are more or less magnetically decoupled by a paramagnetic RE-rich boundary phase. However, the scale of the melt-spun microstructure is about a factor of 100 smaller than sintered magnet and the easy axes of the nanograins are isotopically distributed instead of aligned. The high-resolution TEM micrograph in Fig.
If the alloy composition is chosen near to the two-phase line Fe–T1 on the left region bordering the stoichiometric T1 phase (as shown in Fig.
The Nd2Fe14B phase is the most widely studied permanent magnetic materials by melt spinning as well as other techniques due to the excellent magnetic properties, i.e., high anisotropy field (
(i) RE substitution for Nd
Replacing Nd by HRE such as Dy or Tb is an effective to raise the coercivity for higher temperature application since Dy2Fe14B and Tb2Fe14B have much higher anisotropy field comparing to Nd2Fe14B magnets, as seen in Table
Besides high-temperature application, element substitution is also useful for low-temperature application. For example, Pr2Fe14B magnets can be used at low temperature because there is no spin reorientation, while they have similar magnetic properties to those of Nd2Fe14B. Hadjipanayis et al. reported a coercivity of 2 T and energy product of 12 MGOe in the melt-spun single-phase Pr2Fe14B ribbons.[78]
Although RE elements are not truly rare geologically, they are expensive due to the extraction process, which makes the rare-earth magnets much more expensive than those of ferrite magnets. In order to reduce the material cost while utilize the still high magnetocrystalline structure of 2:14:1 phase, La/Ce based RE2Fe14B magnets attract the interests recently. Significant cost reduction can be achieved due to the much cheaper price of La/Ce by slightly sacrificing magnetic properties. An energy product of 8.6 MGOe is achieved in the Ce–Fe–B melt-spun ribbons as reported by Zhou et al.[79] If Nd is only half replaced by Ce, the energy product of 14.3 MGOe can be obtained through melt spinning as reported by Li et al.[80] The magnetic properties of the Ce-substituted Nd2Fe14B ribbons are summarized in Table
| Table 6. Magnetic properties of melt-spun Nd12−xCexFe82B6 ribbons.[80] . |
(ii) Co substitution for Fe
Replacing Fe by Co substitution is an effective way to raise Curie temperature and potentially reduces temperature coefficients of coercivity and remanence. It is known that Nd2(CoxFe1−x)14B pseudo-ternary systems form the 2:14:1-type crystal structure for all levels of cobalt substitution, with Tc increasing monotonically to ∼722 °C for Nd2Co14B.[87] It is found that the desirable enhancement of Tc is accompanied by improved temperature stability of the remanence in the Nd2(CoxFe1−x)14B melt-spun ribbons if the Co content is less than 30%.[88] However, the coercivity deteriorates dramatically as the Co content increases above 40% due to the easy formation of Nd2Co17 rather than Nd2Co14B. By systematically varying the composition of Nd–Co–B alloys, Fuerst and Herbst successfully developed melt-spun Nd2Co14B ribbons with a coercivity of 1.02 T and energy product of 5.2 MGOe.[89] The authors also fabricated the ribbons comprised principally of Pr2Co14B with a coercivity of 2.5 T and energy product of 5.5 MGOe.[90] It should be mentioned that RE2Co14B compounds do not form for all rare earths but only for R = Y, La, Pr, Nd, Sm, Gd, and Tb. Unfortunately, none of them has attracted much attention due to their unsatisfied properties for permanent magnetic applications. In advanced Nd–Fe–B permanent magnets, Fe is only partially substituted by Co.
(iii) C substitution for B
The magnetic properties of the carbide and boride 2:14:1 compounds are almost same. Typically, carbides have slightly lower Curie temperatures and saturation magnetizations, slightly higher magnetocrystalline anisotropies, as shown in Table
(iv) Other additives
With no substantial cost increase, researchers found that the magnetic properties are improved by means of small amounts of additives in the 2:14:1 base materials. The most common additives are Ti, V, Cr, Mn, Co, Ni, Cu, Zr, Nb, Mo, Ru, W, Al, Ga, Si, etc. According to the summary in Ref. [83], the additions of Co, Ni, Cu, Ga, and Si increase the Curie temperature, while the additions of Nb, Al, and Si increase the magnetocrystalline anisotropy of Nd2Fe14B phase. More importantly, the additives can modify the microstructure in order to achieve desirable magnetic properties. For example, Herbst et al. found that the addition of 0.5 at.% Cu enhances the intrinsic coercivity as much as 30% over that of Cu-free materials, which is attributed to the Cu preferential segregation in the intergranular regions.[95] El-Moneim et al. observed that partial substitution of Fe with Co and Ga leads to an improvement in corrosion resistance.[96] Chen et al. found that a small substitution of Nb for Fe results in an uniform microstructure with average grain size of only 10–20 nm, which is much smaller than the Nb-free ribbons.[97]
It should be emphasized again that the melt-spun materials based on 2:14:1 phase are typically isotropic which limits the maximum achievable energy products far lower than the theoretical value given in Table
The CaCu5-type 1:5 phase can be formed in the RE–Co and RE–Ni compounds with the composition of RE(Co, Ni)5. However, the highest Curie temperature of −240 °C is found in the RENi5 series for GdNi5, which makes them not practical for permanent magnet applications. On the other hand, Curie temperatures of most RECo5 compounds are higher than 500 °C, as shown in Table
| Table 7. Intrinsic magnetic properties and theoretical (BH)max limits of 1:5, 2:17 and other phases.[19,98,99] . |
Among RECo5 compounds, SmCo5 compounds are obvious candidates for developing coercivity, owing to their extraordinary magnetocrystalline anisotropy. However, the CaCu5-type 1:5 phase is stable only at temperature above 805 °C according to Sm–Co phase diagram,[100] below which it decomposes into Sm2Co7 and Sm2Co17 phases. The magnetocrystalline anisotropies of the 2:7 and 2:17 phases (∼20 T and ∼6–11 T, respectively) are less than that of 1:5 phase (25–44 T). In addition, the 2:7 phase can act as nucleation site of reversing domain wall, which decreases the coercivity of the SmCo5 magnets. Therefore, fast cooling rate is necessary to obtain a pure single phase SmCo5 magnet by suppressing the formation of the 2:7 and 2:17 phases, which makes the melt-spinning technique very suitable to fabricate the 1:5-type magnets.
Takahashi et al. prepared the melt-spun SmCo5 ribbons in 1985,[101] where they found that the columnar structure with c-axis aligned parallel to the ejecting direction of the ribbons at relatively low wheel speed below 18 m/s. This is the so-called preferred crystallographic orientation or texture. In the ribbons fabricated at higher wheel speed, only homogenous spherical fine particles with random orientation of c-axis were observed. Since the Co-rich part of the Sm–Co phase diagram does not have a deep eutectic, the melt spinning does not lead to an amorphous structure or even a very fine crystallized microstructure, which is the requirement for high coercivity. The coarse microstructure in typical Sm–Co melt-spun ribbons leads to a coercivity lower than that expected for a material with such a large anisotropy field. Therefore, it understandable that the above work only achieves a coercivity up to 1.5 T,[101] which is even lower than of the melt-spun Nd2Fe14B ribbons, although SmCo5 has much higher magnetocrystalline anisotropy. Ding et al. optimized the melt spinning process for SmCo5 ribbons and confirmed the dendritic structure with needle-like crystallites aligning preferentially in the ribbon plane in the low-speed prepared ribbons (vws 

Between the texture and the coercivity of melt-spun SmCo5 ribbons, texture attracts more attention due to the demand of higher energy products. Therefore, most of the recent efforts were focused on solidification at relatively low speeds. Actually, Ding et al. reported an energy product of 18 MGOe in the SmCo5 ribbons prepared at wheel speed of 6 m/s.[102] Yan et al. also reported the formation of crystallographic texture during melt-spinning process using low wheel speed.[104] The degree of the preferential alignment decreases at high wheel speed, while the ribbons prepared at 
 | Fig. 13. XRD patterns of SmCo5 ribbons prepared at (a) 5 m/s and (b) 25 m/s.[104] |
The element substitutions in SmCo5 ribbons influence both the microstructure and magnetic properties. Zhang et al. reported that Gd substation of Sm could effectively suppresses the formation of 2:7 phase,[106] which usually exists in the anisotropic SmCo5 ribbons without element substitution.[107] The improved microstructure leads to the increase of both coercivity and squareness of the M–H curve significantly. A high remanence ratio of 0.95 has been attained in Sm0.5Gd0.5Co5 ribbon with an energy product of 16 MGOe at room temperature. In addition, the temperature coefficient of remanence increases from −0.09% per °C for SmCo5 to +0.02% per °C for Sm0.5Gd0.5Co5 ribbons. This behavior could be attributed to the ferromagnetic coupling between HRE and Co atoms, which results in an increase of magnetization with increasing temperature in a given temperature range.
Enhanced saturated magnetization can be expected through Fe substation to Co, as Fe has larger magnetic moment than Co. Tung et al. found that Ms of as-spun SmCo5 ribbons is only 0.42 T, while that of as-spun SmCo3Fe2 ribbons is 1.20 T.[108] This huge enhancement cannot be only attributed the large magnetic moment of Fe. The TEM and energy dispersive analysis (EDX) analyses shows that a large portion of SmCo3 grain exists in the SmCo5 ribbons, which leads to low saturated magnetization in the ribbons. For the SmCo3Fe2 ribbons, the majority phase is Sm(Co, Fe)5 with a small portion of Sm2(Co, Fe)7 and Sm(Co, Fe)3 phases at the grain boundaries. In addition, XRD suggests the existence of α-Fe(Co) grains although it is not detected by TEM. Combining the grain refinement induced by the Fe substitution, a coercivity of 0.82 T and an energy product of 16 MGOe are obtained in the as-spun Sm(CoFe)5 ribbons without post-annealing.
The nonmagnetic element substitution for Co has also been studied in the SmCo5 ribbons. Yan et al. studied the effects of Cu and Sm doping on the magnetic properties of the oriented melt-spun ribbons with composition Sm1+y(Co1−xCux5, fabricated with a wheel speed of 5 m/s, followed by an optimized post-annealing.[109,110] The room temperature coercivity is significantly enhanced to 2.1 and 1.24 T by Sm additions and Cu substitution, respectively. Interestingly, it is found that the coercivity mechanism of the Sm-doped and Cu-substituted ribbons are completely different, i.e., the Sm-doped ribbon has a nucleation-type while Cu-substituted ribbon has a domain-wall pinning type coercivity mechanism. In addition, compared with the Sm-doped ribbons, Cu-doped ribbons exhibit a better thermal stability of coercivity and a high coercivity of 0.52 T even at 300 °C. Fukuzaki et al. investigated the effect of nonmagnetic element M (M=Zr), V, Nb, Mo, and Ta) substitutions on magnetic properties and microstructure of Sm(Co0.7Cu0.3)5Fe0.54−xMx ribbons.[111] It is observed that the coercivity increases initially with increasing the substitution content, reaches a maximum value at x = 0.2–0.3, and then decreases for all studied element except Zr, as shown in Fig.
 | Fig. 14. Coercivity of Sm(Co0.7Cu0.3)5Fe0.54−xMx (M = Zr, Nb, Mo, Ta) ribbons as a function of substitution element content.[111] |
Boron substitution of Co not only promotes amorphization in rapidly solidified Sm–Co alloys but also the formation of Sm–Co boride structures. The SmCo4B compound, in which the B atoms replacing Co in the parent SmCo5 structure, has a magnetocrystalline anisotropy even higher than SmCo5.[19] This makes SmCo4B a promising candidate for nanocrystalline hard magnet.
Unfortunately, the Curie temperature of SmCo4B is far lower than that of SmCo5. Two methods are utilized in order to improve the Curie temperature. Saito et al. found that melt spinning can stabilize the disordered SmCo5−xBx structure even with 
Hexagonal PrCo5 has comparable anisotropy field and saturated magnetization to those of SmCo5, as shown in Table
 | Fig. 15. (color online) TEM images of nanocrystalline PrCo5 prepared at (a) 30 m/s, (b) 70 m/s, and statistical grain size distribution of (c) 30 m/s, (d) 70 m/s.[116] |
It is interesting to know that the texture could be developed through die-upsetting method for the PrCo5 ribbons, which is similar to that of the Nd–Fe–B ribbons through plastic hot deformation procedure. Fuerst and Brewer observed this behavior in both Pr–Co and Pr–Co–C nanocrystalline ribbons with PrCo5 as the major phase.[117,118] Although the texture is not as perfect as that in Nd–Fe–B magnets, it induces marked increase of remanence. The greatest alignment was obtained in the die-upset magnets with low-carbon compositions; in particular, Pr18Co81C produced a remanence of 0.87 T and an energy product of 16.9 MGOe.[117] Through further partially substituting Sm with Pr, coercivities near ∼2.0 T were achieved in thermally quenched die-upset (Pr0.6Sm0.4)18Co81C magnets, while maintaining remanences above 0.8 T.[118] However, for unknown reasons, the Sm–Co alloys with much higher coercivity do not develop texture during die upsetting.
1:7-type RECo7 is a metastable phase in the RE–Co binary systems such as Sm–Co and Pr–Co. It has a TbCu7 crystal structure which can be derived from RECo5 when RE atoms are randomly substituted by Co pairs, confirmed by TEM study performed by Yu et al.[119] It should be noted that RE2Co17 can also have the 1:7-type structure when they are prepared appropriately. A third doping element such as Ti, Zr, Cu, is helpful to stabilize the 1:7-type phase if they are used to substitute Co. Among the 1:7-type RE–Co alloys, SmCo7 is the most studied materials. The SmCo7 compound has saturation magnetization and Curie temperature lower than a Sm2Co17 but higher than a SmCo5 compound. The anisotropy field of TbCu7-type Sm–Co alloys is reported to be 10.5–14.0 T, which is about more than 1.6 times of the Sm2Co17 phase.[120] In fact, the metastable SmCo7 phase can be obtained by various methods, such as arc melting,[121] mechanical alloying,[122] and melt spinning which is summarized here.
Various additions were tried to stabilize the 1:7 phase and refine the microstructure of SmCo7 ribbons. Guo et al. investigated the effect of transition metals (TM), such as Nb, Ta, Cr, and Mo, on the crystal structure and magnetic properties of melt-spun SmCo7−xTMx.[123,124] It was found that a pure TbCu7-type structure is formed in the SmCo7−xNbx and SmCo7−xTax ribbons, while minor amount of impurity 2:17 phase appears for the that of Cr or Mo substituted ribbons, implying that the elements in VIB group (Cr and Mo) are inferior to the element in VB group (Nb and Ta) in stabilizing metastable 1:7 phase. The impact of phase impurity is also reflected by the coercivity in the TM-substituted ribbons. The Nb/Ta substitution leads to the coercivity enhancement of 0.83–0.94 T, while Cr/Mo only leads to an enhancement of 0.47–0.56 T. The effect of Si and Al substitution in SmCo7 alloys has been investigated but the coercivity enhancement is much lower than that of Nb, Ta, Cr, and Mo.[125] Recent study shows that the coercivity can be highly enhanced in the SmCo7−xZrx ribbons only if the wheel speed is high enough. Particularly, a high coercivity of 1.72 T is achieved in the SmCo6.7Zr0.3 ribbon with a fine grain structure around 
Carbon in combination with some transition metal element can produce fine 1:7 microstructures with further enhancement of coercivity. Du et al. found that carbon addition helps the formation of homogeneous microstructure with grain size around 60–70 nm in the Sm(Co0.9Fe0.16.8Zr0.2Cx ribbons, which results in a coercivity of 1.43 T and an energy product of 11 MGOe.[127] With an optimized Fe content, the energy product is improved to 13.7 MGOe in the Sm(Co0.75Fe0.256.7Zr0.3C0.06 ribbon, while coercivity is slightly dropped.[128] Similar grain refinement and coercivity enhancement are observed in the NbC-doped ribbons as reported by Hsiao et al., confirming the role of carbon in the melt-spun 1:7-type alloys.[129] In fact, Li et al. found that the grain size of the melt-spun SmCo7−x(Cr3C2x ribbons decreases with the increase of Cr3C2 content.[130] The amorphous state is achieved in the ribbons with 
Alternatively, boron can be doped into 1:7-type ribbons and significantly improves the coercivity. Makridis et al. reported that the as-spun Sm(Co0.74−xFe0.1Cu0.12Zr0.04Bx7.5 ribbons contains mainly TbCu7-type phase with an average grain size of 60–100 nm.[131] A record high coercivity of 3.85 T at room temperature is achieved in these ribbons. It should be noted that excessive amount of B may lead to deterioration of the hard-magnetic properties. Kim et al. found that the magnetically soft Sm2Fe14B phase with a planar anisotropy can be formed in the Sm2(CoFeMn)17Bx ribbons if B is over-doped.[132]
TbCu7 structure is observed in the Pr–Co alloys as well. Zhang et al. reported the stabilized 1:7 phase in both compound through arc melting[133] and nanocrystalline powders with an average grain size of 20 nm through mechanical alloying of PrCo7−xTix alloys with an energy product of 10.6 MGOe.[134] With the assistance of C addition, Kostogorova et al. successfully fabricated the (PrxCo1−x94Ti3C3 ribbons consisting of 1:7 phase with a coercivity around 1.0 T through melt spinning and post-annealing.[135]
Besides microstructure refinement, the improvement of crystallographic texture in the melt-spun ribbons is also an effective way to promote the properties of 1:7-type magnets. Yan et al. observed a high degree of texture in the melt-spun Sm(CoFeCuZr)7.4 ribbons prepared at low wheel speed such as 5 m/s.[136] The formation of the crystallographic texture, with c-axis parallel to the longitudinal direction of ribbon, is attributed to a directional solidification process resulting from a temperature gradient. Maximum energy product of 12.3 MGOe is obtained in such highly-textured ribbons. Yan et al. also found that the C addition to Sm(CoZr)7 alloy not only significantly enhances the coercivity of the ribbons but also affects the crystallographic texture. The preferred orientation changes from parallel to the ribbon plane for carbon-free ribbon, to normal to the ribbon plane for the SmCo6.5Zr0.5C0.5 ribbon.[137] Figure
 | Fig. 16. SEM micrographs on the surface of (a) SmCo6.5Zr0.5 and (b) SmCo6.5Zr0.5C0.5 ribbons.[137] |
Since the Sm2Co17 and especially Sm2(CoFe)17 have saturated magnetization substantially higher than that of SmCo5, it seems natural to increase (BH)max in the Sm2Co17 magnets. Another advantage of Sm2Co17 is the higher Curie temperature compared to SmCo5 phase, as seen in Table
Sm2Fe17 compound has high saturation magnetization but shows low Curie temperature and planar anisotropy likely due to the strong Fe sublattice anisotropy. However, interstitial modification of the Sm2Fe17 compounds can leads to uniaxial anisotropy and dramatically change their magnetic properties.[99,141] Owing to a volume expansion of the atomic lattice caused by the absorbed N, C, or H atoms, the Curie temperature increases by more than 300 °C. In addition, both magnetocrystalline anisotropy and saturation magnetization also increase significantly, as shown in Table
Pinkerton and Fuerst obtained magnetically hard Sm–Fe–N ribbons with a room-temperature coercivity of 2.3 T by nitriding melt-spun Sm–Fe precursor ribbons. To facilitate the absorption of nitrogen, the ribbons were ground to powder with particle size less than 
Shield et al. found that melt spinning of the Sm11Fe89 alloys usually results in grain sizes at or above the single domain limit which is around 360 nm.[145] The addition of Ti and C leads to an order of magnitude refinement at the microstructural scale, resulting in the coercivity enhancement in the Sm2Fe17Nx ribbons. Omatsuzawa et al. investigated the isotropic TbCu7-type Sm–Zr–Fe–Co–N materials prepared by the melt spinning and following nitrogenation.[146] They found that the grain size decreased monotonically with the increase of the wheel speed, which leads to the increase of both remanence and coercivity. A compression-molded bonded magnet using the melt-spun powders at a wheel speed of 40 m/s showed excellent magnetically hard properties: μ0Mr = 0.83 T, μ0Hc = 0.9 T, and (BH)max = 14.2 MGOe. Even better properties were reported in the (Sm0.7Zr0.3)(Fe0.8Co0.2)9B0.1Nx ribbons with a single-phase TbCu7-type structure: μ0Mr = 1.07 T, μ0Hc = 0.98 T, and (BH)max = 22.6 MGOe.
The effect of interstitial carbon on Sm2Fe17 is similar to that of nitrogen. However, the number of the C atoms per formula unit after a solid–gas carburization usually does not exceed 2. This means a lesser volume expansion of the 2:17 lattice and thus lesser gain in the magnetic properties. As one can see in Table
Shen and his group have systematically studied the structure and magnetic properties of the RE2Fe17Cx (RE=Dy, Er, Ho, Er, Ge, Tm, Y) ribbons prepared by melt spinning and other approaches.[147–157] The Curie temperatures of RE2Fe17Cx are summarized in Fig.
 | Fig. 17. (a) Curie temperatures of R2Fe17Cx ribbons (x = 0, 1.0, 1.5, and 2.0); (b) Curie temperatures versus unit cell volume of Er2Fe17Cx and Tm2Fe17Cx; (c) dependence of Ms on carbon content of R2Fe17Cx ribbons.[147–157] |
Among all RE2Fe17Cx alloys, Sm2Fe17Cx is the best candidate for permanent magnets due to their high saturation magnetization and relatively high Curie temperature. It was found later by Shen et al. that substituting Fe partially with Ga, Al, Si, or Cr in Sm2Fe17Cx helps the formation of Sm–Fe compounds of even higher carbon content with the 2:17-type structure.[159–161] The excellent magnetic properties of these 2:17-type carbides results from not only the interstitial carbon atoms but also the substitutional Ga, Al, or Si atoms, which leads to a significant increase in the uniaxial anisotropy field.
Figure 
 | Fig. 18. Effect of carbon addition on (a) Tc, (b) HA, and (c) Ms of Sm2Fe17Cx and Sm2Fe15M2Cx alloys.[161–163] |
With an optimized carbon content, Shen and his group further optimized the Ga, Al, and Si substitutions on intrinsic magnetic properties of Sm2Fe15MxC1.0-1.5 alloys,[164,165] as shown in Fig. 
 | Fig. 19. The effect of Ga, Si, and Al substitutions on (a) Curie temperature, (b) anisotropy field, and (c) saturated magnetization of Sm2Fe15MxC1.0−1.5 alloys.[172,173] |
Compared with Sm2Fe17Cx, the further advantage of Sm2Fe15M2C materials is the developed coercivity and energy products. Zhang et al. studied the effects of wheel speed of melt spinning as well as the carbon content on the coercivity of the Sm2Fe14.5Cu0.5Ga2Cx ribbons,[174] as shown in Fig.
 | Fig. 20. (color online) Dependence of coercivity on wheel speed of Sm2Fe15−xCuxGa2Cx (x = 0–2.0) and Sm2Fe15Ga2C ribbons.[174] |
Sm(Fe, M)12 (M = Ti, V, Mo, Si) compounds with the tetragonal ThMn12 structure possess a uniaxial anisotropy at room temperature, which is large enough for the development of permanent magnet materials. Both melt spinning and ball milling were utilized to produce nanocrystalline Sm(Fe, M)12 magnets. The SmFe12−xMx magnets with the desired 1:12 structure can be obtained if 

Interstitial modification of the Nd(Fe, M)12 compounds changes their intrinsic magnetic properties in a way very similar to that of Sm2Fe17. The room-temperature coercivity of about 0.6–0.9 T are obtained by nitriding the melt-spun Nd(Fe, Mo)12 ribbons which only have coercivity less than 0.05 T prior to nitriding.[181] The magnetic properties and interstitial atom effects in the R(Fe, M)12 compounds have been reviewed in Ref. [182].
R3(Fe, Ti)29 is a novel intermetallic which crystallizes into a monoclinic structure with a space group of A2/m. The unit cell can be described as an alternate stacking of the tetragonal ThMn12-type and the rhombohedral Th2Zn17-type structures. There is a strong enhancement in saturated magnetization and Curie temperature (
Nd5Fe17 phase was found to be a stable intermetallic compound with a hexagonal structure in the binary Nd–Fe system. Although the Nd5Fe17 phase has a high saturated magnetization of 1.52 T at 4 K and a Curie temperature of 230 °C, it does not possess c-axis anisotropic, which is essential for permanent magnet materials. On the other hand, Sm5Fe17 phase is a metastable phase with a Curie temperature around 280 °C and an anisotropy field 
Recent constraints on availability and cost increase of RE elements have stimulated a strong interest in the discovery of RE-free materials with excellent permanent-magnet properties. Many RE-free candidates with high magnetic anisotropy and high Curie temperature have been proposed and studied in the past years. Here we only briefly reviewed some of them such as MnBi, Co-rich Hf–Co/Zr–Co, Fe–Pt–B, Mn–Al–C and Alnico, which are prepared by melt spinning.
The low temperature phase (LTP) MnBi compound is of interest not only because of its RE-free feature, but also because of its magnetic properties. The magnetic anisotropy constant of MnBi is negative below −170 °C but increases with increasing temperature and attains its maximum value of 2.2 × 106 J/m3 at 220 °C. Actually, the high temperature anisotropy constant of MnBi is much higher than that of Nd2Fe14B phase, although its room temperature value is lower. This made MnBi a good candidate for high temperature applications. However, the maximum energy product of MnBi at room temperature is much lower than most other permanent magnet materials, due to its low saturated magnetization. Guo et al. prepared the LTP MnBi by melt spinning and found a maximum anisotropy field of about 9 T at 257 °C and a Curie temperature of about 500 °C.[188] Following the above method, Saha et al. produced the MnBi powders with a coercivity of about 2.6 T at 280 °C by a ball milling process following the melt-spinning.[189] The saturated magnetization and remanence of these ribbons or powders are relative low. Yang et al. optimized melt spinning and annealing processes of the MnBi ribbons.[190] They found that the grain size of 200 nm in the 20 m/s spun ribbons can be reduced to 20–30 nm with increasing wheel speed to 65 m/s. With a grinding process followed by alignment under magnetic field, an anisotropic nanocrystalline MnBi magnet is obtained with an energy product of 7.1 MGOe. The hysteresis loops of the anisotropic MnBi magnets are given in Fig.
 | Fig. 21. (color online) The magnetic properties of nanocrystalline MnBi. (a) The hysteresis loops of MnBi at room temperature along the directions parallel and perpendicular to the c-axis; (a) the temperature dependence of coercivity.[190] |
Recently, the Co-rich transition-metal alloys such as HfCo7 and Zr2Co11 have attracted interests to develop new RE-free magnetic materials with high-energy products. The metastable nature and/or the requirement of high formation temperature of about 1050–1230 °C for HfCo7 phase indicate that melt spinning process is suitable to make such alloy with good phase purity. Although Zr2Co11 phase has a wider temperature range of about 300–1254 °C, a high-temperature growth or annealing process followed by melt spinning was generally used to obtain high-anisotropy crystal structures in the alloys. Balasubramanian et al. fabricated the nanocrystalline Co100−xTMx alloys (TM = Zr, Hf, and 
Several RE-free magnets have L10-type structure, such as Fe–Pt and Mn–Al. Zhang et al. studied the phase evolution, thermal stability and magnetic properties of the melt-spun Fe70−xPtxB30 ribbons.[196] It was found that the amorphous forming ability increases with small amount addition of Pt into the Fe70B30 alloy and a complete amorphous phase is obtained in the alloys with x = 5 and 10 and wheel speed of 33 m/s. However, further increase of Pt content results in the formation of fcc-FePt, Fe2B with or without L10-FePt phases. A homogenous microstructure, consisting of magnetically hard L10-FePt and soft Fe2B phases with an average grain size of 30–50 nm, is formed in the ribbons with x = 10–20 after appropriate annealing. The coercivity of Fe70−xPtxB30 ribbons increases while remanence decreases with increasing Pt content. Good magnetic properties were obtained in the Fe70−xPtxB30 ribbons with μ0Mr = 0.81–1.20 T, μ0Hc = 0.22–0.65 T, and (BH)max = 8.0–11.0 MGOe.
Liu et al. studied the effects of C, B, and RE doping in phase transitions and magnetic properties of Mn–Al alloy.[197] The as-spun Mn–Al, Mn–Al–C, and Mn–Al–C–RE ribbons possessed a hexagonal ε phase. The ε to L10 phase transition occurs at ∼500 °C, which is of interest as it could develop hard magnetic properties in the ribbons. Moderate carbon addition promotes the formation of the desired magnetically hard L10 phase and improves the hard magnetic properties. The best magnetic properties, μ0Mr = 0.3 T, μ0Hc = 0.15 T, and (BH)max = 1.5 MGOe, were obtained in Mn–Al–C ribbon with C content of 1.7 at.% annealed at 650 °C, though they are quite low compared to other permanent magnets.
Löwe et al. studied the magnetic properties of melt-spun Alnico ribbons.[198] The grain size of the ribbons decreases from 


Advanced permanent magnet applications always require materials with high remanence, high coercivity, and high Curie temperature. Although most single-phase permanent magnets have large coercivity, their saturation magnetization is relatively low compared to that of magnetically soft materials such as Fe or Fe–Co. In addition, the rare-earth magnets are chemically reactive and expensive on account of a substantial content of rare-earth elements. It is natural to think that the combination of magnetically hard and soft materials should give higher magnetization and thus a potentially higher energy product with lower material cost. Coehoorn et al.[199–201] and Shen et al.[32,202–204] first reported the pioneering researches on the Nd2Fe14B/Fe3B composites with Fe3B as the magnetically soft phase and with the microstructure in nanoscale. The nanocomposites with the magnetically hard and soft phases have attracted tremendous attention in searching for novel permanent magnets, especially after the concept of exchange-spring magnets was first introduced by Kneller and Hawig in 1991.[13] In such exchange-spring magnets, the magnetically hard phase provides a high coercivity and the magnetically soft phase provides high magnetization. If the two phases are magnetically coupled together in an efficient way, the resultant composites can have both high coercivity and high magnetization, which eventually give a higher maximum energy product than the single-phase hard magnets. The concept was further developed by Skomski and Coey[14] who showed that the length scale of the soft phase should be smaller than twice of the domain wall width (δB) of the magnetically hard phase. For example, δB of Nd2Fe14B is about 4.2 nm which leads to a critical size smaller than 10 nm for the magnetically soft phase. The magnetically soft phase becomes a slave to the magnetically hard phase and follows its magnetization direction, as illustrated in Fig.
 | Fig. 22. (color online) Schematic of the exchange-spring principle from Ref. [205]. A magnetically hard phase possessing a wide hysteresis loop exchange couples to a magnetically soft phase possessing a tall hysteresis loop, forming a composite magnet that has both a wide and tall hysteresis loop. The image to the right illustrates a bilayer structure. If the soft layer thickness exceeds a critical size, the magnetization reversal happens first in the soft layer. |
The magnetic properties of the exchange-coupled nanocomposite magnets depend sensitively on both the material parameters, such as the magnetocrystalline anisotropy and saturated magnetization, and the microstructure, such as the grain size, soft-phase content and soft phase distribution. In principal, the nanocomposite could be made of any magnetically hard phase discussed in Section
Coehoorn et al. first obtained this novel nanocomposite magnet consisting mainly of Fe3B with Nd2Fe14B as a secondary phase.[199] The amorphous alloy with composition of Nd4Fe78B18 was produced by melt spinning, followed by post annealing at 670 °C for 30 minutes. The annealing process consists of two steps: the metastable phase Fe3B is crystallized with a small amount of α-Fe phase at a lower temperature at first, while the hard-magnetic phase Nd2Fe14B is formed at a higher temperature. The annealed ribbons consist of 73% Fe3B, 12% α-Fe, and only 15% magnetically hard phase Nd2Fe14B. The saturated magnetization of Fe3B and Nd2Fe14B are both 1.6 T at room temperature, while Fe3B has a higher Curie temperature of about 513 °C, nearly 200 °C higher than that of Nd2Fe14B. The annealed ribbon gives a coercivity of 0.3 T, which may be due to the presence of Nd2Fe14B since Fe3B has much lower magnetocrystalline anisotropy. The most remarkable property in this material is the normalized remanence, which is as high as 0.75 and much higher than 0.5 predicted by Stoner–Wohlfarth model. The large remanence enhancement is attributed to the fine microstructure with Fe3B grains of 30 nm and Nd2Fe14B grains of 10 nm plus the exchange coupling between them. Owing to the large remanence, the energy product of 11.9 MGOe is obtained.[200] With partial substitution of Nd by Tb or Dy, the coercivity of the melt-spun ribbons can be improved to 0.45 T.[201] Simultaneously, Shen et al. studied the amorphization and crystallization of the rapidly quenched M1−x(Nd2Fe14B)x ribbons (M = Fe3B, Fe2B; 
Kim et al. studied the ferromagnetic phase diagram of the NdxFeyBz (








 | Fig. 23. (a) Ferromagnetic phase diagram and (b) coercivity contour of the optimally annealed NdxFeyBz (


|
The substitutions for either rare earth or transitional metal elements could affect the magnetic properties of melt-spun ribbons. Cheng et al. reported that the substitution of R (R=Y, Pr, Gd, or Dy) for Nd in RxNd4−xFe77.5B18.5 alloys results in the decrease of coercivity with Y, Pr, Gd substitution.[172,207] A small amount of Dy addition improves the coercivity but full substitution of Dy also decrease coercivity due to the presence of magnetically soft phase Dy3Fe62B14. It was interesting that the melt-spun Nd–Fe–B alloys annealed at 670 °C for 2 minutes consist of only body-centered-tetragonal (bct) Fe3B and a few percent of α-Fe but no Nd2Fe14B phase. In addition, about 5 at.% Fe atoms in the Fe3B phase are replaced by Nd in the annealed ribbons, which enhanced the hard-magnetic properties of Fe3B. It was further found that the substitutions of Pr, Gd, and Dy do not influence the hyperfine field for 57Fe in α-Fe, but increase the hyperfine field for 11B in bct-Fe3B. This leads to a conclusion that the hard-magnetic properties of melt-spun Nd–Fe–B result from bct-Fe3B containing Nd atoms, but not from the presence of the magnetically hard Nd2Fel4B phase.[207] Kanekiyo et al. further improved the magnetic properties of the Fe3B/Nd2Fe14B nanocomposite by Dy addition with remanence of 1.15 T, coercivity of 0.5 T and energy product of 16.5 MGOe.[208]
Xiao et al. studied the effects of grain size and anisotropy of magnetically hard phase on the magnetic properties of B-rich Nd4−xSmxFe77.5B18.5 (x = 0–0.5) alloys through annealing control and Sm substitution for Nd.[209] It was found that the grain sizes of the soft phase Fe3B is about 16 nm and 23 nm for 670 °C and 760 °C annealed ribbons, respectively. These grain sizes are larger than the critical size of about 10 nm for magnetically soft phase, predicted by the Kneller–Hawig model.[13] However, effective exchange coupling was observed in the Sm-substituted ribbons, which indicates that the Sm substitution reduced the anisotropy constant of magnetically hard phase and thus caused the extension of critical length for magnetically soft phase.[209]
Shen et al. studied the Co substitution for Fe in the Nd4(Fe1−xCox)77.5B18.5 alloys and found that the Curie temperatures of both the as-quenched amorphous and annealed ribbons increase with Co content.[204] Interestingly, it was observed that the magnetic moment of Fe atom increases with increasing Co content from x = 0 to x = 0.4, while the magnetic moment of Co atom keeps a constant value over the whole concentration range. Unfortunately, the coercivity decreases monotonically with increase of Co concentration. A still good magnetic property was observed in the ribbons with 

Kanekiyo et al. have reported that Al, Si, Cu, Ga, Ag, Au additives considerably reduce grain size of (Fe,Co)3B/Nd2Fe14B nanocomposite based on Nd5Fe71.5Co5B18.5M alloy, where M is the above-mentioned elements.[211] For example, the optimally heat-treated ribbons of Nd5Fe76.5B18.5 have grains around 40–50 nm, while the Ga or Al combined with Co addition could reduce the grain size down to 10–20 nm in the Nd5Fe71.5Co5B18.5M ribbon. The grain refinement increases the remanence from 1.0 T for Nd5Fe76.5B18.5 ribbon to 1.08–1.20 T for the Nd5Fe71.5Co5B18.5M ribbons, where Si additive gives the highest value. The Cu additive provides the lowest remanence among the M-added samples, but it generates the largest coercivity around 0.45 T. On the other hand, Ga-added ribbons have the largest energy product of about 16 MGOe. Ping et al. found that Cu and Nb can refine the microstructure of the Fe3B/Nd2Fe14B using TEM and atom probe field ion microscopy (APFIM).[212] Figure 

 | Fig. 24. TEM bright field micrographs of (a) Nd4.5Fe77B18.5, (b) Nd4.5Fe76.8B18.5Cu0.2, (c) Nd4.5Fe
|
Cheng et al. reported that the carbon substitution for B reduces the crystallization temperature of the as-spun Nd4Fe77.5B18.5 amorphous alloy.[214] Unfortunately, the coercivity of the crystallized ribbons decreases with increasing carbon content, with a simultaneous development of an orthorhombic Fe3B (o-Fe3B) phase, instead of the bct-Fe3B phase.
Although researches still occasionally occur recently, it is concluded that the energy product of Fe3B/Nd2Fe14B nanocomposite magnets is relatively low due to the relatively low saturated magnetization of Fe3B phase. Their coercivity is relative low comparing to other nanocomposites, so it is not critical to understand where is the coercivity from, either the bct-Fe3B phase or Nd2Fe14B phase. The magnetic properties of some typical Fe3B/Nd2Fe14B nanocomposite magnets prepared by melt spinning are summarized in Table
| Table 8. μ0Mr, μ0Hc, and (BH)max of Fe3B/Nd2Fe14B nanocomposite magnets with different compositions. . |
The α-Fe phase is actually often observed in the Fe3B/Nd2Fe14B nanocomposite as mentioned in Section
The microstructure control, such as grain size, is one of the key factors to achieve high remanence and coercivity in the nanocrystalline and nanocomposite magnets. Davies et al. studied the effects of grain size on the remanence and coercivity of the single-phase nanocrystalline Nd13.2Fe79.6B6Si1.2 magnets.[215] It is observed that remanence enhancement begins when grain size falls below ∼30 nm for both surfaces of the melt-spun ribbons, i.e., roller and free surfaces. The phenomenon is believed to result from exchange coupling between grains when they are free of non-magnetic intergranular phase. This condition correspondingly leads to reduction of coercivity since it lowers the resistance to reverse magnetization, as shown in Fig. 
 | Fig. 25. (color online) (a) Dependence of remanence and coercivity on grain size of melt-spun Nd13.2Fe79.6B6Si1.2 ribbons. (b) Dependence of magnetic properties on Nd content of melt-spun Nd8+xFe86−xB6 ribbons. The figures are reproduced from Ref. [215]. |
Besides the grain size control, the soft-phase component is another key factor to achieve good magnetic properties in nanocomposite Nd2Fe14B/α-Fe magnets. Bauer et al. studied the effect of α-Fe phase content (up to 40 vol.%) on magnetic properties of the composite magnets, starting from nearly single-phase Nd2Fe14B magnets.[73] The maximum remanence μ0Mr = 1.25 T with μ0Mc = 0.53 T and (BH)max = 23.2 MGOe were achieved in nanocomposite magnets containing 30 vol.% α-Fe (as shown in Fig.
 | Fig. 26. (color online) Dependence of magnetic properties of NdFeB-based nanocomposite magnets on α-Fe content at room temperature. The figure is reproduced from Ref. [73]. |
 | Fig. 27. (a) TEM micrograph and (b) grain size distribution of melt-spun Nd10Fe84B6 ribbon with 14.2 vol.% α-Fe.[73] |
The element substitutions in the Nd2Fe14B/α-Fe affect the microstructure and thus magnetic properties, which are categorized into RE substitution, refractory element substitution and other element substitution, as summarized below. The magnetic properties of the element substituted melt-spun ribbons are also summarized in Table
| Table 9. μ0Mr, μ0Hc, and (BH)max of Nd2Fe14B/α-Fe nanocomposite magnets with different compositions and different element substitutions. . |
 | Fig. 28. TEM images for the (a) Nd12Fe82B6 and (b) Nd10Nb2Fe82B6 ribbons spun at 15 m/s.[223] |
It is interesting to note that the magnetic field during melt spinning process may also reduce the grain size in the ribbons. Nguyen et al. customized a melt spinner which could provide a magnetic field up to 0.32 T parallel or perpendicular to the ribbons plane during the melt-spinning process.[230,231] The grain refinement effect was proved by TEM observations in the single-phase Nd15Fe77B8 ribbons, as shown in Fig.
 | Fig. 29. TEM images of Nd15Fe77B8 ribbons melt-spun at the wheel speed 25 m/s (a) without a field and (b) in the field of 0.15 T which is perpendicular to ribbon plane.[230] |
The intrinsic magnetic properties of Pr2Fe14B are similar to those of Nd2Fe14B, but Pr2Fe14B does not have spin reorientation behavior, so it can be used at low temperature. In addition, Pr2Fe14B has slightly higher anisotropy field than Nd2Fe14B, as shown in Table
| Table 10. μ0Mr, μ0Hc, and (BH)max of Pr2Fe14B/α-Fe nanocomposite magnets with different compositions and different element substitutions. . |
Goll et al. studied the effects of composition on microstructure and magnetic properties of Pr2Fe14B/α-Fe two-phase magnets from the stoichiometric Pr2Fe14B to a nominal composition with 54.2 vol% α-Fe.[74] The room temperature magnetic properties of the Pr2Fe14B/α-Fe ribbons are summarized as a function of the α-Fe concentration, as shown in Fig. 


 | Fig. 30. (color online) Magnetic properties as a function of the α-Fe phase content of nanocomposite Pr2Fe14B/α-Fe magnets.[74] |
 | Fig. 31. (a) TEM image of a melt-spun Pr8Fe87B5 ribbon containing 30.4 vol% α-Fe; (b) grain size distribution of a melt-spun Pr10Fe84B6 ribbon containing 14.0 vol% α-Fe.[74] |
The effects of the grain size on magnetic properties of a series of nanocrystalline melt-spun PrxFe94−xB6 alloys (6
It is interesting to note that high pressure leads to grain refinement and thus more efficient exchange coupling in the Pr2Fe14B/α-Fe nanocomposites. Wang et al. reported this high pressure effects in the Pr8Dy1Fe74.5Co10Nb0.5B6 ribbons.[233] The grain size of Pr2Fe14B phase decreases from 22.5 to 8.7 nm, while the grain size of α-(FeCo) phase also drops from 30.3 to 10.1 nm, when increasing pressure from 125 MPa to 5 GPa. As a result, the magnetic properties are improved from 1.03 T, 0.87 T, and 17.1 MGOe to 1.11, 1.02 T, and 23.6 MGOe for remanence, coercivity, and energy product, respectively. However, when hot pressing under even higher pressure, the crystallization is constrained and the hot-pressed magnets retains a certain amount of amorphous phase besides the Pr2Fe14B and α-(FeCo) phases, which results in the deterioration of the magnetic properties.
Similar to Nd2Fe14B/α-Fe, element substitutions, such as RE, refractory elements, and other elements, can help on grain refinement and grain boundary modifications of the Pr2Fe14B/α-Fe magnets, leading to improved magnetic properties. Chen et al. found that Dy substitution for Pr not only increases the coercivity because of the much higher magnetocrystalline anisotropy of Dy2Fe14B alloys, but also leads to the microstructure refinement in the Pr2Fe14B/α-Fe nanocomposite magnets.[234] An optimum coercivity of 0.66 T is obtained in the Pr7Dy1Fe86B6 magnet as compared to 0.43 T in the Pr8Fe86B6 magnet. As a result, the energy product increases from 9.1 MGOe in the Dy-free magnet to 16.9 MGOe in the 1 at.% Dy magnets, due to the enhanced exchange coupling between the magnetically hard and soft phases. As mentioned in Section
Zhang et al. investigated the Co substitution for Fe in the melt-spun Pr9Fe86−xCoxB5 (x = 0–16) nanocomposites.[235] It was found that Co obviously raises the saturated magnetization from 1.50 T for Pr9Fe86B5 to 1.80 T for Pr9Fe76Co10B5 (measured under an applied field of 6.5 T), which may be attributed to the formation of α-(Fe, Co) phase. At the same time, the remanence, coercivity, and maximum energy product changes from 0.96 T, 0.57 T, and 11.8 MGOe to 1.15 T, 0.63 T, and 17.3 MGOe, respectively. Further substitution of Co for Fe results in a decrease of magnetic properties because of the presence of minor amounts of 1:5 and 2:17 phases. It was also observed that the Curie temperature of the magnetically hard phase increases linearly by increasing Co-substitution at the rate of ΔTc = 9 °C/at%.
Chang et al. found that both Pr2Fe23B3 and Fe3B phases have been completely suppressed and the volume fraction of magnetically hard phase Pr2Fe14B increases in the Pr9.5Fe78.5M2B10 (M = Cr, Nb, Ti, V, and Zr) ribbons with all the selected refractory element substitutions.[236] Accordingly, the coercivity of the ribbons is improved remarkably from 0.83 T for ternary Pr9.5Fe80.5B10 ribbons to 1.01–1.32 T for all chosen refractory element-substituted nanocomposites. The optimal magnetic properties with an energy product of 16.9 MGOe is obtained in Nb-substitution Pr9.5Fe78.5Nb2B10 ribbons. Chen et al. confirmed that the largest property enhancement is obtained in Nb-substituted Pr8Fe84Nb2B6 magnets with a coercivity of 0.65 T and a maximum energy product of 17.9 MGOe, as compared to the coercivity of 0.43 T and the energy product of 9.1 MGOe in the Pr8Fe86B6 magnets.[97] The gain of the magnetic properties is attributed to the most uniform microstructure with the smallest average grain size of 10–20 nm in the Nb-substituted magnets. Ti substitution has a very similar role as Nb substitution in the Pr2Fe14B/α-Fe but with a slightly poorer performance, which is also similar to their function in the Nd2Fe14B/α-Fe nanocomposite magnets.
Yang et al. reported significant improvements of microstructure and magnetic properties of Pr2Fe14B/α-Fe nanocomposite magnets by Cu and Mn substitutions for Fe.[237] It was found that Mn is more effective on the enhancement of coercivity than Cu. The remanence has maximum values when the content of Cu and Mn reaches 0.2 and 0.6, respectively. The remanence of the ribbons with Mn substitution again has higher value than that with Cu substitution, which may be attributed to magnetic dilute effect of nonmagnetic element Cu. The saturated magnetization decreases from 1.68 T for Pr8Fe87B5 to 1.61 T for Pr8Fe86.4B5Cu0.6 ribbons, while that of Pr8Fe86.4B5Mn0.6 only deceases to 1.65 T. In comparison with Cu substitution, the Mn substitution significantly improves the (BH)max, which mainly results from the stronger exchange-coupling effect due to fineness of grain in the melt-spun Pr8Fe87−xB5Mnx ribbons. Excellent magnetic properties with remanence of 1.33 T, coercivity of 0.58 T, and energy product of 23.1 MGOe are obtained in the Pr8Fe86.4B5Mn0.6 ribbons. The authors also studied the effects of addition of V or C or the combined addition on the structure and magnetic properties of melt-spun Pr8Fe86−xVxB6−yCy ribbons.[238] Compared with addition-free ribbons, 1 at.% V addition is found to reduce the grain sizes and improve their magnetic properties due to a strong exchange coupling between the magnetically hard and soft phases. A normalized remanence of 0.82, a coercivity of 0.62 T, and a maximum energy product of 23.4 MGOe in melt-spun Pr8Fe85VB6 ribbons are obtained at room temperature. The combined addition of V and C leads to the formation of an intermediate phase of VC at grain boundaries, which appears as a pinning barrier during magnetization and results in a slight increase of the coercivity value to 0.69 T for melt-spun Pr8Fe85VB5C ribbons. However, energy product drops to 21.7 MGOe for the ribbons with C substation. Zhang et al. studied the effect of Ga additive on the microstructure and magnetic properties of nanocomposite Pr2(Fe, Co)14B/α–(Fe, Co) ribbons.[239] The microstructure refinement by introducing 1 at.% Ga leads to a stronger exchange coupling between the magnetically hard and soft phases in comparison with that in Ga-free sample. Therefore, the remanence and energy product increase from 1.14 T, 17 MGOe for Ga-free ribbons to 1.22 T, 22.2 MGOe for the Ga-added ribbons.
The compound Sm2Fe15Ga2C has an anisotropy field exceeding 12 T at room temperature, which is much larger than those of Nd2Fe14B and Pr2Fe14B (7.6 and 9.0 T, respectively). However, the introduction of nonmagnetic Ga atoms decreases the saturated magnetization monotonically. As a result, the saturated magnetization is only about 1.0 T, which is much lower than those of Nd2Fe14B and Pr2Fe14B. In order to obtain high-energy product, it is necessary to improve the saturated magnetization and remanence, while keeping the coercivity sufficiently high. Exchange coupled nanocomposite magnets meet this requirement as magnetically hard phase Sm2Fe15Ga2C can provide large coercivity while magnetically soft phase α-Fe can provide high magnetization.
Since Sm is easy to evaporate during alloying, it may be difficult to control the grain size and its distribution precisely by directly melt spinning, especially for the Sm2Fe15Ga2C-based nanocomposite with low Sm concentration. Cheng et al. first fabricated the Sm2Fe15Ga2C/α-Fe nanocomposites with low Sm contents directly by melt spinning without a subsequent heat treatment in 1998.[241] The alloy with nominal composition Sm8Fe72Ga8C12 was melt-spun at a wheel speed of 15–35 m/s. It was found that the wheel speed affects the microstructure sensitively. The ribbons quenched at 15 and 17.5 m/s are composed of a phase with the Th2Zn17-type structure and α-Fe, while those quenched at 25 m/s and above show nearly complete amorphous state. The average grain size of Sm2Fe15Ga2C and α-Fe are found to decrease with increasing the wheel speed from 140 and 50–60 nm for 15 m/s to 60–70 and 20–30 nm for 18.5 m/s, respectively. A maximum energy product of 5.9 MGOe was obtained for ribbons spun at 17.5 m/s with remanence of 0.71 T and coercivity of 0.55 T. The authors further found that Zr additive in the above nanocomposites could lead to the microstructure refinement and significantly improve the magnetic properties.[242] Figure
 | Fig. 32. (a) TEM images and (b) grain size distributions for the Zr-free (Sm8Fe72Ga8C12) and Zr-containing (Sm7.9Fe71.3Ga7.9Zr1C11.9) ribbons.[242] |
 | Fig. 33. Room-temperature hysteresis loops of the Zr-free (Sm8Fe72Ga8C12) and Zr-containing (Sm7.9Fe71.3Ga7.9Zr1C11.9) ribbons.[242] |
Zhang et al. studied the magnetic properties of Sm2Fe15Si2C/α-Fe nanocomposites with Cu additive, which are prepared by melt spinning at wheel speed of 20 m/s.[243] The average grain size of 2:17 carbides and α-Fe in the ribbons is about 50 and 30 nm, respectively. The ribbons exhibit a single hard magnetic phase behavior and remanence enhancement due to inter-grain exchange coupling between magnetically hard and soft phases. The remanence increases with the increase of α-Fe phase content in ribbons, while the coercivity decreases rapidly, which agrees with the correlation between remanence and coercivity in other nanocomposite magnets. The highest maximum energy product around 10.7 MGOe was obtained for Sm8Fe76Cu4Si8C4 ribbons with a coercivity of 0.5 T.
The effect of pressure on the microstructure of Sm2(Fe,Si)17Cx/α-Fe nanocomposite magnets has been studied by Zhang et al. through pressing the amorphous Sm8Fe85Si2C5 alloy under pressures up to 6 GPa at 650 °C.[244] The grain size of α-Fe and Sm2(Fe,Si)17Cx decreases from 30.6 to 6.4 and from 28.5 to 5.8 nm, respectively. The volume fraction of the 2:17-type carbide increases with increasing pressure. A significant increase in both remanence and coercivity, comparing to those prepared under normal pressure, is observed in the nanocomposites prepared under high pressure. As a result, an energy product is significantly improved in the Sm2(Fe,Si)17Cx/α-Fe nanocomposites.
| Table 11. μ0Mr, μ0Hc, and (BH)max of Sm2Fe15M2C/α-Fe (M = Ga, Si) nanocomposite magnets with different compositions and different element substitutions . |
The 2:17-type Sm(CoFeCuZr)z magnets, having the highest Curie temperature among the commercial rare-earth permanent magnets, have attracted considerable interest for high-temperature applications since 1970 s, because of their large energy products and high temperature performance.[245] Their high coercivity is widely believed to be domain-wall-pinning control, which is attributed to the cellular microstructure having a 2:17 matrix and 1:5 precipitates around the grain boundaries of the 2:17 phase. Therefore, these 2:17-type magnets are also called as precipitation-hardened magnets. In addition to the cellular microstructure, a platelet phase of few nanometers in width which is orientated perpendicular to the c axis is superimposed on the cellular microstructure. This so-called lamellar Z phase extends through quite a lot of cells and cell boundaries and is believed to be of the hexagonal 2:17 structure or of the rhombohedral 1:3 structure. The special microstructure in the conventional sintered magnets is usually obtained through a complex heat treatment, as schematized in Fig.
Doll et al. fabricated the precipitation-hardened ribbons through the melt spinning process and appropriate post heat treatment for the first time.[249] Although the alloys are prepared by melt spinning, however, the annealing procedure is very similar to that of conventional sintered magnets, i.e., Th = 1160 °C, th = 30 min, Ta = 840 °C, ta = 19 h, and cooling rate of 0.75 °C/min. TEM analysis shows that a rhombic structure parallel to the c axis and a hexagonal network in the basal plane are formed in the ribbons after annealing, which is very similar to the microstructure of the sintered magnets. The characteristic cell size is about 50–70 nm, which depends on the composition. Figure
 | Fig. 35. (color online) (a) Temperature dependence of the coercivity of Cu/Fe-rich and Cu/Fe-poor in comparison with other common permanent magnetic materials; (b) EDX profiles of Sm, Cu, Fe, and Zr (contents standardized to the Co content) in the vicinity of a 2:17/1:5 phase boundary in Cu/Fe-poor magnet.[249] |
Yan et al. further simplified the process for the melt-spun Sm(CoFeCuZr)z ribbons and found that the homogenizing process (solid solution treatment) actually is not necessary.[250] They compared the magnetic hardening processes of the Sm(Co0.74Fe0.1Cu0.12Zr0.04)7.5 ribbons with and without solid solution treatment (homogenizing at 1160 °C for 4 hours). The coercivity of the ribbons with solid solution treatment continues to increase with longer isothermal aging time and a value of 2.4 T is obtained after aging for 12 h at 850 °C, as shown in Fig.
 | Fig. 36. (a) Evolution of the coercivity dependent on the isothermal aging time at 850 °C for the Sm(Co0.74Fe0.1u0.12Zr0.04)7.5 ribbons with and without solid solution treatment; (b) typical TEM micrographs of samples without solution treatment.[250] |
It is very interesting that Yan et al. observed the disappearance of the large coercivity in the above melt-spun Sm(CoFeCuZr)z magnet by an additional short time aging.[251] Figure
 | Fig. 37. (a) Dependence of the coercivity of Sm(Co0.74Fe0.1Cu0.12Zr0.04)7.5 ribbons on aging temperature (additional isothermal aging for 5 min); (b) nanoprobe EDX profiles of Cu across the interface between the 2:17 matrix and the 1:5 grain boundary of the ribbons before (sample A) and after (sample B) additional aging at 850 °C for 5 min.[251] |
Rong et al. found that the TbCu7-type 1:7 phase is formed by direct melt spinning in the Gd(Co0.88−xCuxFe0.09Zr0.037 alloy as well.[252] It is confirmed that solid solution treatment and the isothermal aging are not necessary for precipitation hardening in the melt-spun materials, i.e., high coercivity can be obtained by simply slow cooling the ribbons from 850 to 400 °C. Figure 
 | Fig. 38. TEM micrographs of the Gd(Co0.88−xCuxFe0.09Zr0.03)7 ribbons. (a) As-spun; (b) precipitation-hardened without isothermal aging; (c) and (d) one 1:7 region of (b) which is observed perpendicular and parallel to the c axis, respectively.[252] |
 | Fig. 39. (color online) Temperature dependences of remanence and coercivity of the precipitation-hardened Gd(Co0.88−xCuxFe0.09Zr0.03)7 ribbons without isothermal aging.[252] |
Besides the simplified precipitation hardening process, texture can be developed in melt-spun Sm(CoFeCuZr)z ribbons, without the conventional sintering process. Therefore, a relatively high energy product can be obtained in such ribbons. Rong et al.[253,254] and Yan et al.[139] have studied the effects of composition on the crystallographic texture of the precipitation-hardened 

 | Fig. 40. XRD patterns of melt-spun and precipitation-hardened Sm(Co0.87−xCuxFe0.1Zr0.03)7 ribbons with different Cu contents.[253] |
 | Fig. 41. XRD patterns of the melt-spun ribbons (a) Sm(Co0.87−yFeyCu0.1Zr0.03)7 with different Fe contents; (b) Sm(Co0.8−wFe0.1Cu0.1Zrw)7 with different Zr contents.[253,254] |




 | Fig. 42. (color online) SEM images of the free surface of melt-spun Sm(Co0.8−wFe0.1Cu0.1Zrw)7 ribbons: (a) w = 0.01, (b) w = 0.04, and (c) w = 0.08.[254] |
The desired magnetic properties of Sm(CoFeCuZr)z ribbons are controlled not only by the composition and texture, but also by the heat-treatment process, i.e., the isothermal temperature and time, the cooling rate, and the final quench temperature. The systematically work to optimize the magnetic properties of Sm(CoFeCuZr)z melt-spun ribbons was reported in Refs. [253] and [255].
Figure 


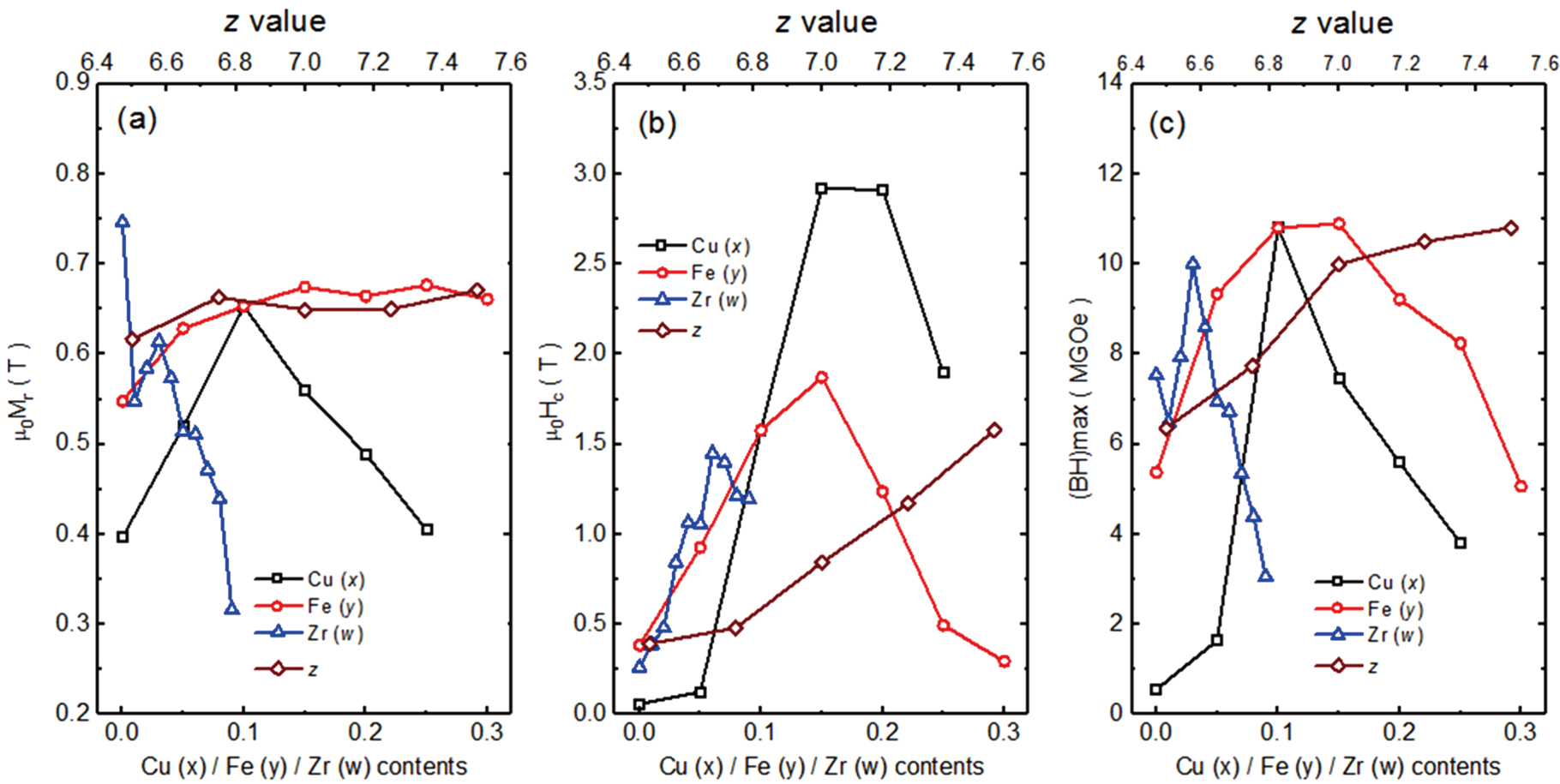 | Fig. 43. (color online) The compositional dependence of (a) μ0Mr, (b) μ0Hc, and (c) (BH)max of precipitation-hardened 
|
Besides the composition, the control of precipitation hardening process is another critical factor for the coercivity development in Sm(CoFeCuZr)z ribbons. Figure
Coercivity is low when Ta is lower than 750 °C, while it increases quickly with varying Ta up to 900 °C. Further increase of Ta to 950 °C and above leads to a drop of coercivity.
The optimized ta depends on the composition. For example, the coercivity of the ribbons with Cu content x = 0.15 increases monotonically until ta = 3–5 h and then rarely changes with longer aging time. However, the coercivity of the ribbons with x = 0.25 reaches a maximum at ta = 1 h (not shown in the figure), i.e., a short-time aging is enough to develop the coercivity and a long-time aging deteriorates the ribbons.
The coercivity increases monotonically with reducing the cooling rate vc, although degree of influence may rely on the composition, such as Cu content. This is understandable as Cu diffusion happens at this stage. For the ribbons with larger Cu content, the Cu concertation in the 1:5 boundary phase may be saturated faster, so an extremely low vc may not help to increase the coercivity. However, for the ribbons with lower Cu content, a very low vc could lead more Cu diffused into the 1:5 boundary phase and thus significant increase of coercivity.
 | Fig. 44. (color online) The effects of isothermal aging temperature (Ta), aging time (ta), cooling rate (vc), and quench temperature (Tq) on the room-temperature coercivity of Sm(Co0.72Fe0.1Cu0.15Zr0.03)7 ribbon.[255] |
The coercivity increases fast with a decrease in the quenching temperature Tq. Similar to the effects of vc during the slow cooling, the decrease in Tq leads to an increase of Cu concentration in the 1:5 boundary phase and thus an increase in coercivity.
As mentioned above, the composition affects temperature dependence of coercivity Hc(T). In fact, all parameters of the precipitation hardening process affect the temperature dependence of coercivity as well. Figure 
 | Fig. 45. (color online) Hc(T) curves of the Sm(Co0.77Fe0.1Cu0.1Zr0.03)7 ribbons with different quenching temperatures.[255] |
Exchange coupling is the way in which two magnetic atoms in a material interact with each other. When two magnetic atoms are situated very close together, their electrons can interact directly, in the same way as when forming a chemical bond. This type of exchange coupling is the way happened in the magnetic materials. The generalized intergrain exchange coupling (IGEC) actually includes inter-phase exchange coupling which happens between two phases in the nanocomposite magnets, and the inter-grain exchange coupling between the grains with the same phase which could happen in either single-phase nanocrystalline magnets or nanocomposite magnets. The IGEC plays the key role in determining the magnetic properties for nanostructured magnetic materials, especially for nanocomposite magnets. It should be noted that the discussions in this section are not limited to the melt-spun materials but they may be extended to any nanocrystalline magnets fabricated by other techniques, such as ball milling, thin-film technologies, self-assembly.
If a two-phase nanocomposite magnet has microstructure with fine grains and homogenous distributed magnetically soft-phase together with strong IGEC, it should demonstrate a one-step reversal behavior in the demagnetization curve, i.e., there is no “kink” in the curve, which is the so-called single-phase magnetic behavior. However, if the IGEC is not efficient or the microstructure is not well controlled, the demagnetization curve often shows a two-step reversal behavior, i.e., there is a “kink” in the curve. This method is widely used to inspect the effects of IGEC in the nanocomposite magnets in a simple way. Figure
 | Fig. 46. (color online) (a) Demagnetization curves of the composite samples milled for different time; energy-filtered transmission electron microscopy (EFTEM) images of Fe maps for the samples milled for (b) 30 min, (c) 1 h, and (d) 4 h. High Fe-content regions have bright contrast.[256,257] |
It should be noted that exchange-coupled magnets exhibit a strong temperature dependence of their hysteresis loops. Some nanocomposite magnets may have a smooth hysteresis loops at room temperature, but their low-temperature loops show a two-phase demagnetizing behavior. This could be explained by the reduction of exchange length 
 | Fig. 47. Demagnetization curves at different temperatures of Pr8Fe87B5 nanocomposite magnets prepared by melt spinning.[258] |
While the method of single-phase magnetic behavior can provide an intuitive information, it only provides qualitative information of the strength of exchange coupling in the magnets. In addition, this method cannot provide good information for single-phase nanocrystalline magnets as there is no kink even there is no exchange coupling.
According to the Stoner–Wohlfarth (SW) model, for an assembly of non-interacting and randomly oriented grains, the ratio of the remanence to the saturation magnetization (normalized remanence) is
 |
To quantitatively analyze the effect of IGEC on the normalized remanence, Zhang et al. estimated the maximum mr, assuming that the mean magnetization direction of each hard grain boundary region is in the middle orientation between easy magnetization axis of the grain and that of its neighboring hard grain, while the magnetization direction of soft grain (such as α-Fe) is assumed to be in the same mid-way.[258] The sum of all such regions for the remanence is
 |
 |
Zhao et al. studied the remanence enhancement in a grain chain through a more complicated analytical model.[259] In this model, the magnetic moments near the grain boundaries point to the directions which gradually change from the easy direction of one grain to that of a neighboring grain, instead of the simple average of two directions of the easy axes, while those in the grain center point to the direction of the easy axis. The two-dimensional analytical model generates a normalized remanence given by
 |


 |
Rong et al. studied the contribution of IGEC on the remanence of the isotropic nanocrystalline magnets using micromagnetic finite element analysis (FEA).[15] Figure
 | Fig. 48. (color online) Dependence of mr as a function of grain size in the single-phase nanocrystalline magnet. FEA results are from Ref. [15]; analytical results are based on Eq. ( |
The analysis of remanence enhancement in the nanocomposites is much more challenge than that in the single-phase nanocrystalline magnets, as the magnetically soft grains are more easily affected by the dipolar interactions comparing to the magnetically hard grains. This complex makes the accurate analysis of remanence enhancement by analytical model almost impossible. On the other hand, micromagnetic FEA simulation could provide a much better estimation on the remanence enhancement.[15–17,260] Figure
 | Fig. 49. (color online) Calculated mr of the isotropic nanocomposite as a function of soft phase content, vs, with and without considering the dipolar interactions.[15] |
Measurements of remanence are a well-known tool to characterize IGEC in the nanocrystalline magnets by comparison with an ideal Stoner–Wohlfarth (S–W) assembly. The remanence enhancement mentioned in Section 4.2 is only one of the methods which only considers the saturated remanence, i.e., remanence measured after saturating the magnet first. Henkel plot is another useful and popular way to investigate the IGEC inside magnetic materials. In this method, two types of remanence must be measured. One is the magnetizing remanence Mr(H) which is acquired after the application and subsequent removal of a direct applied field H. It should be noted that Mr(H) must be measured from the specially prepared initial zero-magnetization state, such as thermally demagnetized. The other is demagnetizing remanence Md(H) which is obtained after saturation in one direction and the subsequent application and removal of a demagnetizing field H in the reverse direction. The relation between Mr(H) and Md(H) is then used to determine IGEC in magnetic materials. For an assembly of small non-interacting particles, Stoner–Wohlfarth theory shows
 |
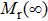
 |
To describe the reason of the positive value and peak of the δ m(H) curve, a system with two grains are considered, assuming that the magnetic reversal field is H0 for the two identical grains with easy axes are parallel to each other.[261] At the initial state, the magnetic moments are on the opposite directions in order to simulate the thermal demagnetized status. As the IGEC favors the parallel magnetic moments in order to reduce the exchange energy, an applied field (H1) smaller than H0 is then required to align the thermal demagnetized system. When a demagnetizing field is applied, the magnetic moments in both grains will not reverse until the field reaches H0, as IGEC does not play a role in the system already having minimum exchange energy. Therefore a δ m(H) curve, as shown in Fig. 
 | Fig. 50. δm(H) curve of a two-grain system.[261] |
Zhang et al.[262] and Rong et al.[261] studied the dependence of δ m(H) on microstructure characteristic of the nanocrystalline and nanocomposite magnet. Figure
 | Fig. 51. The plots of δm vs. H/Hc for the variation of (a) exchange constant and (b) anisotropy constant of the grain boundary layer.[262] |
The effective of Henkel plot could be verified by experiments. Here two examples are given to compare the Henkel plots, normalized remanence, hysteresis loops and therefore to correlate the Henkel plot and IGEC in the nanocomposite magnets.[263] Figure
 | Fig. 52. (color online) (a) δm plots of the samples compacted at 400 and 600 °C from the fcc FePt nanoparticles. (b) δm plots of the isolated L10 particles and samples compacted under 2.5 GPa at 200 °C as well as the post-annealed samples. The insets are the corresponding demagnetization curves.[263] |
The recoil loops represent the variations of working points in the application of permanent magnets, such as in a permanent magnet motor or generator. The enclosed area of the recoil loop means energy loss after one cycle. This energy is typically very small in sintered magnets. From the point view of material research, the recoil loops are measured by removing and re-applying a demagnetizing field to a magnetic material, as the demagnetizing field is increased successively. Recently researchers found that the recoil loops are quite open for nanocrystalline magnets, especially for nanocomposite magnets. Therefore, the recoil loop measurements are also often used to characterize the IGEC in nanocrystalline magnetic materials.
Physically, the open recoil loops can be composed of a time-dependent component and a time-independent one. The time-dependent component is contributed by magnetic viscosity, i.e., thermal relaxation/fluctuation. The time-independent component is majorly contributed from the IGEC, especially for the single-phase nanocrystalline magnets as the energy barrier for the magnetic reversal in the magnetically hard phase is quite large. Both components are discussed below.
Rong et al. studied the effect of thermal fluctuation on the recoil openness of an exchange-coupled FePt/Fe3Pt nanocomposite system with well-defined magnetically hard/soft two-phase morphology, which was prepared by reducing reaction of chemically synthesized FePt/Fe3O4 bimagnetic nanoparticles.[265] TEM analysis shows that the grain size of 650 °C annealed sample is only 8–13 nm, while serious grain growth was observed in the 800 °C annealed sample. In addition, both magnetically hard L10-FePt phase and magnetically soft phase Fe3Pt exist in the 650 °C annealed sample, while only single phase L10-FePt is found in the 800 °C annealed sample. XRD analysis confirms that the volume fraction of the Fe3Pt phase decreases from 28 ± 3% to 8 ± 2% with increasing annealing temperature from 500 to 650 °C. The recoil loops were then measured with different sweep rate (η) of applied magnetic field from η = η0 to 

 | Fig. 53. (color online) Recoil loops of the (a) 550 and (b) 800 °C annealed samples with different sweep rates: (black) η = η0 and (red) 

|
To analyze the relation between the recoil loop openness and the thermal fluctuation quantitatively, two different methods were used to measure the activation volume, i.e., the sweep-rate dependence of the coercivity, and magnetic viscosity measurements. The activation volumes obtained by these two methods are quite similar. Figure 






 | Fig. 54. (color online) (a) The dependence of coercivity on sweep rate for different samples. The inset gives the dependence of 

|
The correlation between the recoil loop openness and thermal fluctuation can be understood as follows: in a hard/soft nanocomposite, the magnetic moments in the soft phase are exchange coupled by the magnetically hard grains, while they tend to be unstable under a moderate reverse field and are easy to thermally reverse, especially for those in the center of soft grains due to the lower energy barrier compared to those near the hard phase.[15] The unstable moments are then affected sensitively by thermal fluctuation and contribute to the large openness in the recoil loops of the nanocomposite magnets. Larger openness is normally observed in the recoil loops of nanocomposite magnets compared with single-phase magnets since the magnetic moments in the soft phase of nanocomposites are more unstable than those in grain boundary regions in single-phase hard magnets.
While thermal fluctuation does contribute to the recoil loop openness as discussed above, it is not the only major factor, as one still see the open recoil loop in single-phase nanocrystalline magnets. Here the micromagnetic FEA simulation is used to investigate the origin of recoil loop openness in exchange-coupled nanocrystalline magnets where the thermal fluctuation is not considered.[267] An isotropic single-phase magnet was constructed by assembling of 64 cubic Nd2Fe14B grains with random orientation, as shown in the inset of Fig.
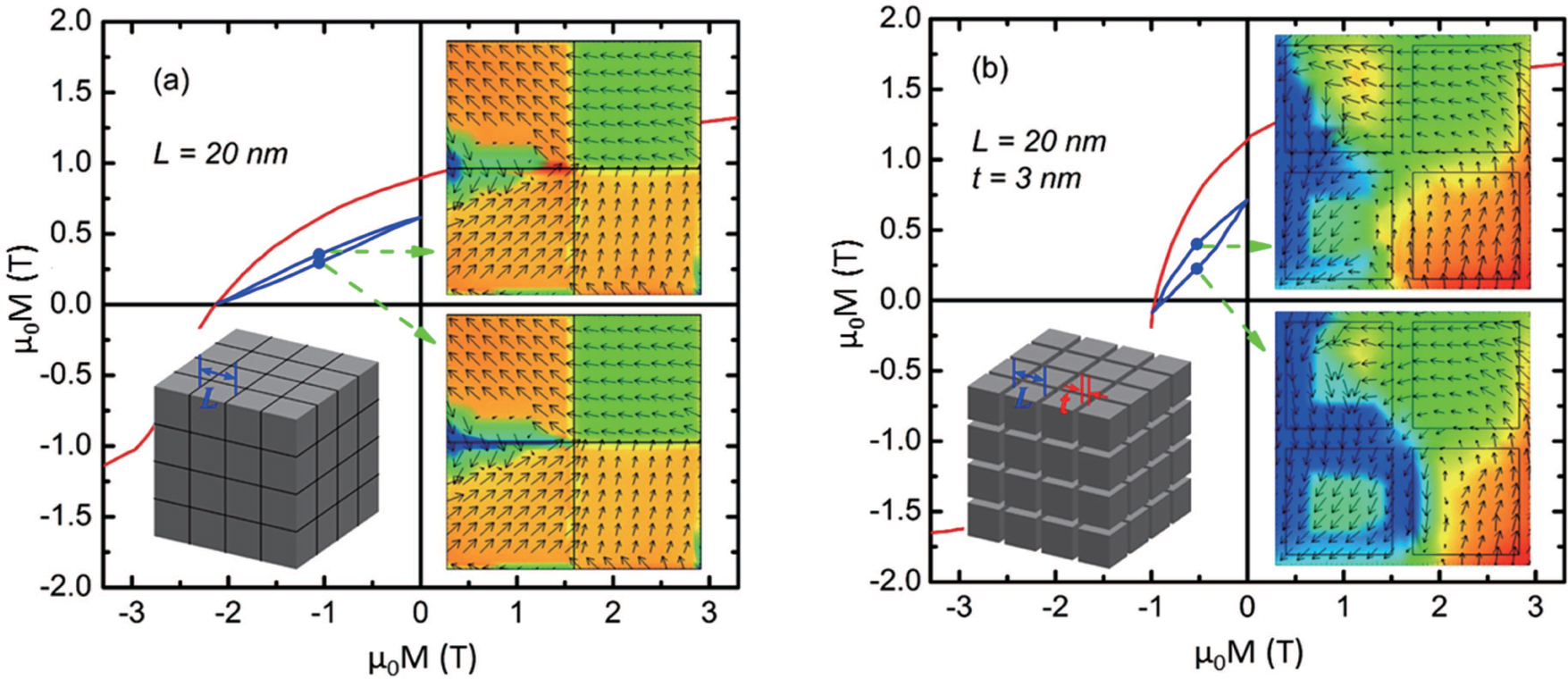 | Fig. 55. (color online) The recoil loops with maximum openness of (a) the single-phase magnet with L = 20 nm and (b) the nanocomposite magnet with L = 20 nm and t = 3 nm. The insets shown in the third quadrant are the 3D model of single-phase and hard-soft phase nanocomposite magnets. The insets in the right side give the magnetization distributions at different magnetic history, i.e., upper and lower branches of recoil loop under field 
|
Figure
 | Fig. 56. (color online) The dependence of 
|
Since the intergrain exchange coupling either between the grains in the same phase or different phases always leads to the deviation of magnetic moments in grain boundary regions from easy-axis directions of the grains in order to reduce the exchange energy and thus system Gibbs free energy, it is natural to assume that the exchange energy distribution over a nanocrystalline is related to the origin of open recoil loops. Figures
The origin of an open recoil loop can be better understood by comparing the magnetization distributions in the single-phase and nanocomposite magnets, as shown in the insets of Fig.
In summary, the open recoil loops in the nanocrystalline and nanocomposite magnets are majorly caused by the IGEC and thermal fluctuation. Zheng et al. reported similar micromagnetic simulation and also attributed the open recoil loop to the strong intergrain exchange coupling, which results in the magnetization reversal in some hard grains during the recoil processes.[268] The chance of the magnetization reversal in magnetically soft grains is larger, leading to a larger of recoil loops of the nanocomposite magnets. On the other hand, Li et al. confirmed the dependence of recoil loop openness on the sweep rate of magnetic field, the correlation between the recoil loop openness, activation volume and reversible susceptibility.[269]
Although the magnetic characterization of materials is usually made by measuring a hysteresis loop, it is not possible to obtain information of interactions or coercivity distributions from the hysteresis loop solely. First-order-reversal-curves (FORC) provide insight into the relative proportions of reversible and irreversible components of the magnetization of a material. In addition, the magnetostatic and exchange interactions between the magnetically hard and soft phases can be mapped using FORC diagrams for the exchange-coupled magnets. An FORC measurement begins by saturating the samples with a large positive applied field. The field is decreased to a reversal field, and then the FORC is defined as the magnetization curve measured with increasing applied field back to saturation. The measurement procedure is repeated for different values of reversal fields to obtain a suite of FORCs and a two-dimensional distribution function. The FORC diagram is defined as the mixed second derivative of the applied field and the reversal field. A detailed description of FORC distribution can be found in Refs. [270] and [271].
Rong et al. studied the correlation between FORC diagrams and the microstructure of the SmCo5/α-Fe nanocomposites,[272] which are the same samples shown in Fig.
There is only one major peak around the origin for the un-milled sample since both the raw α-Fe and SmCo5 powders have near zero coercivity. No useful information could be detected for this case.
Ball milling reduces the grain size while post-annealing restores the crystallinity for the SmCo5 phase, which in turn raises the coercivity. As a result, there are two completely separated peaks along the bias axis for the sample milled for 30 minutes, one near origin and one near 15 kOe, which represent the magnetization reversals of the magnetically soft and hard phases, respectively. The separated magnetization reversal indicates weak exchange interaction between the two magnetic phases. A distinct ridge is observed at an angle of ∼135° across the lower half of the FORC diagram, which could be attributed to the magnetostatic interaction between the magnetically soft and hard phases.
The two peaks along the bias axis merge when milling time is increased to 60 minutes, which is attributed to the grain refinement of α-Fe phase. The magnetic moments in the α-Fe grains are partially exchange-coupled and thus the switching field of the magnetically soft phase increases. However, a large amount of α-Fe phase is still in a form of strips and not exchanged coupled, therefore there is still a strong peak around the origin in the FORC diagram. The ridge around ∼135° becomes weak with increasing milling time since the exchange interaction starts to dominate the magnetization behavior with grain refinement.
Extending milling time leads to further grain refinement and homogeneously distributed α-Fe grains are obtained when the milling time is longer than 4 hours. The soft phase is completely exchange-coupled and thus there is only one major peak in the FORC diagram around 
 | Fig. 57. (color online) The 2D and 3D FORC diagrams of the samples (a) without milling, and milled for (b) 30, (c) 60, and (d) 240 minutes after annealing at 525 °C for 30 minutes. Left column is the colored FORC curves with the FORC distribution plotted inside the hysteresis loop. The middle column is the 2D FORC diagrams and right column is 3D FORC diagrams.[272] |
Based on the analysis of FORC diagrams and microstructures, it is found that FORC can provide deeper information on the magnetic interactions inside of exchange-coupled magnets than the simple hysteresis loop, remanence enhancement and even Henkel plot, although the measurements of FORC diagram is usually time-consuming.
Coercivity is one of the most important extrinsic parameters that characterizes permanent magnets, since it reflects the ability of the magnet to resist magnetization reversal under the application of an external field. For conventional sintered magnets, the coercivity mechanisms are dominant by either nucleation-type or domain-wall pinning-type. In nucleation-type magnets, such as Nd2Fe14B, SmCo5, or hard ferrite sintered magnets, the magnetic domain walls can move easily within the grains, so that the magnetization increases steeply even in small magnetizing fields for a thermal demagnetized magnet. However, a large demagnetizing field is required in order to form the nuclei of reversed domain in every saturated grain during demagnetizing process. In pinning-type magnets, the magnetic domain walls are pinned at phase boundaries, precipitates, or planar crystal defects, for instance, in Sm(CoCuFeZr)z sintered magnets. In order to saturate or demagnetize a pinning-type magnet, the domain walls must be removed from the pinning sites, which requires magnetizing fields larger than the pinning field strength. Therefore, a large magnetic field has to be applied in order to overcome the pinning force for both magnetizing and demagnetizing processes. The initial or virgin magnetizing curve of a magnetic material from the thermally demagnetized state indicates which coercivity mechanism prevails, as shown in Fig.
 | Fig. 58. (color online) Virgin magnetizing curves of typical nucleation-type and pinning-type sintered permanent magnets. |
The general equation that proved to be applicable to a vast majority of hard-magnetic materials presents the coercivity as
 |
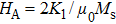

 |
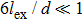


 |
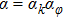
 | Fig. 59. (color online) Normalized coercivity (
|
Magnetization reversal includes reversible and irreversible processes in nature. Irreversible processes are characterized by a free energy barrier which can only be overcome by increasing the applied field or through thermal activation. Reversible magnetization processes, on the other hand, do not require a critical field for initiation. The reversible magnetization is back to its original status after the applied field is removed. The reversible susceptibility can be determined at any point along a magnetization curve by the measurement of a minor loop associated with a small reversing field increment, Δ H. The slope of the minor loop, Δ M/Δ H is defined as the incremental susceptibility and, in the limit of 

In nanocomposite magnets, reversible magnetization mainly originates from the effect of exchange coupling especially in the magnetically soft component, and irreversible magnetization results from magnetization reversal in magnetically hard grains. Therefore, the reversible or irreversible susceptibilities can be used to investigate the intergrain exchange coupling. Li et al. compares the reversible and irreversible susceptibilities of the under-quenched, optimal and over-quenched nanocomposite Pr9Fe85.5B5.5 magnets which are melt-spun at 20.5, 21.5, and 23 m/s, respectively.[285] The grain size of Pr2Fe14B is 21.9, 17.5, and 16.8 nm and that of α-Fe is 18.7, 16.4, and 15.3 nm, respectively. Figure 
 | Fig. 60. (color online) The reversible susceptibility χrev/Ms vs the applied field at room temperature for the Pr9Fe85.5B5.5 nanocomposite ribbons melt-spun at (A) 20.5, (B) 21.5, and (C) 23 m/s. The inset shows irreversible susceptibility χirr/Ms vs the applied field.[285] |
The relationship between reversible and irreversible magnetizations can be used to distinguish the magnetic hardening mechanism of permanent magnets, which was proposed and applied to both Sm(CoCuFeZr)z and NdFeB magnets by Crew et al..[286–288] Rong et al. applied this method to analyze the coercivity mechanism of the Sm(CoCuFeZr)z melt-spun ribbons.[289,290] Figure 

The developments of single-phase nanocrystalline and nanocomposite magnets prepared by melt spinning technique have been reviewed in this article. Although partially crystallographic texture can be developed in the melt-spun ribbons with special controls on the process and composition, most nanocrystalline and nanocomposite are isotropic, which limits the energy product to ∼25 MGOe. While the concept of exchange coupling has been widely accepted, the magnetic phenomena in the nanocrystalline and nanocomposite magnets are not understood thoroughly. With the hot deformation of the single-phase melt-spun ribbons, desired texture could be developed in the magnets with an energy product approaching to ∼50 MGOe. However, no sufficient magnetically soft phase can be implanted into the magnetically hard phase matrix in order to form an anisotropic nanocomposite magnet with enhanced magnetic properties. Further studies are still required to understand the correlations between exchange coupling, thermal activation, and magnetic reversal in order to guide the future magnet design.
Although attempts to fabricate anisotropic nanocomposite bulk magnets have been made via hot deformation of the (Nd, Pr, Dy)2Fe14B/α-Fe nanocomposite materials, the energy product is still low.[291] Future success on the anisotropic nanocomposite magnets may be established on different technologies, but the main ideas are to align the magnetically hard phase and possibly increase the content of magnetically soft phase, while neither of them is technically easy. On the other hand, magnets with low cost always attract attention especially for industrial applications. Therefore, cheap RE-substituted magnets and even RE-free magnets should be a research topic as long as a trade-off on the magnetic properties is acceptable.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] | |
| [136] | |
| [137] | |
| [138] | |
| [139] | |
| [140] | |
| [141] | |
| [142] | |
| [143] | |
| [144] | |
| [145] | |
| [146] | |
| [147] | |
| [148] | |
| [149] | |
| [150] | |
| [151] | |
| [152] | |
| [153] | |
| [154] | |
| [155] | |
| [156] | |
| [157] | |
| [158] | |
| [159] | |
| [160] | |
| [161] | |
| [162] | |
| [163] | |
| [164] | |
| [165] | |
| [166] | |
| [167] | |
| [168] | |
| [169] | |
| [170] | |
| [171] | |
| [172] | |
| [173] | |
| [174] | |
| [175] | |
| [176] | |
| [177] | |
| [178] | |
| [179] | |
| [180] | |
| [181] | |
| [182] | |
| [183] | |
| [184] | |
| [185] | |
| [186] | |
| [187] | |
| [188] | |
| [189] | |
| [190] | |
| [191] | |
| [192] | |
| [193] | |
| [194] | |
| [195] | |
| [196] | |
| [197] | |
| [198] | |
| [199] | |
| [200] | |
| [201] | |
| [202] | |
| [203] | |
| [204] | |
| [205] | |
| [206] | |
| [207] | |
| [208] | |
| [209] | |
| [210] | |
| [211] | |
| [212] | |
| [213] | |
| [214] | |
| [215] | |
| [216] | |
| [217] | |
| [218] | |
| [219] | |
| [220] | |
| [221] | |
| [222] | |
| [223] | |
| [224] | |
| [225] | |
| [226] | |
| [227] | |
| [228] | |
| [229] | |
| [230] | |
| [231] | |
| [232] | |
| [233] | |
| [234] | |
| [235] | |
| [236] | |
| [237] | |
| [238] | |
| [239] | |
| [240] | |
| [241] | |
| [242] | |
| [243] | |
| [244] | |
| [245] | |
| [246] | |
| [247] | |
| [248] | |
| [249] | |
| [250] | |
| [251] | |
| [252] | |
| [253] | |
| [254] | |
| [255] | |
| [256] | |
| [257] | |
| [258] | |
| [259] | |
| [260] | |
| [261] | |
| [262] | |
| [263] | |
| [264] | |
| [265] | |
| [266] | |
| [267] | |
| [268] | |
| [269] | |
| [270] | |
| [271] | |
| [272] | |
| [273] | |
| [274] | |
| [275] | |
| [276] | |
| [277] | |
| [278] | |
| [279] | |
| [280] | |
| [281] | |
| [282] | |
| [283] | |
| [284] | |
| [285] | |
| [286] | |
| [287] | |
| [288] | |
| [289] | |
| [290] | |
| [291] |