† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51265019).
Through the first principles calculations, the chemical stability, mechanical, and electronic properties of chromium silicides are predicted. Estimating enthalpies and binding energies, density state density and electron density distribution are combined to analyse the thermodynamic stability and physical properties of chrome-silicon binary compounds. The chromium silicide includes Cr3Si, Cr5Si3, CrSi, and CrSi2. The chemical stability and the information about electronic structure, mechanical properties, Debye temperature, and anisotropy properties are obtained by density functional theory and Debye quasi-harmonic approximation. Meanwhile, the calculation of elastic modulus shows that Cr3Si has the highest body modulus value (251 GPa) and CrSi2 possesses the highest shear modulus (169.5 GPa) and Young’s modulus (394.9 GPa). In addition, the Debye temperature and the speed of sound of these Cr–Si compounds are also calculated. Since the calculated bulk modulus is different from Young’s modulus anisotropy index, and also different from Young’s modulus of a three-dimensional surface shape, the different mechanical anisotropies of all the compounds are obtained.
Transition metal silicides possess the characteristics of a high melting point, outstanding resistance to high temperature oxidation, high creep strength, excellent mechanical properties, and chemical stability. Therefore, they can be used in high-temperature structures.[1–3]
Researchers have shown great interest in transition metal silicides such as Cr–Si alloy compounds including Cr3Si, Cr5Si3, CrSi, and CrSi2. Yeh et al. fabricated a chrome-silicon alloy for coating the metal surface by self-propagating high-temperature synthesis.[4] Wang et al. prepared a chrome-silicon alloy using a water-cooled copper mold laser furnace, investigated microstructure characteristics, and discussed the formation mechanism of the phases in the Cr–Si alloy.[5,6] Kong et al. revealed the crystal structures of Cr–Si compounds by combining experimental measurements and density functional theory calculation. Schuster et al.[7,8] proposed a new thermodynamic description of the Cr–Si binary system. Krijn et al.[9] calculated the electronic structure and optical properties of Cr2Si according to the first principles, which are basically consistent with the experimental results. However, the mechanical properties, electronic properties and elastic anisotropy of Cr–Si compounds have not been studied systematically, owing to the difficulty in performing their syntheses and characterizations.
In this paper, the stability, chemical bonding properties, mechanical properties, and Debye temperature of chromium-silicon compounds are systematically studied by using the first-principles calculation. The work will be helpful in choosing reinforcing phases in the materials for aerospace industry or high temperature wear resistant materials.
All of the theoretical calculations in this paper were based on density functional theory (DFT) in the Cambridge Sequential Almighty Package (CASTEP) program.[10,11] For setting up crystal structure models of the Cr–Si compounds correctly, optimization of the models was carried out by using the planar wave expansion method, and the interaction between the atom core and valence electrons was achieved by using the ultra-soft pseudo-potential. For Cr and Si atoms, the electronic states Cr: 3s23p63d54s1 and Si: 3s23p2 were treated as valence states. Perdew et al. calculated the compound variation and related functions by a generalized gradient approximation.[12]
As shown in Fig.
 | Fig. 1. Cr–Si equilibrium phase diagram.[13] |
In order to study the thermodynamic stability of Cr–Si binary compounds, their enthalpies of formation and cohesion are calculated and the two energy formulas are defined as follows:


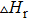
Table
 | Fig. 3. (color online) Plots of calculated cohesive energy and formation energy versus Si content of Cr–Si compounds. |
| Table 1.
Calculated parameters (a, b, c in unit Å), cohesive energy (eV/atom), and formation enthalpy (eV/atom) of Cr–Si compounds. . |
According to the order of the formation enthalpy and the bonding energy of the Cr–Si compounds, the order of thermal stability of Cr–Si compounds is 
In order to analyze the chemical bond properties of chrome-silicon compounds and the electron density distribution of the electronic structure, the total state of atoms (TDOS) and the partial state of charge (PDOS) are shown in Fig.
 | Fig. 4. (color online) Plots of calculated total density of states (TDOS) and partial density of states (PDOS)versus energy for the Fe and Cr–Si system. Dashed line represents the Fermi level. |
The nature of the magnetic characteristic can be understood from the spin-polarized total density of states. Generally speaking, the up and down states are symmetric, but the up and down states of CrSi are dissymmetric, which indicates the magnetic characteristic.[26,27] Actually, the low and high valence bands are almost symmetric, and the up and down states are dissymmetric with respect to the Fermi level but very close to the Fermi level. Comparing with other compounds, we can guess they have no magnetic characteristics, because the down and up states are symmetric.
The electron density values are greatly larger than zero even in the interstitial regions, which presents the strong metallic characteristic of Cr–Si compounds.[28,29] For all chromium silicides, the d band of Cr dominates the total state density, because the variation of d bond corresponds most to the total state density. Their Fermi level lies at the shoulder of the TDOS peak, which means that they are all stable. It is consistent with the results of binding energies and formation enthalpy.
Mulliken population analysis is one parameter to reveal the material interior chemical bonding characteristics. The average bonding length and average population can be calculated from the following equations:[30]



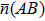
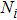

| Table 2.
Population analysis results of the studied Cr–Si compounds: Total refers to electron occupation; Charge denotes electron transition; |
From Fig.
Figure
Based on the generalized Hook law, the elastic constants of Cr–Si compounds are calculated by using the stress-strain method. The structure of the crystal is calculated by several different strain modes, and the corresponding Cauchy stress tensor is evaluated.
According to these strain–stress relationships in Eq. (

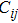
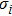
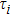
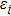
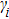
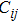
The calculated elastic constants of the Cr–Si system are summarized in Table
For cubic system (for Cr3Si, CrSi):



From Table 






| Table 3.
Calculated elastic constants (in unit GPa) of Cr–Si compounds. . |
The bulk modulus (B), shear modulus (G), Young’s modulus (E), and Poisson’s ratio (σ) are calculated using Eqs. (




| Table 4.
Calculated bulk moduli, shear moduli, Young’s moduli, and Poisson’s ratios of CrSi compounds. . |
In order to depict the mechanical properties of the Cr–B binary compounds, the elastic constant curves with the change of Si content are listed in Figs. 


 | Fig. 6. (color online) Variations of bulk modulus, shear modulus, and  |
The specific heat, elastic constant, melting point, and chemical bonding properties of the compound can be reflected by the Debye temperature.[44] In this subsection, Debye temperature (HD) and average sound velocity (vm) can be described by the following relations:[31,45,46]




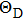
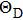
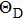
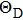
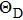
 | Fig. 8. (color online) Variations of Poisson’s ratio and Debye temperature with Si content of Cr–B binary compounds. |
| Table 5.
Theoretical density (ρ in unit |
The mechanical anisotropy is essential in the applications of Cr–Si materials. Micro cracks form not only on the surface, but also inside of the material. The formation and propagation of micro cracks relate to anisotropy. Cr–Si compounds act as one of the structural materials used in elevated temperature, and their mechanical anisotropy must be investigated. The following equations are combined to describe the degree of anisotropy, a number of parameters, including the anisotropic index 











Table 














| Table 6.
Calculated values of universal anisotropic index ( |
Young’s modulus curved surface of three-dimensions (3D) would explain why the anisotropic properties are so much simpler. The Young modulus is calculated on the basis of the following formulas:[51–53]
for the cubic crystal (for Cr3Si, CrSi):


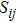

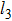
 | Fig. 10. (color online) Planar projections of Young’s modulus of the Cr–Si compounds on (100), (001), and (110) crystallographic planes. |
Moreover, in the [010] and [100] directions, the Cr3Si exhibits the maximum value of Young’s modulus, and Cr5Si3 shows the smallest Young’s modulus on the (001) plane. In addition, the largest values of Young’s modulus for Cr5Si3 and CrSi2 deviate from their principal axes at the (110) plane. In addition, it is found that the CrSi shows the smallest Young’s modulus in the [010] and [100] directions on the (001) plane. On the (001) and (110) planes, the planar contours of CrSi2 seems to be a spherical shape, which means that the Young modulus of CrSi2 has a weaker anisotropy than other compounds’.
The first-principle calculations, including the chemical stability, electronic structures, Debye temperature, and anisotropic properties are combined to investigate the properties of Cr–Si binary compounds. The calculated cohesive energy and formation enthalpy indicate the thermodynamical stability. From the electronic structures of the Cr–Si binary compounds, we deduce that the bonding characteristics are determined by Cr–Si covalent bonds, but also possess the metallic character. In particular, the CrSi2 has stronger covalent bond properties than other silicides. The results show that the Cr3Si has the highest value (251.0 GPa) of bulk modulus and the CrSi2 has the highest values (169.5 GPa and 394.9 GPa) of shear modulus and Young’s modulus, respectively. The value of Debye temperature indicates the strong covalent bonds of the Cr–Si compounds. The CrSi2 has the largest Debye temperature (262.0 K), indicating stronger covalent bonds characters than others. To verify the mechanical anisotropy, the Young modulus of the Cr–Si binary compound is plotted by the 3D surface contour.
The authors thank those people for their scientific contributions to this work.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] |






































