† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61372034).
Circularly polarized (CP) lens antenna has been applied to numerous wireless communication systems based on its unique advantages such as high antenna gain, low manufacturing cost, especially stable data transmission between the transmitter and the receiver. Unfortunately, current available CP lens antennas mostly suffer from high profile, low aperture efficiency as well as complex design. In this paper, we propose an ultra-thin CP lens antenna based on the designed single-layered Pancharatnam–Berry (PB) transparent metasurface with focusing property. The PB metasurface exhibits a high transmissivity, which ensures a high efficiency of the focusing property. Launched the metasurface with a CP patch antenna at its focal point, a low-profile lens antenna is simulated and measured. The experimental results show that our lens antenna exhibits a series of advantages including high radiation gain of 20.7 dB, aperture efficiency better than 41.3%, and also narrow half power beam width (HPBW) of 13° at about 14GHz. Our finding opens a door to realize ultra-thin transparent metasurface with other functionalities or at other working frequencies.
Metamaterials[1–5] and their planar version, metasurfaces (MS), have provided strong capabilities to manipulate the wavefronts of electromagnetic (EM) waves through their desirable control on local phases. As a result, a lot of fascinating effects are investigated, such as anomalous refraction/reflection,[6–8] planar focusing lens,[9,10] photonic spin Hall effects,[11] propagation wave to surface wave[12,13] and many other related functional metadevices.[14,15] Very recently, Pancharatnam–Berry (PB) MS[6,16,17] have been proposed and studied to control circularly polarized (CP) waves in an effective way. Many multi-functional meta-devices have been designed by combining two sets of functional units, including bifunctional holograms[18] and multiplexing vortex beams.[19,20] However, the efficiencies of transmission-mode PB MS are typically very low because of the large specular modes. In practice, transmission geometry is more useful. Therefore, how to design a high-efficiency transmissive PB metasurface remains as a great challenge.
As one of the most important aspects, MS have been used to improve antenna performances. For example, primary antennas are engineered with a significant directivity enhancement by loading a multilayer focusing MS.[21–23] Four-beam antennas are also engineered by introducing phase-optimized MS.[24] However, the design of ultra-thin single-layered CP lens antenna has been reported rarely.
To solve these issues, in this paper, we propose a new strategy to improve the efficiency of transmissive PB MS by introducing anisotropic structures in a single-layered element. The simulated transmission amplitude reaches more than 0.9 for our designed element at its center frequency 14 GHz. To practically demonstrate the high efficiency of the proposed element, we design an ultra-thin transparent lens with a focal length of 40 mm. Excited by a well-optimized right hand circularly polarized (RHCP) patch antenna at the focal spot, a CP lens antenna is engineered and measured. Our study is useful to design other wave-manipulated meta-devices with high efficiencies.
In order to provide a full control of the wave front, it is of great importance to obtain a complete phase variation in the whole range from 0 to 2π, while sustaining equal amplitude. Based on the PB theory,[6] we can manipulate the phase profile by rotating the structures while maintain a consistent amplitude information. An early theoretical study has claimed that working efficiency is bounded by 25% in transmissive ultra-thin MS.[25] Zhou[26] adopts an ABA transparent system to improve the efficiency and the experimental result is better than 90%. However, the structures are complex and suffer from a multilayer system. Therefore, we propose a single-layered PB cell, which eliminates the drawbacks of multilayer.
As we know, a RHCP wave propagating along the +z direction and its transmitted waves can be described as follows:
 |
 |
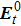
 |
Supposing tx = ty = t and Φy = Φx + π, the transmission wave passing through the element rotated with angle of φ can be described as
 |
 |
Figure
 | Fig. 1. (color online) Design and simulation of the element. (a) The structure of the element and (b) perspective view of the simulation setup. |
To figure out the performance of the element, figures
 | Fig. 2. (color online) The simulated (a) transmissivity and (b) phase shift of x-polarized and y-polarized plane waves. |
Figure
 | Fig. 3. (color online) (a) S parameters of the element under illumination of normally incident RCP wave. (b) phase shift of the element under different rotation angle. |
To understand the transmission performance of the element under oblique incidence, figure
With the well-optimized element in hand, we can design many functional meta-devices by manipulating the local phases of MS. Here, a focusing lens is designed for example. To achieve the goal of mentioned meta-lens, we require that the phase functions Φ(x, y) should satisfy the following parabolic distribution
 |
 |
To give an insight into the focusing effect, we calculate and depict the power distributions along the measured line1 on xoz plane and measured line 2 on xoy plane shown in Fig.
We can learn from the previous section that the designed meta-lens is capable of focusing a plane wave to a spot effectively. Based on the reciprocity of EM wave propagation, the meta-lens can also be employed to design CP antenna by converting the spherical wave emitted from the focal point into a plane wave. Thus, a CP patch antenna operating near 14 GHz is needed to act as the feed source. The CP patch antenna exhibits a 3-dB axial ratio (AR) bandwidth of 13.4 GHz–14.3 GHz, within which the antenna has a good impedance match property. By placing the patch antenna at the focal spot of the designed meta-lens, the CP lens antenna is designed with the structural configurations shown in Fig.
In order to verify the simulation, the MS and patch antenna are fabricated with their pictures shown in Fig.
 | Fig. 9. (color online) Fabricated picture and measurement schematic of lens antenna. (a) Fabricated picture for MS and RCP antenna, (b) schematics of the far-field measurement. |
Figures
 | Fig. 10. (color online) Measured and simulated far-field radiation patterns in (a) xoz-plane (b) yoz-plane. Broadband performance of (c) gain and AR and (d) aperture efficiency. |
| Table 1. Comparison with previous work . |
In this paper, an ultra-thin CP lens antenna based on single-layered transparent metasurface is proposed, fabricated and measured. The MS consists of 15×15 cells with thickness of 0.07 λ0 and takes up an area of 102 mm × 102 mm with F/D = 0.39. By placing an RCP radiating source at the focal point to launch the lens antenna, the quasi-spherical waves emitted from the patch antenna are efficiently transformed into plane waves, resulting in a high gain radiation in far field. The ultra-thin CP lens antenna achieves good radiation performances in terms of measured gain of 20.7 dB, aperture efficiency of 41.3%, HPBW of 13° at 14 GHz. Furthermore, the lens antenna effectively operates in the spectrum of 13.4 GHz–14.6 GHz. With improvements in efficiency, bandwidth, profile and layers reduction, our design may provide a promising approach to planar and integrate high gain CP antennas in wireless communication systems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |







