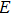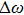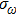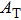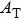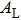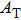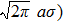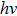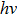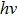† Corresponding author. E-mail:
Project partially supported by the Research Grant Council of Hong Kong, China (Grant No. RGC 660207) and the Macro-Science Program, Hong Kong University of Science and Technology, China (Grant No. DCC 00/01.SC01).
The discovery of the Planck relation is generally regarded as the starting point of quantum physics. Planck’s constant h is now regarded as one of the most important universal constants. The physical nature of h, however, has not been well understood. It was originally suggested as a fitting constant to explain the black-body radiation. Although Planck had proposed a theoretical justification of h, he was never satisfied with that. To solve this outstanding problem, we use the Maxwell theory to directly calculate the energy and momentum of a radiation wave packet. We find that the energy of the wave packet is indeed proportional to its oscillation frequency. This allows us to derive the value of Planck’s constant. Furthermore, we show that the emission and transmission of a photon follows the all-or-none principle. The “strength” of the wave packet can be characterized by ζ, which represents the integrated strength of the vector potential along a transverse axis. We reason that ζ should have a fixed cut-off value for all photons. Our results suggest that a wave packet can behave like a particle. This offers a simple explanation to the recent satellite observations that the cosmic microwave background follows closely the black-body radiation as predicted by Planck’s law.
The birth of quantum mechanics is commonly attributed to the discovery of the Planck relation. In order to explain black-body radiation, Planck postulated that the radiation energy is transmitted in packages (“energy quanta”). Einstein later studied the photoelectric effect and found that the energy of light absorbed by an electron is also in small “packets”, which, like Planck’s “energy quanta”, is proportional to the light frequency ν.[1] This relation is now called the Planck relation or Planck–Einstein relation:
 |
The constant “h” here is called “Planck’s constant”. Subsequently, Planck’s constant was found to play a major role in many aspects of quantum physics, including the de Broglie relation p = hk; Dirac’s fundamental quantum condition: 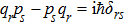

Investigating the physical origin of Planck’s constant is not only important for advancing our understanding of the foundation of quantum physics, but also relevant to the current study of cosmology. According to the Big Bang theory,[5] in the early day of the universe, it was filled with energetic photons. After the universe cooled down, these primordial photons became the cosmic microwave background (CMB) that we can detect today.[6] From the recent satellite measurements, the microwave detected in the CMB follows perfectly Planck’s law of black-body radiation.[7] Thus, the microwave radiation must obey 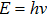
It is obvious that the microwave is a wave packet of electromagnetic radiation. It cannot be regarded as a pointed object, since its wave length is quite long. Then, how is it explained that CMB satisfies Planck’s relation? We think the answer is that a particle does not need to be a pointed object; a wave packet can behave like a particle. This work is to show that this can be the case.

When the concept of h was first proposed in 1900, Planck thought that the idea of energy quantization was “a purely formal assumption ⋯ actually I did not think much about it ⋯”.[8] Later, he tried to justify Planck’s relation by using a very complicated theoretical argument, which was hidden in cumbersome formulism of thermodynamics and statistical mechanics.[9] A more comprehensible treatment of Planck’s argument was put forward by Debye in 1910.[9,10] In the following, we will briefly review Planck’s derivation of h by using Debye’s cleaned-up version as outlined by John Slater.[9]
Planck’s theory was basically to treat the emitter in the black-body radiation as a linear oscillator,
 |
Here, E, T, and V represent the total energy, kinetic energy, and potential energy, respectively; q is the generalized coordinate and p is the generalized momentum; m and ω are the mass and frequency of the oscillator. If one maps the energy distribution in the phase space, one will find that the contour of a constant energy is an ellipse (Fig.
 |
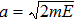
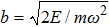
 |
Then, when the energy is increased from E to 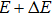
 |
Planck then made two formal assumptions:
With the above assumption, one can calculate the average energy of a black-body radiation emitter oscillating at frequency v by using the Boltzmann distribution, that is,
 |
For simplicity, we denote 
 |
We know
 |
 |
Therefore,
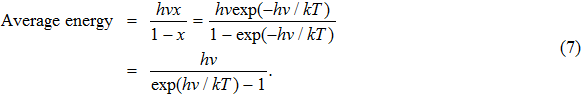 |
Since we know that the number of energy states per unit volume and per unit frequency range in the radiation field is 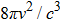
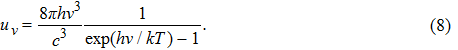 |
This equation is now known as “Planck’s law”. It fitted the experimental data of black-body radiation very well.[11]
Although the Planck law was a great success, Planck was not satisfied with the physical meaning of h as he derived it. Particularly, he knew that the assumption of partitioning the phase space (of the oscillator) into equal incremental areas is somewhat arbitrary. Planck spent subsequent years trying to justify his theory on better physical grounds but was not successful.[9]
In this paper, we try to uncover the physical meaning of h by treating the photon as a wave packet of electro–magnetic radiation and directly calculating the total energy and momentum contained within the wave packet. More explicitly, the approach of this study is based on the following steps:
The energy density of an electro–magnetic field is known to be[12]
 |
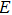


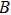
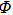

 | (10a) |
 | (10b) |
In electro–magnetic radiation, the vector potential 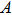
 |
In order to calculate the energy density of an electro–magnetic wave, we choose a simple system in which the wave travels along the z axis and the vector potential is along the x axis (see Fig. 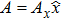
 |
Since there is no embedded charge within the vacuum, 
 | (13a) |
 | (13b) |
Substituting Eqs. (
 |
This relation suggests that Ax plays the role of the “field parameter” in wave propagation. This point can be easily seen by comparing Eq. (
 |
Here ρ is the mass density of the string, and F1 is the tension of the string.[13] One can immediately see that in the electro–magnetic system, Ax appears to play the role of a propagating field, just like the displacement ϕ in the stretched string.
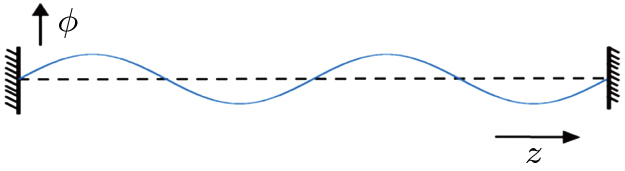 | Fig. 3. (color online) Wave propagation in a 1D stretched string. The wave travels along the z axis and ϕ is the local displacement of the string. |
Recall that the speed of light 
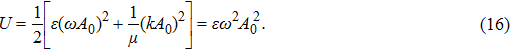 |
To find the physical meaning of Planck’s constant, we need to calculate the total energy 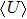
 |
In order to carry out this integration, one must know the structure of a photon. In the literature, a photon is usually described by Eq. (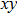
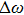

 |
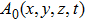
 |

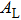
 |
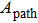

 |
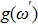
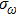
 |
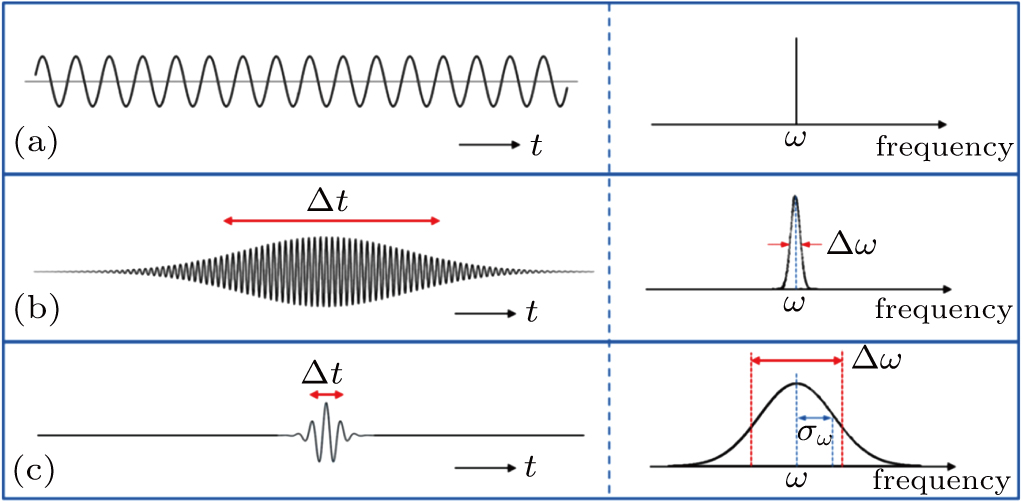
As is well known, the Fourier transform of Eq. (
 |
 |
Once we know the envelope function in the time domain, we can easily obtain the envelope function in the spatial domain along the z axis,
 |
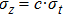
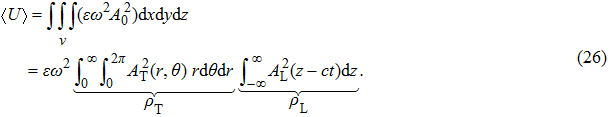 |
Here 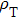

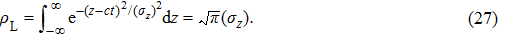 |
Recall that 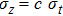

 |
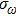

 |
In most transmitting media, the linewidth of a wave is proportional to frequency ω. This ratio is defined as the “Q factor”,
 |
The value of the Q factor is determined by the properties of the transmitting medium. Combining Eqs. (
 |
Substituting this into Eq. (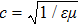
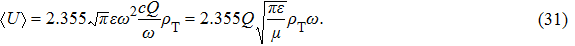 |
Next, we need to calculate the value of 

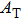

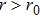
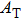
 |
 |
This is closely related to the area of integrating the transverse component 
 |
Combining Eqs. (
 |
Substituting Eq. (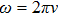
 |
Since 
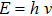
 |
We will show later that 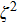
By treating the photon as a wave packet of electro–magnetic radiation, we can also calculate the total momentum contained within the wave packet. As is well known, the energy flow of the electro–magnetic field can be described by the Poynting vector 
 |
Since it can be shown that in a radiation system, 
 |
From Eq. (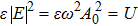
 | (39a) |
The total energy flux of a wave packet of electro–magnetic radiation then is
 |
For an electro–magnetic wave, the momentum density (
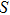
 |
Thus, the total momentum of a wave packet is
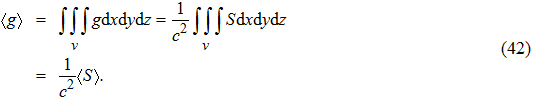 |
Substituting Eq. (
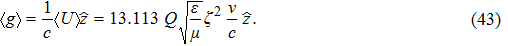 |
Previously, we have already identified the value of h from Eq. (
 |
Equation (
 |
Therefore, the Planck’s constant derived by us satisfies not only the Planck relation, but also the de Broglie relation.
In the foregoing sections, we demonstrate that one can directly calculate the energy of a photon based on Maxwell’s theory. Based on this result, the Planck constant is given by Eq. (
Apparently, the Planck constant is dependent on the physical properties of the vacuum, e.g., the dielectric permittivity ε and magnetic permeability μ. The quality factor Q is also a property of the vacuum, since it is dependent on the transmitting medium. At this point, we do not know enough about the detailed properties of the vacuum to directly calculate Q. But the value of Q can be determined experimentally. One can use an optical device to directly measure the linewidth of a photon with known frequency. In the literature, there were already some hints about the value of Q. For example, it was reported that a solid-state dye laser (at 590 nm) could have a linewidth around 350 MHz.[14] This suggests that the Q factor is about 1.45 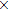
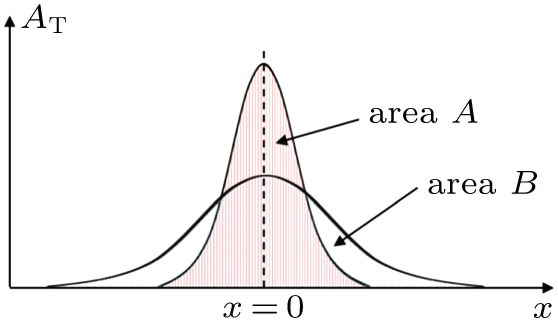
The remaining problem is to consider whether ζ2 can be regarded as a constant and what that means. From Eq. (
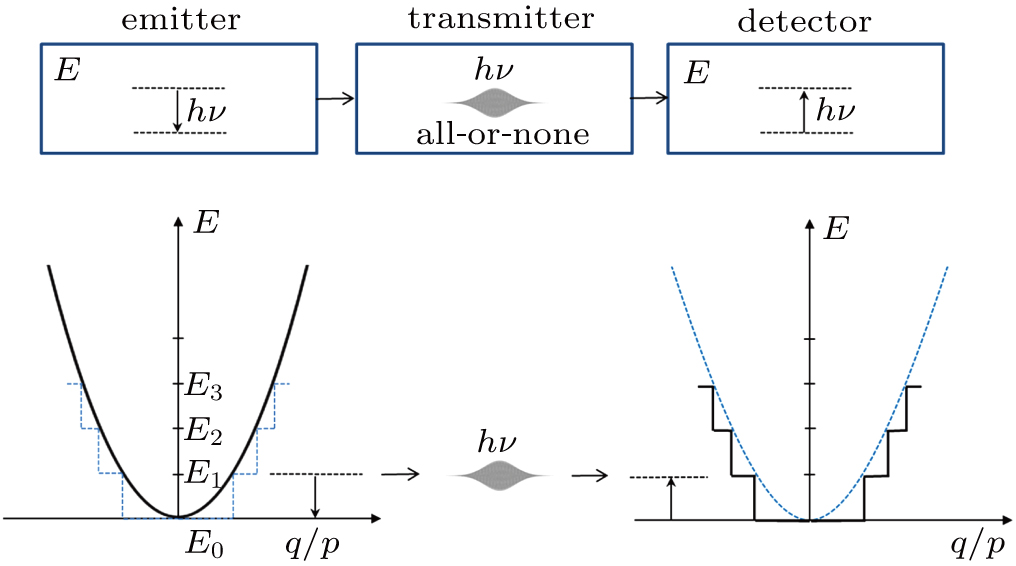
This situation is very similar to the generation of a nerve impulse. We know that a neuron can transmit a signal to its downstream target along its nerve fiber (called “axon”). This signal is called an “action potential”.[15] It is well known that the generation of action potential has the “all-or-none” property. That means that when the stimulus to the axon is below a threshold, no action potential can be generated. But when the stimulus is higher than the threshold, a full size action potential will be generated. This action potential will propagate along the axon with constant amplitude (about 100 mV).[16] In other words, one cannot generate an action potential with an arbitrarily small amplitude. And, no matter how large the stimulus is, one cannot generate an action potential which is much larger than 100 mV. That is why it is called “all-or-none”.
As it turns out, this all-or-none principle is applied in multiple aspects of nature. Not only the transmission of a nerve impulse is all-or-none, the transmission of the electro–magnetic radiation is also all-or-none. The radiation energy is apparently transmitted in small packets (photon), each of which has a limited size and is not sub-dividable. One can generate either a full size photon, or no photon at all. In other words, if the energy of the electro–magnetic field is smaller than a critical value, it will not be able to trigger a transmissible excitation wave traveling as a wave packet. Instead, the energy will just dissipate in the surrounding.
This requirement of “all-or-none” means that ζ should have a fixed cut-off value; it cannot be arbitrarily small. Thus, although the size of the wave packet is not fixed, the total amount of disturbance in the electromagnetic field (as measured by 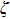
Besides the above considerations, there is another reason for suggesting that ζ2 should be a constant. Recall that ζ2 was defined by Eq. (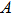
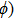
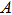
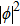
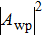

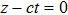
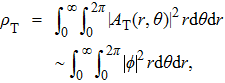 |
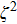
Next, we examine whether our wave packet model is compatible to Planck’s original thinking. In the original work of Planck, his proposal of 
Now, with the findings of this paper, we can explain why Planck’s model could give the correct result. In the black-body radiation, the emitter gives out radiation waves which will be absorbed by the detector. If one accepts that the radiation wave is transmitted in wave packets, our calculation shows that the group energy of each wave packet is proportional to its oscillation frequency, i.e.,
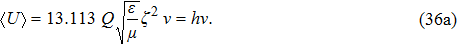 | (36a) |
In Planck’s model, the energy distribution of an emitter is modeled as a linear oscillator. It has a parabolic shape (see Fig. 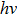

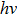

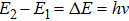
Thus, even though Planck did not calculate the energy content of a radiation wave packet, he could still correctly explain the black-body radiation by using a step-wise energy distribution model. All that he needed to do was to assume that the energy released from the emitters is in packets, which he called “energy quanta”.
Once we can derive Planck’s relation and de Broglie’s relation based on the wave packet model, Heisenberg’s uncertainty principle can be easily explained. If one accepts that a photon is a wave packet of oscillating electro–magnetic field, which follows a Gaussian distribution along the particle trajectory, the half-width of the wave packet in the time domain can be directly determined from the linewidth of the radiation wave. From the condition of Fourier transform, we know 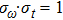

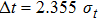



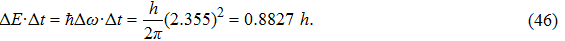 |
This suggests that the product of linewidths in the energy and time domains for a single photon is very close to h. Such a result is consistent with Heisenberg’s conjecture that
 |
Thus, Heisenberg’s uncertainty principle can be interpreted as a direct result of the fact that a photon is a wave packet which follows a Gaussian distribution.
Using this wave packet model, we can also easily obtain the uncertainty principle between 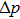
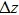

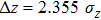
 |
Then, the above relations give
 |
This is consistent with the conjecture of Heisenberg that 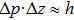
This work represents an approach of using a classical theory to explain the physical basis of h. What we have done so far is to derive Planck’s relation by calculating directly the energy contained within a wave packet based on Maxwell’s theory. Using such an approach, we can also derive the de Broglie relation and Heisenberg’s uncertainty principle. These derivations are straight forward and only based on a simple assumption that the photon is a wave packet of electro–magnetic radiation.
Since Planck’s constant is a fundamental physical constant, it is involved in many areas of study, including the foundation of quantum mechanics,[3,17] quantum field theory,[18,19] the study of chaos,[20] and tunneling,[21] etc. There have been many previous attempts to explain the physical basis of Planck’s constant.[22–26] For example, Galgani and Scott tried to use a classical mechanical model of a 1D particle chain to explain Planck’s relation.[22] They assumed a Lennard–Jones interaction existing between the nearest-neighboring particles and solved the classical equations of motion numerically. For a broad class of initial conditions, Planck-like distributions are obtained for the time averages of the energies of the normal modes. They reported that the action constant entering into such a distribution is of the same order of magnitude as Planck’s constant.[22]
In another study, Ross proposed a possible way of building Planck’s constant into the structure of space-time.[24] This was done by assuming that the torsional defect that intrinsic spin produces in the geometry is a multiple of the Planck length. He showed that by using a simple geometrical assumption, it could lead to the quantization of angular momentum. He thought that such an approach could be considered as a first step to derive the value of 
As an extension of Ross’s study, Duan et al.[26] proposed a new geometrization of Planck’s constant in terms of vierbein theory.[27] They thought that h is also connected with the defects of space-time. A set of invariances including the 
All these previous attempts, however, involve very special assumptions which cannot be directly tested experimentally. Also, they cannot give the explicit value of Planck’s constant, as we did in Eq. (
Recently, quantum communication has become an important new field.[28,29] Obviously, the physical origin of the Planck constant has tremendous importance in this area of research. Since h essentially determines the size of a bit of information in quantum communication, it is very important to know the physical basis of the Planck constant. Thus, this work will be helpful to the further development of this field.
In this work, we show that the energy and momentum of a photon can be determined by treating the photon as a wave packet of electro–magnetic radiation. The following is a summary of the major points of this work:
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |