† Corresponding author. E-mail:
Two-dimensional (2D) materials, such as graphene, phosphorene, and transition metal dichalcogenides (e.g., MoS2 and WS2), have attracted a great deal of attention recently due to their extraordinary structural, mechanical, and physical properties. In particular, 2D materials have shown great potential for thermal management and thermoelectric energy generation. In this article, we review the recent advances in the study of thermal properties of 2D materials. We first review some important aspects in thermal conductivity of graphene and discuss the possibility to enhance the ultra-high thermal conductivity of graphene. Next, we discuss thermal conductivity of MoS2 and the new strategy for thermal management of MoS2 device. Subsequently, we discuss the anisotropic thermal properties of phosphorene. Finally, we review the application of 2D materials in thermal devices, including thermal rectifier and thermal modulator.
Two-dimensional (2D) materials, including graphene, transition metal dichalcogenides (e. g., MoS2 and WS2), black and blue phosphorenes, and h-BN, have attracted extensive attention in recent years. The extraordinary structural, mechanical, and physical properties of 2D materials make this family of materials of great interest in both fundamental science and engineering applications.[1] Due to their excellent mechanical characteristics, these materials are promising for applications in ubiquitous electronics, flexible displays, smart health diagnostics, and wearable computing. For example, single-layer MoS2 is a semiconductor with a large band gap and has been regarded as a promising candidate for field effect transistor applications with high on/off ratio and high mobility.[2–4] By improving sample quality and adopting the appropriate electrode material, the low temperature carrier mobility can be improved significantly.[5] Furthermore, by depositing atop a high-dielectric layer, the carrier scattering due to charged impurity is significantly suppressed, therefore a high room temperature mobility which is close to the theoretically predicted phonon-limited intrinsic value was realized experimentally.[6] With these breakthroughs, 2D materials based integrated circuits (ICs) are highly expected in the near future.
The rapid growth in ICs demands a faster switching speed, larger number of transistors, and higher integration density.[7] With the clock frequency increasing, the power consumption in ICs rapidly climb, which is becoming crucial for ICs because the enhanced local temperature causes degradation in device performance. Furthermore, owing to the atomic thickness of 2D devices, the localized Joule heating in the confined volume of an ultrathin channel can induce more crucial issues in device reliability and performance. The common way for heat transfer is via lattice thermal conduction, which can be governed by Fourier’s law 


Moreover, understanding of the thermal characteristic also directly relates to one important application of 2D materials, i.e., thermoelectric energy conversion and cooling. Usually, a non-dimensionalized figure of merit 

In this article, we would like to give a review on the recent advances in the study of thermal properties of 2D materials, from both the experimental and theoretical points of view. The rest of this article is organized as follows: Section
So far there exist a number of articles and studies on different aspects of thermal and thermoelectric properties of 2D systems. For comprehensive reviews on thermal properties of nanomaterials, please refer to Refs. [10]–[14]. For anomalous heat transport in low-dimensional systems from the viewpoint of fundamental statistical physics, see Refs. [15]–[16]. Due to the limit of length, we mainly address one of the most fundamental issues here, i.e., the fundamental thermal properties of 2D materials.
Graphene and other carbon-based nanomaterials have attracted great research attention due to their high thermal conductivity.[17–19] Various effects on thermal conductivity of graphene have been studied, including size effect,[20–27] substrate effect,[28–33] isotopic doping,[34] surface functionalization,[35–41] strain,[42–45] vacancy,[46–48] and edge configurations.[49–51]
The thermal conductivity of graphene results from a combination of the various effects aforementioned, that is, boundary, mass disorder, structural defect, and interface. These different scattering mechanisms manifest themselves as the dominant ones only in a certain range of frequency regimes. For instance, high frequency phonons are sensitive to mass disorder and vacancy scattering, while low frequency phonons experience little scattering from point defects. On the other side, the contributions from low frequency phonons to thermal conductivity are grossly suppressed by boundary scattering. In a real sample, there exist multiple scattering mechanisms at the same time. For example, for a graphene nanoribbon with mass disorder, there are scatterings from both boundary and point defect, thus the thermal conductivity is determined by the combined effects of these two scattering mechanisms. In graphene nanoribbon, as the high frequency phonon participation ratio is already grossly suppressed by the edge scattering,[34] the isotopic scattering can only induce a much weaker phonon localization effect than that in carbon nanotubes with the same density of isotope. Therefore, although isotopic doping can reduce thermal conductivity of both graphene nanoribbon and carbon nanotube, the reduction behavior is much slower in graphene nanoribbon than that in carbon nanotube: thermal conductivity of graphene nanoribbon is reduced by 12% around the 13C concentration of 5%, while the reduction is 25% in carbon nanotube. Similar to the phononic engineering proposed to control thermal conductivity of quantum well[52] and nanowires,[53,54] this concept is also applicable to manipulate thermal conductivity of 2D materials.
The effects of various scattering factors are summarized in Table
| Table 1.
Summary of different effects on thermal conductivity of graphene. . |
Obviously, almost all of these aforementioned effects reduce the thermal conductivity of graphene. As the high thermal conductivity is one advantage of graphene for thermal management, all the above factors are negative impacts. One important question naturally arises: can we enhance the extremely high thermal conductivity of graphene nanoribbon further?
Using molecular dynamics simulations, Li and Zhang proposed to enhance the ultra-high thermal conduction of graphene nanoribbon by introducing a small gap at the center, i.e., constructing a comb graphene nanoribbon structure.[55]
A typical comb graphene nanoribbon and the corresponding perfect graphene nanoribbon are shown in Fig. 

 | Fig. 1. (color online) Schematic pictures of the whole graphene nanoribbon and comb graphene nanoribbon. Reprinted with permission from Ref. [55], copyright (2013) by the Frontiers of Physics. |
 | Fig. 2. The average heat flux enhancement ratio versus graphene nanoribbon width. The temperature is 300 K. Reprinted with permission from Ref. [55], copyright (2013) by the Frontiers of Physics. |
More interesting, this enhancement ratio depends on graphene nanoribbon width remarkably. The enhancement ratio reaches maximum when width W = 6.3 nm. For the comb graphene nanoribbon, with width increasing, more phonons are excited in each branch, and the strong phonon–phonon scattering leads to a weakening of the enhancement ratio. On the other side, with width decreasing, the impact of edge scattering increases, which decreases the enhancement ratio. Thus there is an optimal width to maximize this enhancement effect. For a graphene nanoribbon with width of 6.3 nm, a 0.48 nm wide gap can enhance its average heat flux of 23%.
Unlike the ultra-high thermal conduction in graphene, thermal conductivity of monolayer MoS2 is much lower. Using molecular dynamics simulations, Liu et al. explored thermal conductivity of monolayer MoS2 sheet and nanoribbon.[56] In addition to the low thermal conductivity, the length dependence is also quite different from that of carbon based nanomaterials.[57,58] In graphene, its thermal conductivity increases with length increasing, even the length is more than 700 nm.[26] However, as shown in Fig.
 | Fig. 3. (a) Thermal conductivity of MoS2 nanoribbons as a function of length. (b) The data from panel (a) plotted as 1/k versus 1/L. Reprinted with permission from Ref. [56], copyright (2013) by the American Institute of Physics. |
From the kinetic theory of phonon transport and in consideration of the phonon–phonon scattering and the phonon–boundary scattering, it was found that the inverse of thermal conductivity versus the inverse of the nanoribbon length should be linear, and the phonon mean free path can be obtained from the intercept and slope of the linear relationship. For monolayer MoS2, the estimated phonon mean free path according to phonon–phonon Umklapp scattering is extracted to be only 5.2 nm,[56] about two orders of magnitude lower than that of graphene, which is believed to be responsible to the low thermal conductivity of monolayer MoS2 sheet.
Using first-principles calculations within the framework of density functional perturbation theory, Cai et al. investigated the anharmonic characteristic of phonons in monolayer MoS2 sheet.[59] In contrast to the negative Grüneissen parameter occurring in low-frequency modes in graphene, a positive Grüneissen parameter was found in the whole Brillouin zone in monolayer MoS2, which demonstrates that monolayer MoS2 sheet possesses a positive coefficient of thermal expansion. Combined with the nonequilibrium Green’s function calculations, the room temperature thermal conductivity of monolayer MoS2 is around 23.2 W/(mK), two orders of magnitude lower than that of graphene. This is consistent with the experimental reports[60,61] and theoretical results based on other computational methods.[62–65] It is worth mentioning that in Ref. [63], Li et al. studied thermal conductivity of MoS2 using the Boltzmann transport equation method. It was found that thermal conductivity increases with sample size up to 
It was predicted that nanostructured materials will have improved thermoelectric performance compared to the bulk counterparts, due to the quantum confinement in the electron band structure. The high power factor and low thermal conductivity in silicon nanowires have demonstrated that 1D thermoelectric devices[68] can be realized in semiconductor nanowires. However, the ultra-high thermal conductivity of graphene[10] offsets its advantages in power factor and limits its application as efficient 2D thermoelectric materials. The low thermal conductivity (around tens of W/mK) of monolayer MoS2 raises the exciting prospect that it can be used for high-performance thermoelectric application.
Due to the increased number of interfaces, contact thermal resistance plays an important role in the thermal transport in nanoscale. For MoS2 based device, the source and drain contacts are usually made of metals. Using molecular dynamics simulations, Liu et al. studied interfacial thermal conductance between MoS2 sheet and Au.[69] In general, there are two types of interface geometries between metal surfaces and 2D MoS2 sheets: side contact and edge contact. In the side contact configuration, the metal surface interacts with the basal plane of MoS2 via van der Waals interactions, which leads to large contact electrical resistance. On the other hand, for the edge contact configuration, the interface between monolayer MoS2 and Au electrode can be formed through chemical interaction,[70] suggesting high thermal transport in this contact. The binding energies between MoS2 and Au surfaces with various orientation angle θ are shown in Fig. 




 | Fig. 4. (color online) (a) MoS2 on a (001) Au surface with a rotation angle of 0°. (b) MoS2 on a (110) Au surface with a rotation angle of 90°. (c) MoS2 on a (111) Au surface with a rotation angle of 30°. Mo and S atoms are shown in purple and yellow respectively, and Au atoms are shown in cyan, brown, and red for the first, second, and third layers, respectively. (d) Binding energy of MoS2 on different crystal Au surfaces. Reprinted with permission from Ref. [69], copyright (2016) by the Springer. |
The interfacial thermal conductance values are shown in Fig. 
 | Fig. 5. (color online) Dependence of interfacial thermal conductance (ITC) on Au crystal surfaces and contact directions. Reprinted with permission from Ref. [69], copyright (2016) by the Springer. |
It is reported that S vacancy can reduce the thermal conductivity of monolayer MoS2 significantly, with a 0.25% S vacancy concentration leading to a 20% reduction in the thermal conductivity with respect to that of pristine MoS2.[72] However, S vacancies introduced in the central region of MoS2 have a negligible effect on the interfacial thermal conductance. This can be understood from the atomic vibrational spectrum. For the pristine MoS2, a notable peak of 13 THz exists in its vibrational spectrum. However, for the Au atoms, the cut-off frequency is around 5 THz. It is the mismatch in phonon density of states that hinders heat transport across the interface and leads to interfacial thermal resistance. In defective MoS2, the missing atoms lead to significant changes in phonon density of states in the high frequency region. However, the missing atoms have almost no influence on phonon density of states in the low frequency region (
Unlike the single MoS2 transistor device, for future MoS2 based ICs, due to the larger number of transistors or higher functional density, heat dissipation will become a crucial issue. The first way for heat transfer is lattice thermal conduction, which is described by Fourier’s law 

In addition to lattice thermal conduction, heat energy also can be transferred by radiation. In recent years, near field radiation has attracted extensive research interest, which can break the limit due to blackbody law.[73] Based on the idea of near field radiation, Peng et al. designed a new methodology for thermal management of MoS2.[74] The considered configuration is shown in Fig. 

 | (1) |

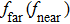
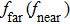
 | (2) |
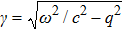
 | Fig. 6. (color online) Schematic of simulation model. Reprinted with permission from Ref. [74], copyright (2015) by the American Institute of Physics. |
Due to the large band gap in MoS2, the inter-band transition processes of MoS2 are the dominant channels. The inter-band transition peaks can be adjusted by the Fermi energy of MoS2: when the Fermi energy of MoS2 is close to its conduction band edge, it leads to a sharp resonant peak. This low frequency resonant peak provides the main channel for near field radiation heat transfer. For the resonant case, three orders of heat enhancements in near field radiation comparing with the blackbody limit is realized, and this ratio increases quickly with the vacuum gap decreasing. However, the near field radiation heat transfer is very sensitive to the chemical potential and Fermi energy of graphene and MoS2. With slight deviation from the ideal resonant state, the heat transfer decreases significantly.
It is necessary to compare the cooling process by near field radiation and that through the in-plane lattice thermal transport. The schematic of a MoS2 device with near field radiation cooler is shown in Fig. 




 | Fig. 7. (color online) (a) Temperature distribution of near field radiation heat transfer (NFRHT) based cooling device. (b) Ratio of NFRHT and in-plane heat conduction. (c) Energy power of NFRHT and in-plane heat conduction as a function of length. (d) Ratio of NFRHT and in-plane heat conduction as a function of length. Reprinted with permission from Ref. [74], copyright (2015) by the American Institute of Physics. |
Due to its unusual structure and electronic properties, phosphorene has drawn considerable attention.[76,77] For example, layer-dependent electronic properties[78,79] and edge dependent electronic properties[80–82] have been explored. A strong anisotropy was found in the carrier mobility of phosphorene,[83,84] and its carrier mobility can be increased by covering high-k materials.[83] The interesting feature was predicted theoretically for phosphorene in Li-battery applications[85] and observed experimentally.[86]
The thermal properties of phosphorene are also interesting, and not observed in other 2D materials such as graphene or MoS2. Using first-principles calculations and the nonequilibrium Green’s function method, Ong et al. explored the ballistic thermal conductance of monolayer phosphorene.[87] As shown in Fig. 
 | Fig. 8. (color online) The thermal conductance in the zigzag and armchair directions as a function of temperature (a) at different biaxial strains, (b) at uniaxial strain applied in the zigzag direction, and (c) at uniaxial strain applied in the armchair direction. (d) The thermal conductance anisotropy at different strain values for uniaxial strain. Reprinted with permission from Ref. [87], copyright (2014) by the American Chemical Society. |
The thermoelectric properties of phosphorene have also been investigated.[94–97] Although a high thermoelectric figure of merit ZT is expected, unfortunately, a theoretical value for ZT is found to be 0.14 in p-type impurity-free phosphorene at 500 K, with considering both optical phonons contributions and the high anisotropy which provides extra phase space for electron–phonon scattering, based on density functional perturbation theory and Wannier interpolation.[96] By analysing the various effects on ZT, Zhou et al. proposed possible routines to enhance figure of merit ZT.[97] In the weakly doped condition, the Seebeck coefficient of monolayer phosphorene is high. Thus the electrical/thermal conductance ratio is the major factor that affects its thermoelectric performance, due to the low electron conduction and high thermal conduction. In this regime, the phonon thermal conductance plays a major role in comparison with electronic thermal conductance. Therefore, the reduction of lattice thermal conductivity will significantly enhance the ZT, such as the creation of a superlattice to localize the long-wavelength phonons and introducing mass-disorders and/or edge roughness to suppress the phonon transmissions. On the other side, in the highly doped condition, the reduction of the Seebeck coefficient and the rapid increase of electronic thermal conduction are the major factors that limit ZT. In this regime, controlling the electronic structure is critical for boosting ZT. Possible methods include electromagnetic field modulation and/or strain engineering.
Fabrication of the phononic crystal structure has been intensively studied to reduce thermal conductivity with weak influence on electrons.[98] Therefore, if a similar trend holds for phosphorene, the phosphorene phononic crystal would have much higher ZT with respect with the pristine phosphorene monolayer in a weakly doping regime, as discussed above.
Using molecular dynamics simulation, Xu and Zhang[99] studied the thermal properties of the phosphorene phononic crystal, which is a nanomesh structure with periodically arranged pores, by arranging a rectangular pore into each rectangular supercell of phosphorene. The dimensions of each pore and each supercell are 














 | Fig. 9. (color online) The room-temperature thermal conductivity of phoshphoren phononic crystal versus the size of pores. For more details, please refer to Ref. [99]. Reprinted with permission from Ref. [99], copyright (2016) by the Institute of Physics. |
In nanostructures, phonons usually experience intensive phonon–boundary scattering. There are two types of phonon–boundary scattering processes: particle-like incoherent scattering and the wave-like coherent scattering. The latter will lead to Brillouin zone folding and new phonon dispersion due to wave interference. To realize the coherent scattering, the periodicity of the phononic crystal must be comparable or smaller than the phonon mean free path. The phonon mean free paths of phosphorene at the two directions are 141.4 nm (zigzag direction) and 43.4 nm (armchair direction),[88] which must be larger than the periodic length considered here. Thus the coherent picture is a reasonable approximation to describe the frequent phonon scattering at the high-density pore boundaries. In this condition, the pore boundary can be treated as an intrinsic part of the unit cell of the phosphorene phononic crystal, rather than an extrinsic scattering source.
In Fig. 
 | Fig. 10. (color online) A comparison of phonon dispersions and phonon lifetimes between in the pristine phosphorene and in the phononic crystal. Reprinted with permission from Ref. [99], copyright (2016) by the Institute of Physics. |
Regarding the phonon lifetime, since the zone folding in the phononic crystal has shifted the phonon dispersion, the selection rules for phonon–phonon scattering will vary. As a result, the phonon lifetime should also be influenced. As is shown in Fig.
Recently, phononics (thermal) devices have attracted extensive interest for the understanding of how heat energy is transported, distributed, and converted from fundamental science to applied research field.[100] One of the motivations is to realize on- and off-state by controlling the thermal conduction, and furthermore to realize thermal circuits by using these novel phononics devices. In addition to the application in information processing, the thermal devices also have broad applications for thermal management in the future.
So far, all the thermal rectification phenomena are observed in hetero-structures. In these junctions, phonon vibrational spectrums at two sides of the junctions are different. Moreover, the mismatch depends on temperature. The ideal case is that under positive temperature bias, the overlap of phonon spectrum of the two ends increases. However, with negative temperature bias, the mismatch enlarges. Therefore, the total thermal current under positive temperature bias is larger than that under the negative bias, which is similar to the characteristic of an electrical diode.
Due to its ultra-high thermal conductivity, graphene is an ideal candidate to realize this function. The thermal rectification effect was observed in graphene nanoribbons with trapezia shape,[101,102] a junction constructed by two rectangular graphene nanoribbons with different widths,[102] Y-shaped graphene,[103] graphene with inhomogeneous mass distribution,[104] reduced graphene oxide with asymmetric shape,[105] and graphene composite with binary solid–liquid phase change materials.[106] Related theoretical and experimental works are summarized in Table
| Table 2.
Summary of different thermal rectifier based on graphene. . |
In addition to the rectifier, the electronic modulator is also an important electrical element and has been widely used. However, its thermal counterpart, the thermal modulator, has not been well studied. In 2015, a new concept of thermal modulator was predicted theoretically by Liu et al.[107]
The graphene-based thermal modulator is shown in Fig.
 | Fig. 11. (color online) Schematic of graphene-based thermal modulator. Reprinted with permission from Ref. [107], copyright (2015) by the Springer. |
 | Fig. 12. (color online) (a) Heat flux along the graphene thermal modulator as the function of clamp–graphene gap G. (b) Heat flux along the graphene thermal modulator as the function of the external pressure P. Reprinted with permission from Ref. [107], copyright (2015) by the Springer. |
The underlying mechanism for the thermal modulation was also explored. In the free-standing single-graphene, there are six phonon polarization branches: in-plane transverse acoustic (TA) and optical (TO), in-plane longitudinal acoustic (LA) and optical (LO), and out-of-plane acoustic (ZA) and optical phonons (ZO). However, for graphene sandwiched between two clamps, the van der Waals interaction between clamp and graphene induces significant change in the out-of-plane phonon modes with flattening and shifting characteristics. The shift in ZA modes leads to a mismatch in phonon dispersion at the interface, which leads to the nontrivial reduction in heat flux. As the clamp–graphene gap decreases, the shift in ZA mode increases, which results in the increase of the interface-phonon scattering and a further reduction of heat flux. Thus the heat flux through the system can be controlled by the graphene-clamp gap. More interesting, the performance of this thermal modulator can be improved by increasing the number of clamps or interfaces. For example, splitting a 10-nm-clamp into two clamps in series, each with 5 nm long, can increase the change range of heat flux: at a pressure of 50 GPa, the maximum reduction in heat flux increases from 27% (single-clamp) to 40% (double-clamp). Hence, in constructing the proposed thermal modulator experimentally, a linear arrangement of clamps in series can be highly effective in increasing the modulation capability.[107]
This article presents an overview of the thermal properties of 2D materials. Our intent is to present a state-of-the-art view in this fascinating field, with a balanced experimental and theoretical perspective. It is hoped that the insights and understandings revealed and summarized here provide an important reference and guideline for the applications of 2D materials in thermal management and heat-to-electricity conversion. Due to the limit of length, we mainly address the fundamental thermal properties of the 2D material family. So far there exist other review articles on different aspects of thermal and thermoelectric properties of graphene, MoS2, and phosphorene.[108–113]
In addition to graphene, MoS2, and phosphorene, very recently more 2D materials have been discovered, such as h-BN, silicene, and stanene.[114–126] The thermal and thermoelectric properties of these new 2D materials also deserve systematic investigations. Moreover, in nano systems, the increased number of interfaces plays a more and more important role in heat conduction. Although interfacial thermal resistance of some hybrid nanostructures have been explored,[127–135] considering the complexity and variety of new 2D materials and their hybrid nanostructures, more systematic studies are needed to further understand the fascinating properties of this class of materials and to seek their novel applications in thermal management and heat-to-electricity conversion.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] |


