† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11222544), the Fok Ying Tung Education Foundation (Grant No. 131008), the Program for New Century Excellent Talents in University, China (Grant No. NCET-12-0121), and the National Key Basic Research Program of China (Grant No. 2011CB922004).
Based on a first-principles approach, we establish an alternating-current (AC) relaxation theory for a rotating metallic particle with complex dielectric constant 
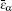
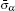
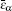
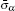
The structures of various systems, such as colloidal suspensions including electrorheological fluids,[1–3] magnetorheological suspensions,[4–7] ferrofluids,[8–11] living cells suspensions,[12] and so on, are very sensitive to the change of interparticle forces. Unfortunately, some shearing flow that is inevitable in experiments and natural environments can cause the rotation of the colloidal particles,[13–23] thus reducing the interparticle force to some extent. An interaction between a rotating electric field and suspended particles or cells can also lead to a rotational motion of the particles. This phenomenon, known as electrorotation, has been increasingly employed as a sensitive tool for noninvasive studies of a broad variety of microparticles, ranging from living cells to nanowires, seeds as well as synthetic materials.[24–29] In addition, insulating particles suspended in a liquid with low conductivity can also rotate in the presence of an electric field, which leads to the so-called negative effective viscosity effect.[30,31]
The dielectric relaxation can affect the inter-particle force, and even the property of the semi-conducting materials.[32–34] So far, the relaxation of polarized charges in dielectric particles has been investigated within the well-known Maxwell–Wagner relaxation theory. However, it was shown that the Maxwell–Wagner relaxation time is valid for an isolated stationary dielectric sphere or infinite large plank, whose dielectric responses are represented by a dielectric constant and electric responses by a conductivity.[35]
When a dielectric particle starts to rotate, the polarization charges tend to deviate from the original position due to the rotation of the dielectric particle. On the other hand, the charges tend to return to the original position due to the directed external field. Thus, at dynamic equilibrium, the two competitive effects can change the polarization charge distribution. As a result, this change affects the interaction between the two particles one of which is rotating. The same process also happens when a metallic particle substitutes for the dielectric one. However, for the extremely high conductivity of the metallic material, it is believed that free charges on the surface of the metallic particle will not cause an obvious force decrease in a low rotation speed. On the contrary, Tao and Lan[36] experimentally reported that the rotation of a metallic particle can reduce significantly the attracting interparticle force between the rotating metallic particle and a stationary dielectric or metallic one in argon gas. To the best of our knowledge, this was the first direct experiment conducted on the interparticle force between two touching rotating particles. Tan et al.[37] found that the local electric field between two metallic particles weakens as one rotates faster, which can be used to qualitatively explain the phenomenon of Tao and Lan’s work.[36] However, a quantitative explanation is still lacking for explaining Tao and Lan’s observations,[36] which is important for practice. To solve this, we believe that the relaxation processes in dynamic metallic particles should be understood carefully, which are also expected to receive a broad interest in various fields related to dynamics in (soft) condensed matter. Reference [38] described a method to solve similar systems. However, only dielectric particles were under their consideration. In this work, we improve the method in Ref. [38]. Based on a first-principles approach, we establish a relaxation theory for dynamic metallic particles in the presence of an external AC field, thus being called AC relaxation theory.
This paper is organized as follows. In Section 2, we establish an AC relaxation theory for dynamic metallic particles on the basis of a first-principles approach. In Section 3, the comparison between theory and experiment is presented, which is followed by a conclusion in Section 4.
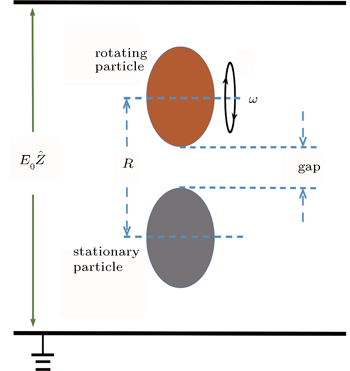
Let us consider two spherical particles in an external electric field 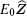
The value of ω can be controlled artificially (e.g., the rotating particle may be connected to a motor[36]). In spherical coordinates, the electric potential Φ satisfies the Laplace equation and the general expressions for Φh(
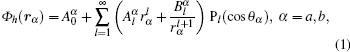
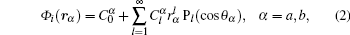
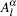
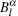
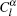
Applying the boundary conditions, i.e., the continuity of the potential and the electric displacement on the surface of particles, we obtain two sets of relations between the unknown coefficients:
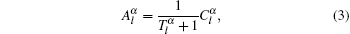
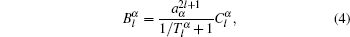

Here εα and εh are the dielectric constants of particle α and the host, respectively, and aα is the radius of particle α.
Since we try to introduce the effect of free charges which may exist on the surface of metallic particles, the conductivity of the particle should be considered. In that case, the complex dielectric constant εα can be written as
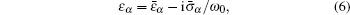
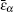
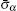
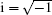
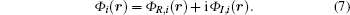
The polarized and free charge distributions σst on the surface of the metallic particle are related to the discontinuity in the electric field across the surface through

In the calculation below, we deal with the complex parameters directly.
The remaining unknown coefficients 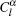
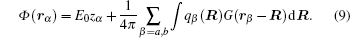
Here
Comparing Eqs. (
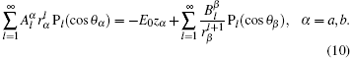
In the experiment of Ref. [36], the two particles were arranged along the
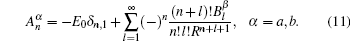
Thus, all the coefficients 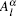

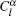
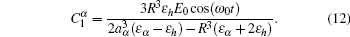
Here ω0 is the frequency of the applied field. For particles with different dielectric constant and radius, the coefficients 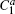
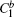

The parameters are complex forms as described by Eq. (
Once the rotation appears, the displaced original polarized and free charge distributions deviate from the static distribution. The distribution will tend to relax to an equilibrium distribution at a certain rate 1/τ where τ means the relaxation time, which is dependent on the material forming the particles, the geometry of the particles, and some other elements like rotation speed and circumstance. Here, according to Eq. (

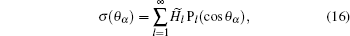
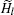
The force exerted on a particle can be found by evaluating the derivative of the energy with respect to particle displacement in space. The change in electrostatic energy due to the introduction of particles into the host medium in the presence of an electric field

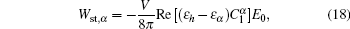
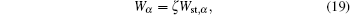
Now, by taking the derivative of the energy, a formula relating the angular velocity ω of the rotating particle to the induced force
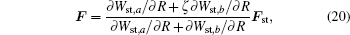
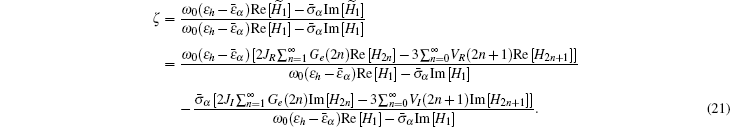
Here, we only keep the first three terms in our numerical calculation for each relaxation time, and the contributions from all the other terms are small enough to be neglected. The coefficients VR, VI, JR, JI, and Ge are respectively given by

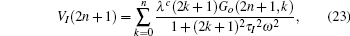
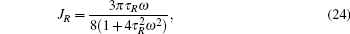
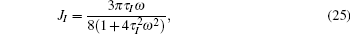
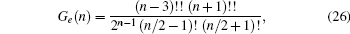
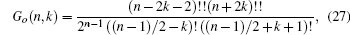

In Eqs. (
In the experiment,[36] two spherical particles of diameter 19.06 mm were arranged vertically inside a capacitor composed of two horizontal electrodes. One of the particles, which could move up and down to adjust the gap between particles, was connected to a motor and was able to rotate around the horizontal axis. Another one rested on a microbalance. The whole device was placed inside a glove box, which was filled with dry argon gas. When there was no electric field, the reading on the microbalance was just the weight of the stationary particle. When an electric field was applied, the induced attracting force between the rotating metallic particle (cooper) and the stationary metallic particle (cooper) or the dielectric one (polyamide) reduced the reading on the microbalance. Thus, the attracting force between the two particles was able to be determined.
Now we are in a position to compare theory and experiment. For this purpose, consistent with the experiment,[36] the diameters of particles are also set to be 19.06 mm. The distance between the centers of the two particles, R, which is used in our calculations, can be got by R = gap + 19.06 mm, where the gap is the surface-to-surface separation between the particles (see Fig.
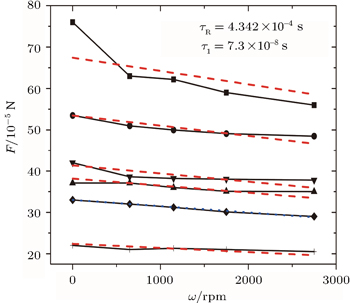 | Fig. 2. Fitting of the experimental data of a rotating metallic particle (copper) and a stationary metallic one (copper) in an AC electric field with frequency ω0 = 300 Hz. The symbols denote the experimental data which are extracted from Ref. [36]. From upper to bottom: R = 19.314 mm (or gap = 0.254 mm) and E0 = 100 V/mm; R = 19.441 mm (or gap = 0.381 mm) and E0 = 100 V/mm; R = 19.314 mm (or gap = 0.254 mm) and E0 = 80 V/mm; R = 19.568 mm (or gap = 0.508 mm) and E0 = 100 V/mm; R = 19.441 mm (or gap = 0.381 mm) and E0 = 80 V/mm; R = 19.568 mm (or gap = 0.508 mm) and E0 = 80 V/mm. Similarly, according to our theory [Eq. ( |
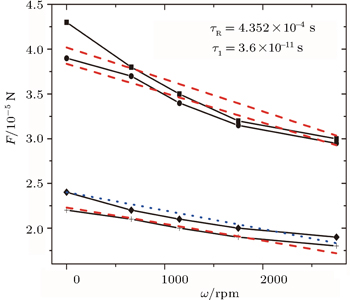 | Fig. 3. Fitting of the experimental data of a rotating metallic particle (copper) and a stationary dielectric one (polyamide) in an AC electric field with frequency ω0 = 300 Hz. The symbols denote the experimental data which are extracted from Ref. [36]. From upper to bottom: R = 19.314 mm (or gap = 0.254 mm) and E0 = 100 V/mm; R = 19.441 mm (or gap = 0.381 mm) and E0 = 100 V/mm; R = 19.441 mm (or gap = 0.381 mm) and E0 = 80 V/mm; R = 19.568 mm (or gap = 0.508 mm) and E0 = 80 V/mm. According to our theory [Eq. ( |
For the rotating metallic sphere, the well-known Maxwell–Wagner relaxation time[35,42] predicts 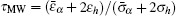
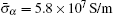
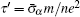
According to our results, the relaxation time τR is generally much longer than τI. In fact, the τR sources from polarized charges (described by 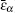
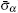
When displaying the theoretical results in Figs.
| Table 1. Relaxation times, τR and τI, for obtaining good fitting with experimental data of Fig. |
| Table 2. Relaxation times, τR and τI, for obtaining good fitting with experimental data of Fig. |
Here some comments are in order. Our method introduced the conductivity (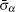
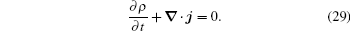
Here, the current can be written as Ohm’s law 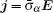
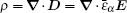
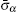
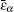
To sum up, based on a first-principles approach, we have established an AC relaxation theory for dynamic metallic particles. An imaginary part has been introduced to the method established in Ref. [38] because the particle is conducting. The relaxation times were obtained according to the fitting with the experimental data. Good agreement between theory and experiment has shown that the relaxation processes of surface-polarized and free charges yield the reduction in the attracting interparticle forces between a rotating metallic particle and a stationary metallic or dielectric one. Our theory can help to determine the relaxation time of dynamic metallic particles in many fields.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 |