† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11574188) and the Project for Excellent Research Team of the National Natural Science Foundation of China (Grant No. 61121064).
A kind of photonic crystal structure with modulation of the refractive index is investigated both experimentally and theoretically for exploiting electromagnetically induced transparency (EIT). The combination of EIT with periodically modulated refractive index medium gives rise to high efficiency reflection as well as forbidden transmission in a three-level atomic system coupled by standing wave. We show an accurate theoretical simulation via transfer-matrix theory, automatically accounting for multilayer reflections, thus fully demonstrate the existence of photonic crystal structure in atomic vapor.
Electromagnetically induced transparency[1,2] (EIT) is a fascinating quantum coherence phenomenon to suppress resonant absorption[3] and slow light pulse,[4] manipulate atomic entanglement,[5] and realize high efficiency quantum memory.[6,7] It has been successfully integrated on a semiconductor chips,[8] promoting the development of quantum optical device. Recently, EIT shows the wide applications in the field of cavity optomechanics,[9] optical lattice for cold atoms,[10] and hybrid atom-molecular system.[11,12] Photonic crystal structure[13–16] with periodically varying refractive index is capable of controlling the flow of light wave. The main feature is to open photonic band gaps (PBGs) resulting from Bragg scattering.
The combination of EIT and photonic crystal is an attractive research for quantum communication network. EIT-based photonic crystal structure can be constructed in a three-level atomic system driven by a standing wave, which results in spatially modulated absorption and refractive index.[17] This photonic crystal structure generates a reflected field, which is explained as either electromagnetically induced grating (EIG)[18–20] or four-wave mixing (FWM) process.[21,22] At the same time of reflection, electromagnetically induced absorption (EIA)[23] happened to the probe field in thermal vapor. Therefore, much attention has been paid to the applications in all-optical routing,[24] optical controllable Bragg mirror,[25] and optical diode.[26] Bae et al. and Andy et al. observed reflection signals with efficiencies of 11.5%[20] and 7%,[24] respectively, accompanying a decrease in transmittance of the probe field[19,20,24] due to EIG reflections and spatial interference effects from the modulated absorption in rubidium atoms. For the application in high performance quantum optical device, we should improve the reflection efficiency to a higher level as well as achieve strong absorption. Here, we experimentally obtain 35% reflection and simultaneously achieve the complete opaque to the probe field in a spatially modulated photonic crystal grating with cesium vapor.
In these previous studies, diffraction/reflection signals were obtained by solving the wave equation of the probe field with the consideration of spatial modulation of coupling field.[18] On the other side, the explanation of FWM[21,22] focused on the nonlinear susceptibility exploiting perturbation theory without regard to the spatial modulation. In the present paper, by combing the periodic modulation and EIT, we show good agreement between numerical simulation and experimental observation with using the transfer-matrix theory,[27,28] which is proved to be the most effective method to study the light propagation in periodically modulated dielectric. The consistence fully demonstrates the existence of periodic modulation thereby helpfully understanding the physics behind multilayer reflections in photonic crystal structure.
We perform the experiment in a three-level system with one excited level |a〉 (62P1/2,F′ = 4), and two ground levels |b〉 (62S1/2,F = 4) and |c〉 (62S1/2,F = 3) of the 133Cs D1 line, see Fig.
 | Fig. 1. (a) Λ-type three-level system driven by standing wave (SW) coupling field. (b) Experimental setup. PBS: polarizing beam splitters, PD: photo detector. |
If the backward coupling field is blocked, this atom-field interaction exhibits typical EIT as shown in Fig.
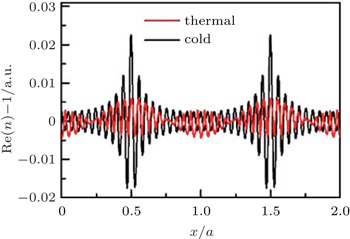
SW coupling field varies the absorption of probe field along the x direction with a periodicity of a = λc/2. Then, the periodical modulation of absorption gives rise to a similar modulation of refractive index limited by Kramers-Kronig relations[29] as shown in Fig.
Considering the optical transition of |a〉 ↔ |b〉 driven by the weak probe field, off-diagonal density matrix element ρab is represented as a Fourier series in this periodical modulated dielectric
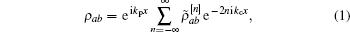
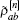
For an atom moving with velocity v along the x direction, the frequencies of the probe, forward and backward coupling fields are Doppler shifted by kpv, kcv, and −kcv, respectively. Consequently, the two counter-propagating coupling fields have a frequency difference 2kcv. The optical responses for all atoms with Maxwell velocity distribution 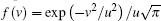
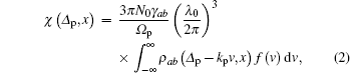

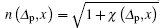
It can have a good accuracy to sum the spatial harmonics from n = −20 to 20 in Eq. (
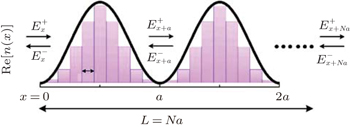
Transfer matrix relates forward- and backward-going waves on both sides of an arbitrary optical element.[27] In order to describe the probe propagation through multilayer dielectric, the field amplitude at arbitrary position x is divided into both forward- and backward-going parts as shown in Fig.
As shown in Fig.
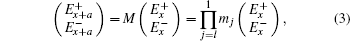

The grating period is a = λc/2 ≈ 447 nm, therefore, 75-mm-long atomic vapor can be regarded as the stack of an abundance of but finite periods in experiment, whose length is L = Na (N ≫ 1 is the number of periods). The probe amplitude at the exit of the cell is expressed by
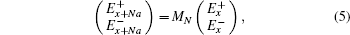
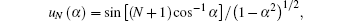
In addition, transfer matrix MN holds the expression of
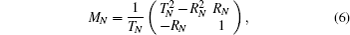
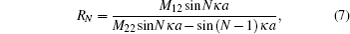
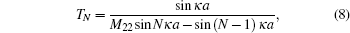
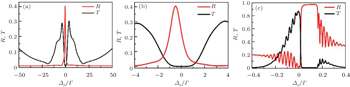
Figure
In this work, we experimentally investigate a kind of photonic crystal structure in three-level cesium vapor driven by standing wave coupling field. A similar effect of frequency stop band, on-resonance high-efficiency Bragg reflection signal and forbidden transmission are obtained. Transfer-matrix method is used to give a very good numerical simulation with taking into account the characteristic of periodic refractive index modulation. It is proved that photonic crystal structure really exists in this coupled atom-field system due to the consistence between experimental and theoretical results. Furthermore, perfect PBG is predicted in ultracold atoms, providing potential applications in optical communication network and promise to be integrated on chip.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 |