Atomic coherence and quantum interference are the basic mechanism for controlling the optical properties of the medium. The discovery of electromagnetically induced transparency (EIT)^[1,2] has led to many interesting phenomena such as lasing without population inversion,^[3] enhanced Kerr nonlinearity,^[4] electron localization,^[5,6] optical bistability (OB),^[7–25] and other interesting phenomena.^[26–33] Among these, optical bistability has been developed due to its potential application in all optical switching and optical transistors which are necessary for quantum computing and quantum communications. The bistable threshold intensity and hysteresis loop can be controlled by several and different methods such as field-induced transparency,^[7] quantum interference,^[8–11] phase fluctuation,^[12–14] squeezed state field,^[15–17] etc.^[18–25]

It should be pointed that similar phenomena based on atomic coherence and quantum interference in semiconductor quantum wells and quantum dots have also been analyzed due to their important applications in opto–electronic and solid-state quantum information science.^[34–40] There are many proposals for controlling the OB and OM in semiconductor quantum wells and quantum dots.^[41–45] For example, Wang and Yu^[41] investigated the OB behavior in an asymmetric three-coupled quantum well structure inside a unidirectional ring cavity. They found that by controlling the assisting coherent driven field and the frequency detuning of the two control laser fields the appearance and disappearance of OB can be easily controlled. In another study by Wang and Yu,^[42] OB and OM behaviors in polaronic materials doped with nanoparticles inside an optical ring cavity have been discussed. Li^[43] studied the behavior of OB in a semiconductor quantum well system with tunneling-induced interference. In our recent study, we studied the behaviors of OB and OM by biexciton coherence in a multiple quantum well nanostructure.^[45]

More recently, due to unique selection rules of graphene which results from its magneto-optical properties and the peculiar thin graphite layers some researchers are interested to investigate the optical properties of graphene.^[46–49] Graphene has unusual electronic and optical properties stemming from linear, massless dispersion of electrons near the Dirac point and the chiral character of electron states.^[50–52] Magneto–optical properties of graphene and thin graphite layers are particularly peculiar, showing multiple absorption peaks and unique selection rules for transitions between Landau levels.^[46,47] The strong optical nonlinearity of graphene, like most of its unique electrical and optical properties, stems from the linear energy dispersion of carriers near the K, K′ points of the Brillouin zone. As a result, the electron velocity induced by an incident electromagnetic wave is a nonlinear function of induced electron momentum. The nonlinear electromagnetic response of classical charges with linear energy dispersion has been studied theoretically.^[53–55] Moreover, graphene has the outstanding optical properties,^[56,57] such as strong light-graphene interaction, broadband and high-speed operation. It seems to be a good candidate for designing tunable optical device that operates in both THz and optical frequency ranges due to the tenability of the charge carrier density and conductivity by the bias voltage of graphene. In strong magnetic field regime the generation of polarized-entangle photon and nonlinear frequency conversion of THz surface plasmons based on the nonlinear optical interaction have been analyzed.^[58–61] In addition, it has been demonstrated that the bilayer graphene can exhibit a giant and tunable second-order optical nonlinearity and may have potential applications in new compact photonic and optoelectronic devices.^[62] Graphene in a magnetic field can be compared with coupled quantum well heterostructures, where one can also achieve a fully resonant nonlinear optical interaction involving a cascade of allowed intersubband transitions.^[58,59] The formation and ultraslow propagation of infrared spatial solitons originating from the balance between nonlinear effects and the dispersion properties of the graphene under infrared excitation have been discussed.^[63] The matched infrared soliton pairs based on four-wave mixing (FWM) in Landau-quantized graphene by using the density-matrix method and perturbation theory have been discussed by Ding et al.^[64] It is found that the matched spatial soliton pairs can propagate through a two-dimensional crystal of graphene and their carrier frequencies are adjustable within the infrared frequency regime. In our recent study, we showed the possibility of controlling the group index switching in graphene under the action of strong magnetic and infrared laser fields,^[65] and discussed the absorption, dispersion, and group velocity of light via incoherent pumping field in a four-level Landau-quantized graphene nanostructure.^[66] To the best of our knowledge, the controls of optical bistability and multistability in Landau-quantized graphene nanostructure with double dark resonances have not yet been reported. In the present work, we study the OB and OM properties in a unidirectional ring cavity doped by four-level Landau-quantized graphene nanostructure. Our proposed model is mainly based on Ref. [63], however, our work is drastically different from that. First and foremost is that we are interested in showing the controllability of the optical bistability and multistability behaviors. Second, the properties of OB and OM can be controlled in double dark resonances conditions. Third, a very important advantage of our investigation can be used for the optimal design of graphene system to achieve low-threshold all-optical bistable and multistable systems.

In the presence of a strong magnetic field a doped graphene system with four level energy levels that form a ladder-type configuration is shown in Fig. 1. According to the peculiar selection rules of graphene, i.e., Δ|n| = ±1 (n is the energy quantum number) as opposed to Δn = ±1 for electrons, the chosen transitions between Landau levels are dipole allowed. Such a system has been already used for studying the giant optical nonlinearity, nonlinear frequency conversion, generation of entangled photons, and formation of ultraslow solitons.^{[58,59,61–64]} For a magnetic field in the range of 0.01 T–10 T, the optical transitions between the adjacent Landau levels (LLs) in graphene fall into the infrared-to-THz region. The electric field vector of the system can be represented by with e_j and k_j (j = 1,2) being the unit vectors of polarization direction and wave vector, respectively.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) LLs near the K point superimposed on the electronic energy dispersion without a magnetic field E = ±vF |p|. The magnetic field condenses the original states in the Dirac cone into discrete energies. The LLs in graphene are unequally spaced: (b) Energy level diagram and optical transitions in graphene interacting with two continuous-wave control fields, a cycling coupling field, and a weak pulsed probe field. The states |1〉, |2〉, |3〉, and |4〉 correspond to the LLs with energy quantum numbers n = −2,−1, 0, and 1, respectively. Graphene monolayer is a one-atom-thick monolayer of carbon atoms arranged in a hexagonal lattice, which we will treat as a perfect two-dimensional (2D) crystal structure in the x–y plane.

The optical excitation via a linearly polarized continuous-wave (CW) laser control field induces the intra-LL transitions |2〉 ↔ |3〉 and |3〉 ↔ |4〉. It is known that a linearly polarized laser field can be decomposed into two circularly polarized elements. Therefore, the electric field strength of the control field can be written as where and are the unit vectors of the right-hand circularly (RHC) and left-hand circularly (LHC) polarized basis respectively and can be expressed as and More specifically, the RHC (LHC) polarized component with the carrier frequency ω₂ is used to drive the transition |2〉 ↔ |3〉 (|3〉 ↔ |4〉), a weak incident probe pulse with right-hand circular polarization interacts with the intra-LL transition |1〉 ↔ |2〉 with the amplitude E_p and carrier frequency ω_p. The effective mass Hamiltonian for a single layer graphene (in the x–y plane) in the absence of an external optical field and under the magnetic field Bẑ (perpendicular to the plane of graphene) can be given by:

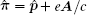
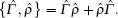
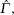
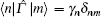
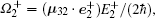
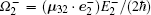
Now, we consider a medium of length L composed of the above described graphene system immersed in ring cavity.^[24] Under slowly varying envelop approximation, the dynamic response of the probe beam is governed by Maxwell’s equations:

Now some numerical studies under the steady-state conditions are shown in Figs. 2–5. It is noted that the carrier frequency of the probe field can be estimated to be approximately the same as the transition frequency which is on the order of ω₂₁ ∼ 2.39 × 10¹³ s⁻¹ for graphene at a magnetic field of B = 1 T.^[58–64] When the magnetic field reaches up to 5 T the transition frequency is estimated to be ω₂₁ ∼ 5.34 × 10¹³ s⁻¹. In the present work, taking the magnetic field B = 3 T and ω_c =10¹⁴ s⁻¹, it is confirmed that the bistable curve is located within the infrared region. According to the numerical estimate based on Refs. [58], [59], and [67] we can take a reasonable value for the decay rate γ₂ = 3 × 10¹³ s⁻¹, and assuming γ₄ = γ₃ = γ₂ these values depend on the sample quality and the substrate used in the experiment.^[58–61] Besides, the dipole moment between the transitions |1〉 ↔ |2〉 in the graphene has a magnitude on the order The electron concentration is N ≃ 5 × 10¹² cm⁻² and the substrate dielectric constant is ε_r ≃ 4.5.^[67–70] The dependence of the optical bistability on RHC signal in the absence of LHC field is shown in Fig. 2(a).

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Plots of output filed versus input field for different values of (a) RHC field and (b) detuning of RHC field. The selected parameters are γ2 = 3 × 1013 s−1, γ4 = γ3 = γ2, Δp = 0, Δ3 = 0, N ≃ 5 × 1012 cm−2, L = 90 nm, and εr ≃ 4.5.

It is found that increasing RHC field leads to a significant decrease of the bistable threshold. Physically, in the absence of LHC signal the LLs |1〉, |2〉, and |3〉 constitute a usual ladder-type configuration which owns the property of the EIT. Therefore, increasing the RHC field between LLs |2〉 and |3〉 dramatically reduces the absorption for probe light which makes the cavity field easier to reach saturation. The effect of frequency detuning of the RHC field on input–output field intensity is displayed in Fig. 2(a). It can be seen that in the nonresonance condition of RHC field, i.e. Δ_c = ±3γ₂, the optical bistability is converted into the optical multistability. The reason for the existence of OM is that y in Eq. (5) is not a cubic polynomial of the variable x in certain parameter regimes. Thus, the detuning of RHC signal can influence the absorption, dispersion and Kerr nonlinearity of the graphene medium which leads to the appearance of OM. It is profitable to note that the second term on the righthand side of Eq. (5), namely f (x) ≡ −iCρ₂₁(x), is essential for OB or OM to take place. The form of f (x) shows the Kerr nonlinearity and complicated dependences of absorption and dispersion on various system parameters including frequency detuning and intensity of coupling field. For OB, f (x) is a linear and quadratic polynomial in x, while for OM, f (x) is not a linear nor quadratic polynomial in x (the explicit expression of f (x) is so complicated that it will not be presented here). The effects of both RHC and LHC signal fields on output-input intensity field are shown in Fig. 3(a).

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Plots of output filed versus input field for different values of (a) RHC and LHC fields and (b) detunings of RHC and LHC field. The other parameters are same as those in Fig. 2.

We find that when two coupling fields (RHC and LHC) are on, the threshold of optical bistability increases due to enhancing the absorption spectrum in the presence of LHC field. Physically, the presence of LHC field between LLs |3〉 and |4〉 dramatically enhances the absorption for probe field which makes the cavity field harder to reach saturation. However, by increasing the both values of RHC and LHC fields, the thresholds of bistability reduce respectively. In this case, the effects of frequency detuning of RHC and LHC fields on output–input intensity fields are demonstrated in Fig. 3(b). It is found that the threshold and hysteresis cycle shape change obviously due to the variational frequency detunings of the RHC and LHC fields. The reason for the above result can be qualitatively explained as follows. The variational frequency detunings of RHC and LHC fields can dramatically modify the absorption, dispersion and Kerr nonlinearity of the graphene sample. So, we can see that the variational frequency detuning of coupling field leads to changing the threshold of OM. The dependences of output–input intensity fields in the resonance and nonresonance conditions of probe light are displayed in Fig. 4.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Plots of output filed versus input field for different values of (a) resonance condition of probe light and (b) nonresonance condition of probe light. The selected parameters are γ2 = 3 × 1013 s−1, γ4 = γ3 = γ2, Δp = Δ2 = Δ3 = 0, N ≃ 5 × 1012 cm−2, L = 90 nm, and εr ≃ 4.5.

It can be seen that for resonance condition (Δ_p = 0), the thresholds of OB vanish for strong RHC and weak LHC fields, while thresholds of OB increase for weak RHC and strong LHC fields. In other words, the intensity threshold of OB increases when we enhance the LHC field and reduce the RHC field. However, in nonresonance condition of weak probe light, changing the intensities of RHC and LHC signals leads to converting the OB into OM. The effects of frequency detuning of RHC and LHC fields on output–input intensity field for two cases and are shown in Fig. 5.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Plots of output filed versus input field for different values of detuning of RHC and LHC fields. (a) and (b) . The other parameters are same as those in Fig. 2.

It can be seen that for enhancing the frequency detuning leads to increasing the threshold of OB and for and enhancing the frequency detuning leads to switching from OM to OB. At the end, the effects of the electron concentration N and length of graphene sample on the output–input intensity field are depicted in Figs. 6(a) and 6(b), respectively.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Plots of output filed versus input field for different values of (a) electron concentration and (b) length of graphene sample. The selected parameters for (a) are Δp = Δ2 = Δ3 = 0 and and for (b) are Δp = 5γ2, Δ2 = Δ3 = 0, and The other selected parameters are as those in Fig. 2.

It can be easily seen that reducing the electron concentration N and graphene sample length leads to reducing OB and OM intensity threshold. Physically, reducing the electron concentration N and graphene sample length makes the cavity field easier to reach saturation, therefore the thresholds of OB and OM decrease due to reducing the absorption of weak probe light. We can see that even for L=30nm of sample length the OM is converted into OB. This is very interesting results for controlling the OM and OB in optical devices on a nano scale. Before ending this paper, we give some explanations about our work as follows. In fact, Like the laser-driven atomic medium or ensemble consisting of many single atoms,^[71] here we only consider a graphene monolayer in the graphene ensemble interacting with optical fields for the sake of simplification of the calculation. It should be emphasized that the optical conductivity of a graphene layer is proportional to its effective thickness or surface density of atoms.^[72,73] In spite of the fact that the effective thickness of a graphene layer is around one angstrom and the vacuum wavelength of the optical waves under consideration is around one micron through our calculation and analysis, it is possible to observe such behaviors by making use of the graphene ensemble. In view of rapid advance in graphene material, we believe that the realization of optical bistability will be accessible experimentally in the near future.

In this work, we theoretically investigate the optical bistability and multistability in a four-level graphene system under strong magnetic field. By manipulating the absorption and nonlinear optical properties of this optical system via the quantum interference created by RHC and LHC fields, the optical bistability and multistability can be controlled by changing the frequency detuning of optical field. The effects of electron concentration and the length of graphene sample on the OB and OM are also discussed. we find that with these different physical parameters, one can build more efficient all-optical switches and logic gate devices on a nano scale for optical computing and quantum information processing.