† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61402485, 61303061, and 71201169).
The comparison of networks with different orders strongly depends on the stability analysis of graph features in evolving systems. In this paper, we rigorously investigate the stability of the weighted spectral distribution (i.e., a spectral graph feature) as the network order increases. First, we use deterministic scale-free networks generated by a pseudo tree-like model to derive the precise formula of the spectral feature, and then analyze the stability of the spectral feature based on the precise formula. Except for the scale-free feature, the pseudo tree-like model exhibits the hierarchical and small-world structures of complex networks. The stability analysis is useful for the classification of networks with different orders and the similarity analysis of networks that may belong to the same evolving system.
The order (defined as the number of nodes) of many scale-free networks grows over time, e.g., social networks, airport networks, and Internet topologies.[1] Thus, it is inevitable to compare networks with different orders for the study of these evolving systems. Network comparison has been widely used for the classification and similarity analysis of diverse networks. Specifically, the comparison of networks with different orders strongly depends on the stability features of the evolving systems. This paper focuses on the stability analysis of a spectral graph feature of scale-free evolving systems, i.e., the weighted spectral distribution (WSD).
Graph spectra incorporate all eigenvalues of graph matrices, including adjacency and normalized Laplacian matrices. The natural connectivity is a spectral graph feature defined on the adjacency spectrum.[2] Moreover, Wu et al.[3] rigorously demonstrated that the feature is asymptotically independent of the order of regular graphs in which each node has an identical expected degree. However, our recent work[4,5] found numerically that the stability of the natural connectivity does not work in scale-free networks. The WSD is another spectral graph feature defined on the normalized Laplacian spectrum that strongly corresponds to the distribution of random N-cycles in a network.[6] Fay et al.[7] designed a calculation algorithm for the WSD using Sylvester’s law of inertia which is restricted to networks with less than 30000 nodes. Using 4-cycle structures, Jiao et al.[4] proposed a fast algorithm by which the WSD can be accurately calculated in scale-free networks with more than millions of nodes. The WSD captures the local connectivity of diverse networks.[8,9] Additionally, Jiao et al.[5] numerically observed that the WSD increases sublinearly with the network order in a stochastic scale-free network model. However, the stochastic models are not suitable for the rigorous analysis of the WSD’s stability since it is impossible to derive the WSD’s precise formula in these models. Therefore, there is a need to rigorously investigate the stability of the WSD for better understanding the performance of the spectral graph feature in evolving scale-free networks.
In contrast to stochastic models, deterministic models help us to understand the construction rules embedded in randomized structures and allow for rigorous computation of many graph features, e.g., clustering coefficients, diameter, betweenness, path length, and mean first-passage time.[10–20] The primary deterministic scale-free model was proposed by Barabasi et al.[19] However, this model lacks the small-world effect that exists in most real networks, i.e., its clustering coefficient is too small while the average length path remains relatively large. To remedy this weakness, Chen et al.[20] constructed a pseudo tree-like (PTL) deterministic model having both the small-world and the scale-free characteristics. Moreover, in Chen’s model,[20] the distribution of clustering coefficients C(k) with respect to degree k has the power-law form C(k) ∝ k−1 which exists in most hierarchical systems.[21] Therefore, our contribution includes the rigorous analysis of the WSD’s stability using Chen’s deterministic model.
Let G = (V,E) be a simple and undirected graph, where V and E are the node set and the edge set, respectively. Let dv be the degree of a node v in graph G. Then, the normalized Laplacian matrix of graph G can be expressed as[6]
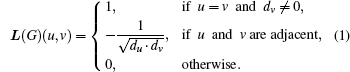
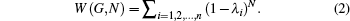
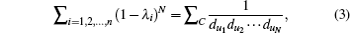
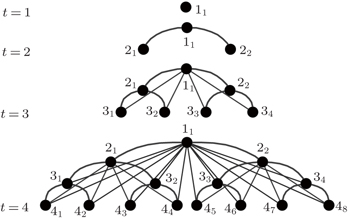
Let Tn+1 denote the n + 1 hierarchical-level graph generated by the PTL model. Specifically, Tn+1 is generated recursively with level t increased from 1 to n + 1 as follows (Fig.
At t = 1, start with a single node 11, which is the main root of the whole network.
At t = 2, two leaf nodes 21 and 22 are added and connected to the main root 11.
At t = 3, four leaf nodes 31–34 are added and each node 3j (1 ≤ j ≤ 4) is connected to the main root 11 and the subordinate root 21 (for j = 1, 2) or 22 (for j = 3, 4).
In general, at level t ∈ {1,2,…,n + 1}, 2t−1 leaf nodes tj (1 ≤ j ≤ 2t−1) are added and each node tj is connected to its t − 1 roots (t − k)⌈j/2k⌉ (k = 1,2,…,t − 1), where ⌈x⌉ rounds the value of x to the nearest integer towards infinity.
Chen et al.[20] demonstrated that the PTL model has the scale-free, the small-world, and the hierarchical characteristics of most complex networks.
Equations (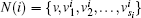
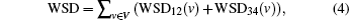

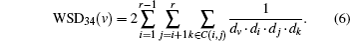
According to Eqs. (
At level t (1 ≤ t ≤ n + 1) of Tn+1, 2t−1 nodes t1,t2,…,t2t−1 are attached to other nodes in the same manner, i.e., node t1 is equivalent to each node of other 2t−1 − 1 nodes at level t. Hence, we only consider the neighbor set (i.e., N(t1)) of node t1 and the common neighbor set (i.e., C(t1,sk) = N(t1) ∩ N(sk)) of two nodes t1 and sk(≠ t1), where 1 ≤ s ≤ n + 1 and 1 ≤ k ≤ 2s−1. Without loss of generality, we assume s ≥ t.
According to the construction rules listed in Subsection 2.2,
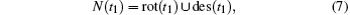
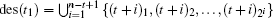
If sk is a descendant of node t1, des(sk) ⊆ des(t1) and t1 is one root of node sk (i.e., rot(sk) = rot(t1) ∪ {t1} ∪ (rot(sk) ∩ des(t1))). For this case,
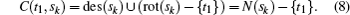
If sk (s ≥ t) is not a descendant of node t1, des(sk) ∩ (des(t1) ∪ rot(t1)) = Φ and rot(sk) ∩ des(t1) = Φ. For this case,

Specifically, N(sk) = rot(sk) ∪ des(sk), where rot(sk) includes all roots of node sk and des(sk) includes all descendants of node sk.
In Tn+1, the network order can be expressed as
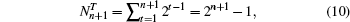

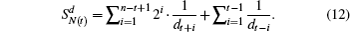

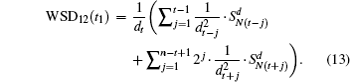
Let 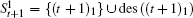
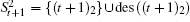
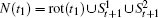
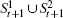
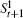
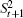

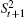
Let PN(t1) denote the set of all pairs of nodes in N(t1), where for ∀i, j ∈ N(t1) ∧ i ≠ j, (i, j) and (j,i) are two different node pairs. Then, 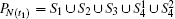
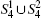

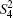
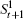
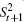
According to Eq. (
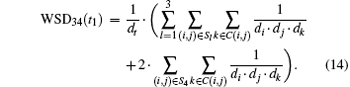
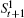



For each pair of nodes (i.e., (i1, j1) with 1 ≤ i, j ≤ t − 1) in rot(t1) = {(t − 1)1, (t − 2)1, …,11}, if i < j, node j1 is a descendant of node i1. According to Eq. (
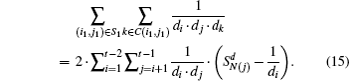
According to Eq. (
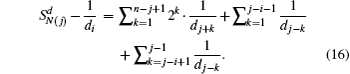
For each pair of nodes (i1, (t + j)l) with i1 ∈ rot(t1) = {(t − 1)1, (t − 2)1,…,11} and 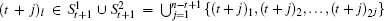

For each pair of nodes ((t + i)x, (t + j)y) with 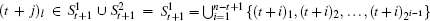
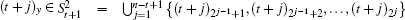
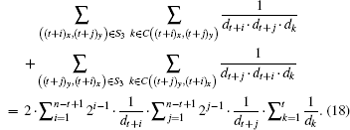
Let 


Due to the equivalence between 
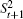
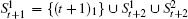


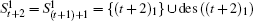
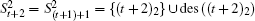

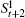

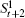
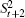
As is well known,
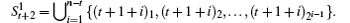

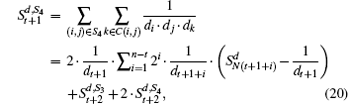

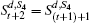
According to Eq. (
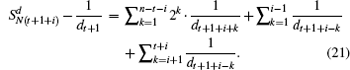

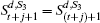
In Tn+1, node set 
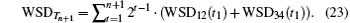
Using Eqs. (
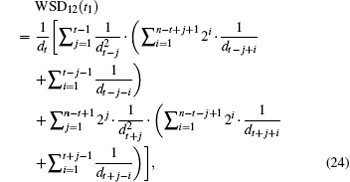
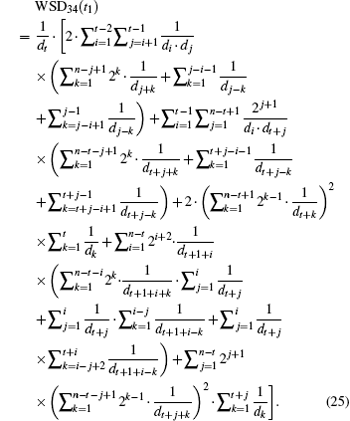
Equation (
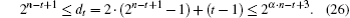
With increasing t, φ(t) = t − 1 monotonically increases and ψ(t) = 2α·n−t+1 monotonically decreases. For ∀α > 1, φ (n + 1) = n ≤ ψ (n + 1) = 2(α−1)·n with n → + ∞. Hence, for ∀t ∈ {1,2,…,n + 1}, with n → + ∞, φ(t) ≤ ψ(t) (i.e., t − 1 ≤ 2α·n−t+1). That is, dt ≤ 2 · (2n−t+1 − 1) + 2α·n−t+1 ≤ 3 · 2α·n−t+1 ≤ 2α·n−t+3. The proof is completed.
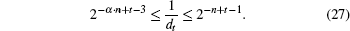
If 1/dt(t ∈ {1,2,…,n}) of Eqs. (
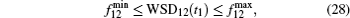
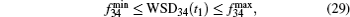

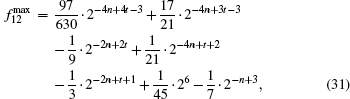
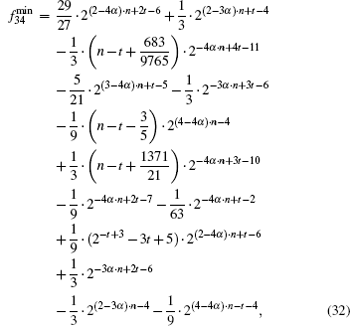

With α → 1, we can obtain
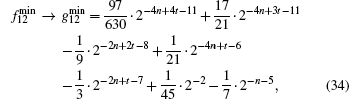

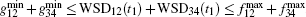
Using Eq. (
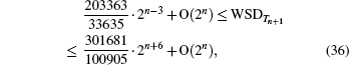
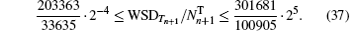

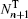
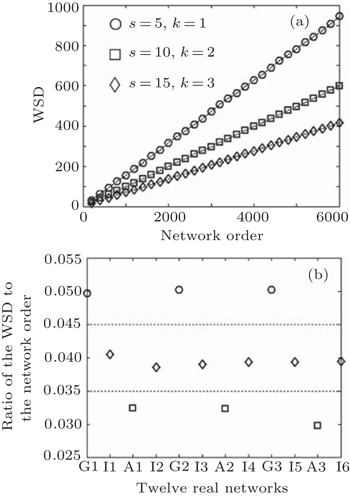
The classification of networks with different orders is an important application of the stability features embedded in evolving systems. This section first selects several simulated and real-world networks with different orders, and then classifies these networks into diverse evolving systems using the WSD’s stability.
The primary scale-free stochastic model was proposed by Barabasi and Albert.[24] At each time step of the model’s growth process, a new node is attached to m different old nodes that are already present in the existing system. Furthermore, Zou et al.[25] constructed another scale-free stochastic model that is an extension of Barabasi–Albert model. Specifically, the newly added node at each time step of Barabasi–Albert model is replaced by a newly added module generated by Watts–Strogatz model[26] in Zou’s model. The module shows the morphology feature of many real networks,[25] thus we select Zou’s model to generate diverse simulated networks.
The module generated by Watts–Strogatz model includes s nodes. Specifically, each node in the module is first connected with its 2k neighbors, and then each edge of the node is randomly rewired with a probability α. As shown in Fig.
Furthermore, we choose 12 real-world networks with different orders,[1] as shown in Table
| Table 1. Twelve real-world networks with different orders.[1] . |
As shown in Fig.
 | Fig. A1. All patterns of 4-cycles with start node v: (a) pattern 1, (b) pattern 2, (c) pattern 3, (d) pattern 4.[4] |
Our recent work[4,5] numerically verifies that the WSD increases sublinearly in a stochastic evolving scale-free network model as the network order increases. However, the stochastic models using interactive growth mechanisms are not suitable for the rigorous analysis of the scaling feature of the WSD. In this paper, our contributions focus on the derivation of the WSD’s precise formula in a deterministic model which captures the scale-free, small-world, and hierarchical features of many real-world networks. The precise formula rigorously explains the WSD’s stability (i.e., the ratio of the WSD to the network order is bounded as the network order increases). The stability indicates that the WSD can be applied to compare different order networks and to distinguish diverse evolving systems whose network orders grow over time.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |