Resonant tunneling characteristics in resonant tunneling diodes (RTD) have become an attractive research area from both theoretical and technological points of view.^[1] Survey of the electronic transport properties of nanoscale systems has a significant importance in the development of high-speed and high-frequency devices such as power memory cells, high speed logic and adders, diodes and quantum integrate circuits.^[2] To clearly understand the dynamics characteristics of nanoscale devices, quantum transport models should be considered.^[3] Wigner function method,^[4] the kinetic Monte Carlo method,^[5] the transfer matrix method (TMM),^[6] and the non-equilibrium Green’s function (NEGF) method^[7,8] are extensively used methods for modeling of transport in these devices.

Among the different quantum formalisms developed during the last decades,^[9] non-equilibrium Green’s function method initiated by the works of Keldysh, Kadanoff, Baym, and Schwinger^[7,8] stands as one of the most powerful and general approach. It provides a qualitative comprehension of quantum transport by allowing the inclusion of scattering mechanisms, contact and gate couplings. The NEGF method has been applied successfully to a great variety of systems ranging from phonon transport,^[10–13] spin transport,^[14–19] to electron dynamics in metals,^[20–22] organic molecules and fullerenes,^[23–27] and semiconductor nanostructures.^[28–32] The main route in the application of NEGF formalism to finite structures^[33–37] is division of the domain into the left contact, the right contact and the channel. The effect of contacts on a device is described by a self-energy quantity, which can be viewed as an effective potential or effective Hamiltonian. Self-energy can be derived by restricting the infinite domain Green’s function into a finite region.^[36,37] In fact, this quantity is closely related to the artificial boundary conditions in the numerical solutions of NEGF.^[38,39] Different numerical discretizations of the Hamiltonian of quantum device are possible, such as finite difference method (FDM) and finite element method (FEM), in which self-energy takes on different forms.^[40]

Semiconductor diodes incorporating the double-barrier resonant structure are known as RTD. Resonant tunneling phenomenon allows the manufacturing of diodes with extremely high switching speeds (as high as THz region) and are therefore being studied in great detail.^[9] Besides being technologically interesting, the RTD is also important as a simple test case for different formalisms and computational schemes. Owing to advances in nanofabrication technology, it has become possible to manufacture high-quality resonant tunneling structures with a wide variety of potential shapes such as rectangular, triangular, trapezoidal and parabolic.^[41–44] Mostly in the simple model which offers an advantage for numerical calculation, the barriers are considered with rectangular form. References [45] and [46] reported the dependence of resonant tunneling characteristics on the structure parameters and external electric field in triangular double-barrier structures. Impressive progress in epitaxial growth techniques renders possible the realization of double barrier (well) structures composed of gradient and horizontal potentials by using both compositional grading and layer thickness variations. Reference [47] studied the tunability of the states of two coupled parabolic quantum wells whereas Shen and Rustgi^[48] have also taken into account the effect of an electric field. Despite several works having been devoted to the search of rectangular double-barrier (RDB) structure and coupled parabolic quantum wells, to the best of our knowledge, no effort has been paid to the resonant tunneling characteristics of inverse parabolic double-barrier (IPDB) structure. The parabolic barrier is of particular importance in chemical and physical problems because it stands as a realistic representation of a real barrier, at least when tunneling involves only the upper part of the barrier. This is due to the fact that any curve with a finite radius of curvature can be approximated by a parabola over a limited range.^[49] Therefore, in this paper, we address ourselves to survey the transmission probability in IPDB structure. The effects of the external electric field and the structural parameters are investigated in details. This type of barrier model is found suitable to parameterize nuclear fission barriers^[50] and can constitute an example for the resonant tunneling diodes.

The outline of the rest of this paper is as follows. In Section 2, we present the model and methodology used throughout the work. Numerical results are given in Section 3 and finally Section 4 summarizes our conclusions.

We consider an inverse parabolic double-barrier structure, whose well of width L_W is located between two inverse parabolic barriers defined by widths W_L and W_R associated with the left and right barrier, respectively. As depicted in Fig. 1, L_i (i: 1 − 4) denotes the position of each region constituting the structure whereas the height of the left and right barrier is shown as V_L and V_R, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic representation of the device considered in this work. The solid line represents the potential profile of symmetrical IPDB structure and dashed lines stands for case when the electric field is applied.

To establish the non-equilibrium Green’s function formalism based on finite difference discretization, we describe one-dimensional Schrödinger equation for a device consisting of an active area connected to two semi-infinite contacts as follows:

2.1. Non-equilibrium Green’s function formalism

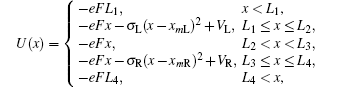
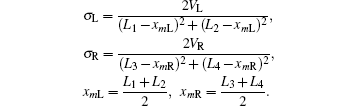
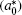
Here we briefly overview the NEGF approach based on finite difference method (FDM-NEGF) to calculate transmission coefficient and density of states. The method inquires to find the retarded Green’s function of the system G. Assuming the device region is divided into N grid points with uniform spacing, Δx̃, finite difference discretization on the one-dimensional grid is applied to the dimensionless Schrödinger equation (Eq. (2)) at each node n as follows:^[36]

Here, t̃ = 1/(2(Δx̃)²) represents the interaction between the nearest neighbor grid points n and n + 1 where abbreviation Ũ_n stands for Ũ(x̃_n).

The coupling of the device to the left and right contacts is taken into account by rewriting Eq. (2) for n = 1 and n = N with open boundary conditions expressed at the two ends.^[36] Including self-energies and considering matrix representations, the final form of Eq. (2) becomes

where [H] is the N × N Hamiltonian matrix of the device region, [I] is the N × N identity matrix, {ψ} is the wave function N × 1 vector, and {S} is N × 1 vector. [Σ_L] and [Σ_R] are N × N matrices corresponding to the self-energies of the left and right contacts, respectively. Accordingly, [H] takes a tridiagonal form as

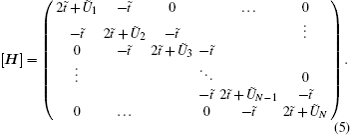
In addition, self-energy terms [Σ_L], [Σ_R] and source term {S} are given by

where and are the wave vectors of the plane wave functions in the left and right contact, respectively. The formal solution of Eq. (2) is simply given by {ψ} = [G(Ẽ)]{S}. Here [G(Ẽ)] represents N × N retarded Green’s function,

where η is an infinitesimally small positive number.

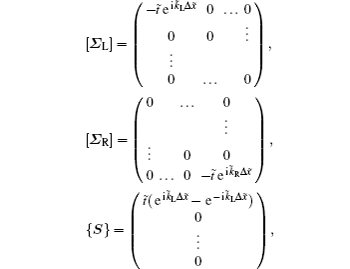
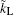
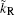
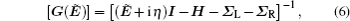
Finally, transmission coefficient T(Ẽ) can be computed as follows:

where and are referred to as broadening functions. Furthermore, density of states (DOS) at energy Ẽ can be computed using the following equation:

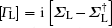
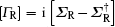
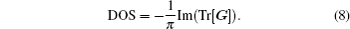
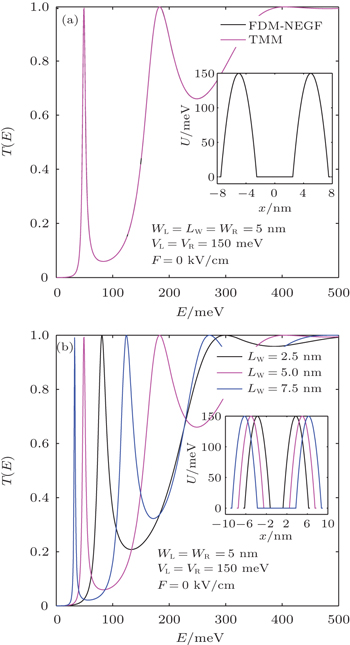
To study the transmission coefficient (T(E)) in inverse parabolic double-barrier structure, we assume the effective mass of the electron 0.067m₀ (m₀ is free-electron mass) to be constant through the system. In Fig. 2, transmission coefficient for a potentially symmetric IPDB structure is presented for a case where width of barriers (W_L,R) and well (L_W) are chosen as 5 nm and height of the barriers is set to V_L = V_L = 150 meV in the absence of external electric field. Numerical calculation of T(E) has been performed by using the TMM and FDM-NEGF methods. Figure 2(a) exposes the complete matching between the results obtained by both methods for all ranges of energies. Because of its mastery in a full quantum mechanical simulation of electronic transport, including scattering mechanisms and contact/gate coupling, in the other figures plotted we present only the results obtained by using FDM-NEGF method.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Transmission coefficient of potentially symmetric IPDB as a function of electron energy calculated by using TMM and FDM-NEGF methods for constant LW = 5 nm. (b) Variation of the transmission coefficient with respect to well width. In both subfigures we use WL = WR = 5 nm, VL = VR = 150 meV.

It is seen from the figure that the transmission coefficient exhibits resonant peaks and valleys. The first peak in transmission coefficient corresponds to the resonant tunneling associated with the fundamental quasi-bound state energy and is unity. Figure 2(b) shows the calculated transmission coefficient as a function of incident electron energy for several well widths, i.e., 2.5, 5 and 7.5 nm, for the same width and height of the barriers as shown in Fig. 2(a). Insets in all the figures of the present work demonstrate the potential profile of the IPDB structure. The results reveal that widening in well causes sharper unity resonant tunneling peak and shifting to the lower energy region. We should note the existence of a second unity resonant peak which is a reflection of the existence of a second quasi-bound state for well width of L_W = 7.5 nm. These findings show that the shift in the resonant energy is sensitive to the width of well.

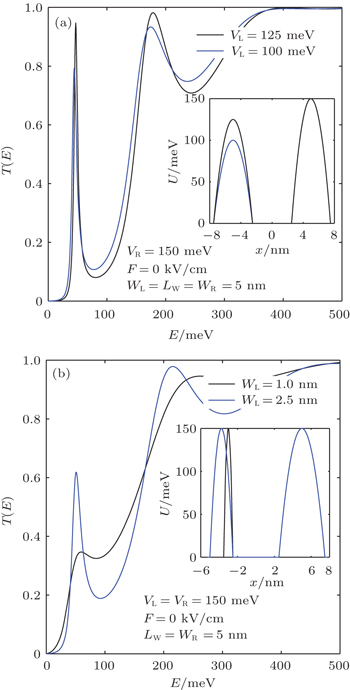
In resonant tunneling structures, general symmetry plays a central role in the resonance while asymmetry causes reduction in the heights of the transmission peaks at resonance energies.^[51] In the light of this knowledge, in Fig. 3 we present the effect of asymmetry caused by the change in the height (Fig. 3(a)) and in the width (Fig. 3(b)) of the left barrier. Height and width of the right barrier is kept constant at V_R = 150 meV and W_R = 5 nm, respectively. It is clearly seen that for asymmetrical IPDBs, the resonant tunneling occurs with a transmission peak less than unity. We have also observed that it has no importance on the T(E), of whichever barrier’s symmetry is destroyed. The main dedication from the figure is the higher (or thicker) left barrier the greater resonant peak amplitude. Similar observation has been reported by Ohmukai^[52] in RDB structure.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Transmission coefficient as a function of electron energy calculated for two different (a) height asymmetries (VL = 100 meV and VL = 125 meV) and (b) thickness asymmetries (WL = 1 nm and WL = 2.5 nm). We set LW = WR = 5 nm and VR = 150 meV.

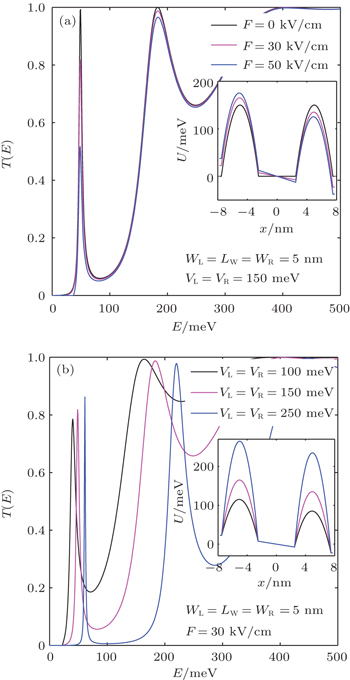
Investigation of resonance conditions taking into account effect of an external electric field has a crucial role for realistic device designing.^[53,54] The influence of an electric field turns up in a respect of breaking the symmetry of the resonant tunneling structure. Several works reported that the value of the transmission coefficient is reduced when an electric field is applied to symmetrical RDB structures and optimum transmission coefficient could be achieved in properly optimized asymmetrical structures. In this part of our work, we examine the dependence of the T(E) on the electric field as depicted in Fig. 4. The widths and heights of the barriers are set as W_L = W_R = 5 nm and V_L = V_R = 150 meV, respectively, and L_W is 5 nm. In Fig. 4(a) transmission coefficients for three different values of the electric field (F = 0, 30, 50 kV/cm) are presented. We see that the potential is no longer constant inside the barriers when a field is applied and the transmission coefficient is no longer unity even under resonant tunneling conditions. Resonant tunneling phenomenon occurs relatively at lower energy (even it is not clearly evident from the figure) and the transmission peak value decreases with increasing electric field. Figure 4(b) exhibits the effect of barrier heights on the T(E) for a constant value of electric field. We see that with the increment of the barrier height the confinement in the well is made stronger. This situation leads to a shift in the position of the transmission peak and yields the observation of a sharper resonant peak. Despite the existence of an electric field, transmission probability increases and shifts toward higher energies. This is due to the fact that more energy is required for the electron to pass through a barrier with higher amplitude. This characteristic is similar to the rectangular and triangular double-barriers structures.^[53,55]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Dependence of the transmission coefficient on the varying values of the (a) electric field at VL = VR = 150 meV, and (b) height of the barriers at F = 30 kV/cm. In both subfigures we set WL = LW = WR = 5 nm.

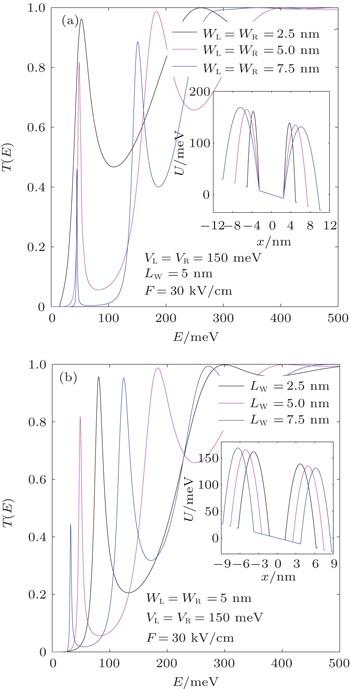
In order to expose the effect of structure parameters, considering the existence of external electric field (F = 30 kV/cm), in Fig. 5 we present the variation of transmission coefficient for several values of barrier and well widths for constant barrier heights V_L = V_R = 150 meV. Figure 5(a), plotted for well width of 5 nm, reveals that the resonant peak shifts toward the lower energy region while its amplitude becomes lower with increasing barrier width. The transmission probabilities corresponding to different well widths are plotted in Fig. 5(b). We see that as the width of the well increases, narrowing in the width of resonant peak is observed at lower energies and its amplitude decreases. The prominent feature of this figure is that influence of the electric field becomes more apparent for wider wells.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Dependence of the transmission coefficient calculated by FDM-NEGF on the varying values of (a) barrier widths at LW = 5 nm, and (b) well widths at WL = WR = 5 nm. In both subfigures we set VL = VR = 150 meV and electric field is chosen to be F = 30 kV/cm.

In the following part of the study, in order to illustrate the effect of the smoothness in the potential profile, we compare the results of transmission probability in IPDB structures with RDB given in Fig. 6. In both subfigures we use W_L = W_R = 5 nm, V_L = V_R = 200 meV, and electric field of 20 kV/cm.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Comparison of the transmission coefficient in the RDB and IPDB structures for two different values of well width (a) LW = 5 nm and (b) LW = 7.5 nm. Electric field of 20 kV/cm is taken and we chose WL = WR = 5 nm and VL = VR = 200 meV.

From Fig. 6(a), we see that if the shape of the barrier is rectangular, the resonant peak shifts toward the higher energy region while it becomes sharper compared to the IPDB. Sharper resonance corresponds to a longer lifetime which can have importance in the aspect of practical applications. Nevertheless, there is not a remarkable difference in the amplitude of the resonant peak. The influence of the well width on the transmission probability for both double-barrier structures is seen from Fig. 6(b). In comparison with the left subfigure, we see that increment in well width causes a reduction in the peak position of the resonant energy as well as in its amplitude. Meanwhile, crucial feature of the figure is the emergence of a second resonant peak occurred at higher energy that is a marker on the existence of second quasi-bound state. We should emphasize the fact that the influence of the electric field is more prominent in rectangular-shaped double barrier structure. Thus, with a proper adjustment of the structure parameters and electric field desired transmission probability can be achieved.

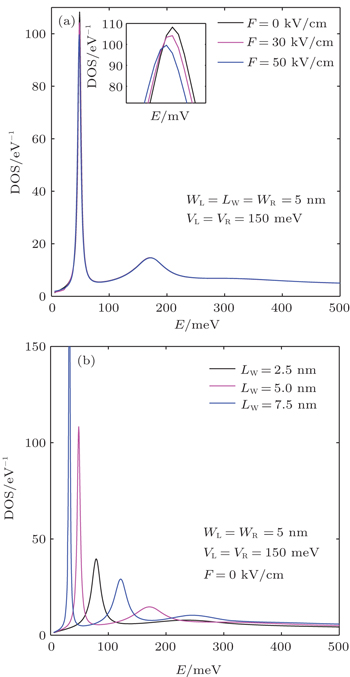
Finally, in Fig. 7(a), DOS is plotted as a function of energy for different values of electric field using the parameter set in Fig. 4(a).

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Calculated DOS as a function of energy for IPDB structure. (a) For varying electric fields for the same parameters as that in Fig. 4(a), and (b) in the absence of an electric field for different well widths with parameters used in Fig. 2(b).

It is evident that, comparatively sharper and higher peak of DOS shifts to lower energy with the increment in electric field. Besides, as seen in the inset, small variation in the peak magnitude is observed. Dependence of DOS on the well width for zero-electric field is depicted in Fig. 7(b). Widening in the well width results in red-shifting in the maximum peak whereas for wider well width second resonant peak emerges. These observations reveal that structure parameter as well as electric field modifies the DOS and this situation is consistent with the transmission coefficient results.

In this paper, we investigate the electric field-induced ballistic transport in inverse parabolic double-barrier structure. The dependence of transmission coefficient on the well width, barrier height and width is analyzed. Numerical results for tunneling transmission probability show complete matching between finite difference method-based non-equilibrium Green’s function scheme and transfer matrix method. It was found that unity transmission observed in the absence of electric field for a symmetrical composition of barriers deteriorates when the asymmetrical case turns up. A distinctive feature of the resonant energy emerges for varying widths and heights of the potential barriers in the presence of electric field. The calculated results affirmed that the structure parameters of the system and external field affect strongly the resonant tunneling characteristics and thus can be controlled by these parameters. It is believed that the results could shed light on understanding of the transport properties of resonant tunneling devices.