Recently, advances in nano fabrication techniques have made it possible to design various kinds of quantum dots with the flexibility of tuning the size, shape and number of electrons.^[1–4] There are two different strategies for creating these zero-dimensional nanostructures in a controllable and repeatable manner: “top-down” and “bottom-up” techniques.^[5,6] The top-down techniques include extreme ultraviolet or even hard x-ray lithography,^[7] electron-beam writing, or microcontact stamping,^[8] and can only create nanostructures down to the sub-100-nm range. Another method is used to efficiently guide the atoms or molecules into nanometer-scale structures through the assembly process.^[9] The reduction of dimensionality in these structures leads to the formation of discrete energy levels^[10] and subsequently drastic changes of the optical as well as many novel physical properties.^[11–13] These tunable properties of the quantum dot make it a promising candidate for various device applications, which have been extensively explored in the last few decades.^[14–19]

In addition to dimensionality, spin-dependent interactions also play an observable role in the energy spectrum formation of elecrons confined in a quantum dot.^[20–22] The coupling between the spin–moment and magnetic field which appears in the rest frame of the electron due to its motion through the electric field gives rise to Rashba spin–orbit interaction.^[23,24] In a quantum dot, the electric field can arise in two ways.^[25,26] One is from structural inversion asymmetry due to which the electric-field points towards the growth direction and restricts the motion of electrons to a two-dimensional plane. Another source of electric field is the lateral confinement potential giving rise to an in-plane electric field.^[27] If the confinement is rotationally symmetric, it will be parallel to the radius vector r = (x,y). Energy levels are directly affected by spin–orbit coupling; its influence is realized in all electronic, optical and physical properties of the system including thermodynamics.^[28,29]

There have been several experimental and theoretical studies devoted to the thermodynamic properties of quantum structures,^[30–37] but the theoretical understanding of the effect of SOI on these properties is still in its infancy. Gornik et al.^[30] have reported the first observation of magnetic-field-dependent specific heat (C_v) in quasi two-dimensional objects. Intra as well as inter-Landau level contributions to (C_v) are recognized which reveals a density of states with Gaussian broadening. Liao^[34] has investigated the heat capacity of horizontally absorbed molecules in the presence of a static electric field. The magnetization of nanoscopic quantum rings and dots has been calculated by Climente et al.^[35] A change in topology leads to a sharp response in the magnetization and thus suggesting the use of it for probing the topology of nanocrystals. Boyacioglu and Chatterjee^[36] have studied the specific heat and entropy of the GaAs quantum dot with Gaussian confinement in the presence of an external magnetic field but neglecting the spin–orbit interaction. To the best of our knowledge, no exhaustive study for the role of Rashba SOI on the thermodynamic properties of quantum dots has been made so far.

In this paper, we analyze the thermodynamic properties exhibited by a quantum dot in the simultaneous presence of a magnetic field and Rashba SOI. The approach is to first calculate the energy spectrum of the quantum dot system and then use the partition function formalism to uncover its thermodynamic behavior. We investigate the properties of a circular quantum dot carved out of a two-dimensional heterostructure in which it is assumed that electrons are strictly confined to the two-dimensional plane. Although in the physical realm, electron wave-functions have a finite spread in the perpendicular direction of this plane but the small dimension restricts the electrons to the lowest subband and all electrons exhibit exactly the same behavior in this direction. Therefore, single-particle properties are unaffected by the spreading of wave functions and our assumption sounds plausible. Here, we have incorporated the spin–orbit term only due to the parabolic confinement and therefore the system Hamiltonian is diagonal in spin space.

The paper is organized as follows. In Section 2, we present the mathematical formalism for our system. In Section 3, we analyze the numerical results obtained for a quantum dot of InSb and then conclude our findings with specific remarks in Section 4.

In order to model the confinement of charged particle within the small region of circular quantum dot of radius, the particle is assumed to be moving in a parabolic potential of the Fock–Darwin type^[38] given by

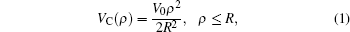
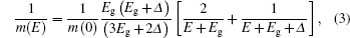
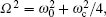
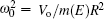
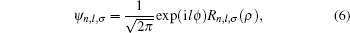
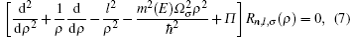
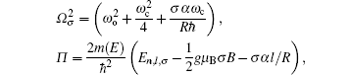
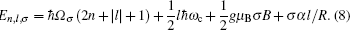
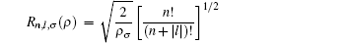
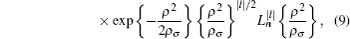
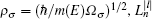
For thermodynamical calculations, we fix the external conditions of the single electron quantum dot by considering it a closed system in contact with a heat bath at temperature T. The canonical partition function giving a measure of thermally accessible energy states is defined as

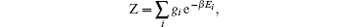
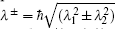
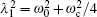
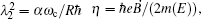
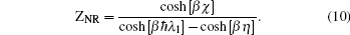
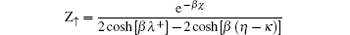
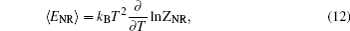
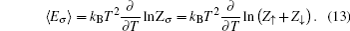
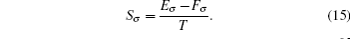
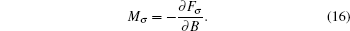
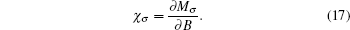
In our numerical investigation, we choose an InSb quantum dot with m(E) = 0.014m₀, E_g = 0.24 eV, Δ = 0.81 eV,^[20] and radius R = 14.8 nm. The small effective mass and high g factor of InSb make it one of the most promising materials for application in spintronics^[40] and spin-based quantum information technology.^[41] In the presence of an external magnetic field and Rashba SOI, the behavior of charged particle in a parabolic quantum dot can be described as harmonic oscillator with frequency which is a function of not only confinement potential and magnetic potential but also depends on Rashba SOI. This interaction can enhance or reduce the oscillator frequency through Ω_σ depending on the particle spin orientation. Another contribution of SOI comes from the last term of Eq. (8) which is independent of an external magnetic field. Therefore, even at zero magnetic field, it lifts the spin-degeneracy of the states with the same orbital momentum. However, states with parallel spin and l (antiparallel spin and l) remain twofold degenerate which is known as Kramer’s degeneracy.^[20,42]

In Fig. 1, the specific heat of an InSb quantum dot has been plotted as a function of the magnetic field at three different values of temperature. Rashba SOI is taken to be constant at α = 40 meV·nm. For a fixed temperature, specific heat initially rises rapidly with the increase in magnetic field, attains a maximum value and then decreases to zero. The magnitude of specific heat is directly proportional to the thermal excitations of electrons. In addition to the thermal energy k_BT, these excitations depend on the density of thermally accessible states lying a few k_BT above and below the Fermi energy level. At a particular value of magnetic field, the spin–orbit interaction provides a “crossing” of the energy levels with the same orbital momentum but different spins. This results in an enhanced density of states for the quantum dot. Therefore, specific heat peaks at this magnetic field corresponding to maximum accessible states for electrons of energy k_BT. The increase in temperature shifts this peak towards a higher magnetic field and also broadens the peak. It shows that the increase of temperature enlarges the magnetic field range in which the system can absorb maximum heat. For higher values of magnetic field, the cyclotron hω_c energy becomes much larger than the binding energy of the confining electric potential, thereby electric bound states shift to Landau-type magnetic levels. The increase in level spacing reduces the probability of excitations resulting in a decrease of absorption of heat or specific heat. We observe that at low temperatures such as T = 5 K, C_v goes to zero very rapidly whereas for T = 20 K, this fall is rather smooth.

Fig. 1.

	Figure Option ViewDownloadNew Window
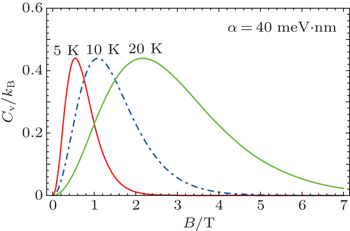	Fig. 1. Variation of specific heat of InSb quantum dot with magnetic field at temperature T = 5 K, 10 K, and 20 K with Rashba spin–orbit coupling parameter α = 40 meV·nm.

In Fig. 2, we plot the variation of specific heat with magnetic field at constant temperature for three different values of α = 0, 8 meV·nm and 40 meV·nm. Qualitatively the system shows the same variation as in the case of constant Rashba coupling parameter (α) and different temperatures. This can be explained as: with the increase in the value of Rashba coupling, the crossing between states of the same orbital momentum occurs at a higher magnetic field. It means that the density of states becomes maximum for the higher magnetic field, which effectively shifts the peak of specific heat. It is evident from Figs. 1 and 2 that in the variation of specific heat with B, the increase of either temperature or Rashba SO coupling parameter (α) results in the shifting and broadening of the peak. Therefore, we can conclude that the increase of either of the variables increases the probability of heat absorption although the mechanism is different. When the system temperature is increased, the thermal energy k_BT of electrons increases and more states become thermally accessible whereas a change in α modifies the density of states.

Fig. 2.

	Figure Option ViewDownloadNew Window
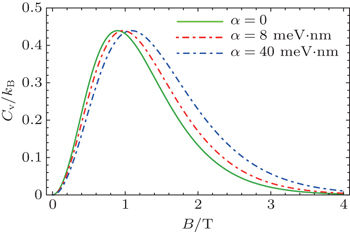	Fig. 2. Specific heat of InSb quantum dot as a function of magnetic field for different values of Rashba spin–orbit coupling parameter (α) at temperature T = 10 K.

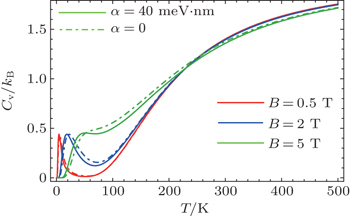
In Fig. 3, we have shown the specific heat of a quantum dot as a function of temperature for three different values of magnetic field B = 0.5 T, 2.0 T, and 5.0 T. At each magnetic field, the contribution of Rashba SOI is explicitly shown by plotting C_v with (solid line) and without (dashed line) Rashba SOI. With low magnetic fields, as the temperature is increased from absolute zero, C_v suddenly increases and then decreases giving a peak-like structure. The observed peak structure is the well-known Schottky anomaly of the heat capacity, typical for a system where only two states are of importance at low temperature because thermal energy gained by electrons is enough for only the lowest two levels. SOI sharpens the peak and shifts it to the lower value of temperature. It shows that an electron requires a smaller amount of thermal heat to be excited to the next higher level. Because SOI lifts the spin degeneracy, more energy levels are available in the unit range of energy, thereby reducing the level spacing and shifting the peak to lower thermal energy. With the further increase in temperature, specific heat starts increasing almost linearly and converges to the saturation value of 2k_B. This steady increase in C_v with temperature can be attributed to the increase in thermal energy k_BT of electrons which makes more and more states availiable for thermal excitations.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Variation of specific heat with temperature for B = 0.5 T, 2.0 T, and 5.0 T. At each magnetic field, solid and dashed lines represent the specific heat with and without Rashba SOI, respectively.

When the magnetic field is increased to 5 T, specific heat remains zero in the region where it peaks for the low magnetic fields B = 0.5 T and 2.0 T. Instead a shoulder is developed in a temperature range of 10–50 K. This can be attributed to the broadening of energy spacing between the different Landau levels in a high magnetic field. In the upper range of temperature, the behavior of specific heat is more or less the same for all the three magnetic fields and is reminiscent of 3D behavior of C_v. Electrons have sufficient thermal energy and therefore excitations have a little dependence on density of states.

In Fig. 4, we plot C_v as a function of effective Lande’s g factor at B = 5 T and temperature T = 10 K. A double-peak structure is observed irrespective of the presence of SOI. Without SOI, C_v is symmetric with respect to g = 0 where a local minima is observed. The increase in either side of g results in the increase of C_v which after attaining a maximum value decreases with further increase in g. Introduction of SOI removes the symmetry with respect to g but a double-peak structure is conserved.

Fig. 4.

	Figure Option ViewDownloadNew Window
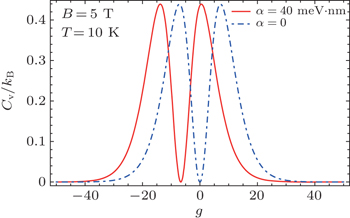	Fig. 4. Variation of specific heat with Lande’s g factor for α = 0 (blue) and α = 40 meV·nm (red) at B = 5 T and temperature T = 10 K.

Next, the thermodynamic quantity of interest on which we have studied the effect of Rashba SOI is entropy. Variation of entropy with respect to the magnetic field at temperatures T = 10 K, 50 K, and 100 K is shown in Fig. 5. In order to investigate the effect of Rashba SOI on entropy, it is customary to vary it with and without spin–orbit interaction. At any particular value of B and T, the entropy is always higher in the presence of Rashba SOI. This is because the spin–orbit interaction removes the spin degeneracy, resulting in more energy states and thus more disorder. From Fig. 5, entropy is also found to be inversely proportional to the magnetic field. As the increase in magnetic field restricts the particle motion to Landau-type levels, disorder decreases and thus entropy. We observe that for T = 10 K, the entropy reduces to zero at B = 3 T. The system is in perfect order. As magnetic field attempts to bring the system in order and temperature introduces the opposite effect, there is competition between magnetic confinement and thermal energy. Therefore, entropy decreases but never comes to zero for high values of magnetic field and temperature. Energy level spacing decreases with Rashba SOI and at T = 100 K, electrons gain enough thermal energy for intra as well as inter landau level transitions. Consequently, at this temperature, entropy becomes nearly independent of magnetic field in the presence of Rashba SOI. In Fig. 6, the variation of entropy with temperature is given for different values of α. As expected the entropy of a quantum dot increases with the increase in temperature. In the high temperature region, the variation of entropy is almost linear; however, for the low temperature, entropy develops a shoulder which becomes more and more pronounced with the increase in the value of α. The increase in entropy with temperature results from enhanced thermal energy of electrons which brings more and more disorder in the form of random motion.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Variation of entropy of InSb quantum dot with magnetic field at temperature T = 10 K, 50 K, and 100 K. At each value of T, entropy is plotted for α = 0 (dashed line) and α = 40 meV·nm (solid line).

Fig. 6.

	Figure Option ViewDownloadNew Window
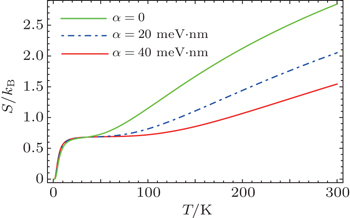	Fig. 6. Entropy as a function of temperature with different values of Rashba spin–orbit coupling parameter.

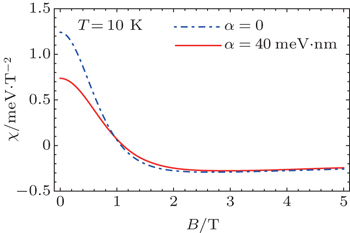
We further studied the variation of magnetization (M) and susceptibility with magnetic field. In Fig. 7, solid and dashed lines show the magnetization with and without Rashba SOI respectively. Magnetization provides the information about how the system responds to an external magnetic field. When no Rashba coupling is there, magnetization changes abruptly with a small increase in B and a positive peak is observed after which magnetization starts decreasing. With the increase in magnetic field, the occupation of a higher angular momentum state becomes energetically favorable resulting in the decrease of M. At a critical value of B, magnetization becomes equal to zero and the further increase in B leads to a change in the sign of M. In this way, a magnetic phase transition takes place from paramagnetism to diamagnetism. In the low magnetic field regime, Rashba coupling modifies the response of the system quantitatively after which it behaves in the same manner as before. These peculiarities in magnetization of the system produce well understandable features in magnetic susceptibility (χ) of quantum dot. Susceptibility which is defined as the rate of change of magnetization with respect to magnetic field is shown in Fig. 8. The effect of Rashba SOI is observed only for the low values of magnetic field.

Fig. 7.

	Figure Option ViewDownloadNew Window
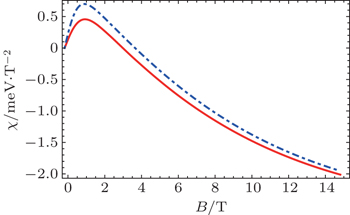	Fig. 7. Magnetization (M) of InSb quantum dot as a function of external magnetic field with α = 40 meV·nm and 0 meV·nm. Solid and dashed lines represent M with and without Rashba SOI.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Magnetic susceptibility (χ) as a function of the magnetic field at T = 10 K.

We have studied the effect of Rashba spin–orbit interaction and static magnetic field on the specific heat, entropy, magnetization and susceptibility of InSb quantum dot. An interesting interplay of Rashba spin–orbit coupling parameter, magnetic field, and temperature is observed in determining these thermodynamic properties. We observe that qualitative variation of specific heat with magnetic field is the same as the increase in either temperature or Rashba SOI. A direct consequence is that the absorption of heat by a quantum dot can be improved either with the temperature or Rashba spin–orbit coupling parameter. At low magnetic field, the variation of specific heat with temperature gives a peak-like structure. The Rashba SOI sharpens this peak and shifts it to the lower value of temperature. Entropy is found to increase with the temperature but we observe that Rashba SOI can nullify the effect of temperature. As a result, entropy can maintain a constant magnitude for a certain range of temperature. This property is useful where one requires a temperature as high as possible but entropy has to be minimum. The magnetic properties of the system are found to be more susceptible to the Rashba SOI at low values of temperature and magnetic field. These are often assumed to be intrinsic. The ability to externally control the properties of magnetic materials would be highly desirable from fundamental and technological viewpoints, particularly in view of the recent developments in magneto–electronics and spintronics.