High-order harmonics are generated when the matter is subject to a short, intense laser field.^[1] Since the high-order harmonic spectra can be extended to the soft x-ray region^[2,3] and exhibit a supercontinuous structure, it becomes a preferred light source for the generation of attosecond pulses.^[4,5] Generally, the high harmonic generation (HHG) can be well understood by the semiclassical three-step model.^[6,7] According to this model, the electron is first ionized toward continuum by tunneling through the field-modified potential barrier, then accelerated in the laser field, and finally recombined with the parent ion and emits a harmonic photon. The highest harmonic energy (cutoff) is given by the formula I_p + 3.17U_p, where I_p is the atomic ionization potential and U_p is the ponderomotive potential. Recently, the studies of plasmonic-field-enhanced HHG have demonstrated that the inhomogeneous field could considerably broaden the plateau region of HHG.^[8–16]

With the development of laser technology, an intense laser pulse that contains only a few cycles can be generated now.^[17–19] For a few-cycle laser pulse, the carrier-envelope phase (CEP) plays important roles in attosecond physics,^[20,21] HHG,^[22] above threshold ionization (ATI),^[23,24] double ionization,^[25,26] and so on. Hence, the measurement of the CEP is essentially crucial for laser–matter interaction. Jones et al.^[27 confirmed the control of the pulse-to-pulse CEP using temporal cross correlation, based on the f-to-2f scheme.^[27–30] However, the f-to-2f interferometer could not measure the absolute phase. Therefore, a variety of methods of measuring the CEP were raised. The determination of CEP using ATI spectrum has been demonstrated both experimentally^[31–34] and theoretically.^[35,36] Compared to ATI, the HHG spectrum is an all-optical method in which its signal can be more easily collected, and strong dependence of harmonic cutoff on the CEP^[37,38] suggests that the retrieving of CEP from HHG spectrum is feasible. Li et al.^[39] and Xiang et al.^[40] have proposed two methods to measure the CEP using the HHG spectrum from asymmetric molecules. Fetić et al.^[41] investigated the CEP-dependent plasmonic-field-enhanced HHG yield by using the semiclassical method. As far as we know, for the atom in the inhomogeneous field, there are no reports about the dependence of the cutoff of the HHG spectra on the CEP from the simulations by solving the time-dependent Schrödinger equation (TDSE). Thus, it is necessary to confirm the relationship between the HHG spectra and the CEP of the laser pulse by the TDSE, which will be done in this work. Based on the comparison of cutoff dependence on the CEP of laser pulse from TDSE and semiclassical simulations, we will demonstrate the possibility of measuring CEP from plasmonic-field-enhanced atomic HHG.

In Section 2, we briefly present the theory and method. In Section 3, the numerical results and analysis are presented. Finally, our conclusions are given in Section 4. The atomic units (a.u., ℏ = m_e = e = 4πε₀ = 1) are used throughout, unless otherwise stated.

In order to obtain the HHG spectrum driven by spatial inhomogeneous field, we solve the one-dimension time-dependent Schrödinger equation (1D TDSE)

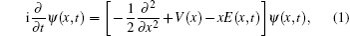
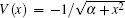
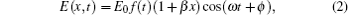
In Eq. (1), we assume that the H atom is in its ground state (initial state) before starting the time propagation. Equation (1) is solved numerically by using the Crank–Nicolson scheme.^[45] In addition, to avoid spurious reflections from the spatial boundaries, at each time step, the electron wave function is multiplied by an absorption function. Once the time-dependent wave function ψ(x,t) is determined, the time-dependent induced dipole acceleration can be given by means of Ehrenfest’s theorem

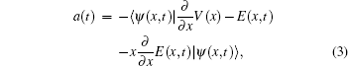
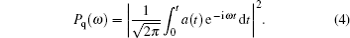
In our simulations, the intensity and wavelength of the incident laser is 3.0 × 10¹⁴ W/cm² and 800 nm, respectively. The inhomogeneity parameter is taken to be β = 0.005. We consider four different pulse durations of laser field: 3 fs, 5 fs, 8 fs, and 10 fs.

We first simulate the HHG spectra in both homogeneous field (β = 0.0) and inhomogeneous field (β = 0.005) for a CEP of ϕ = 0.0π. In Fig. 1 we show our results, from which three main characteristics are observed: the first one is that the cutoff of HHG spectra do not change by increasing the pulse duration in both fields; the second one is that the cutoff energies of the HHG in the inhomogeneous fields are extended about two times compared to the homogeneous fields; finally, for the inhomogeneous fields, HHG spectra reveal two-plateau structure for all pulse durations. These characteristics are beneficial to study the dependence of HHG cutoff position on the CEP of laser.

Fig. 1.

	Figure Option ViewDownloadNew Window
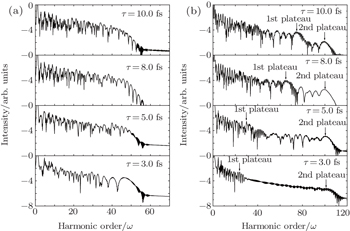	Fig. 1. The HHG spectra in (a) homogeneous field (β = 0.0) and (b) inhomogeneous field (β = 0.005) for pulse durations of 3 fs, 5 fs, 8 fs, and 10 fs with CEPs of 0.0π.

In order to study the underlying mechanism of the cutoff extension and two-plateau of HHG spectra, we perform the classical trajectory simulation by solving the Newton equation. The acceleration of electron in the inhomogeneous field E(x,t) can be written as

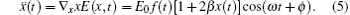
Under the initial condition that the electron velocity ionized at the time t_i from the nucleus v(t_i) = 0, and the electron recombines at the recombination t_r under x(t_r) = 0, we can obtain the kinetic energy of electron, E_k(t_r) = v²(t_r)/2. Then, the photon energy of emitted harmonic is I_p + E_k(t_r). Figure 2 shows the dependence of harmonic orders on the ionization time t_i (blue squares) and recombination time t_r (red circles) of the electron for inhomogeneous fields with different pulse duration. One can see that there are two major emission events (labeled as R₁ and R₃) for the fields with pulse durations of τ = 3.0 fs (Fig. 2(a)) and τ = 5.0 fs (Fig. 2(a)), and three major emissions (R₀, R₁, and R₃) for somewhat longer pulse durations of τ = 8.0 fs, 10 fs (Figs. 2(c) and 2(d)). For the emission of R₁, the classical energies are perfectly consistent with the cutoff of HHG spectra from TDSE simulations shown in Fig. 1.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Dependence of harmonic orders on the ionization time ti (blue squares) and recombination time tr (red circles) of the electrons in the inhomogeneous fields. (a) τ = 3 fs, (b) τ = 5 fs, (c) τ = 8 fs, (d) τ = 10 fs.

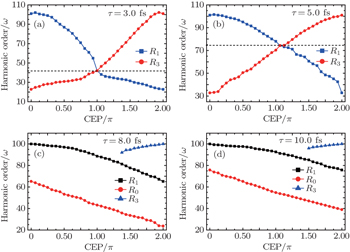
Next, we investigate the CEP dependence of the cutoffs of HHG both in the homogenous and inhomogeneous fields for different pulse durations. In Fig. 3 we present the harmonic cutoff as a function of the CEP for the homogeneous field by solving the TDSE. It is clear that the cutoffs of the HHG are determined by the CEP modulo π for the short pulse (3.0 fs and 5.0 fs). However, the cutoff position of HHG is not sensitive to the CEP with increasing pulse duration, such as in the case of 8.0 fs and 10.0 fs. This is not appropriate to determine the CEP of driving laser through the cutoff position of HHG. We carry out the classical calculation to understand the underlying physics behind these phenomena. Figures 4(a) and 4(b) show the results of the dependence of harmonic order on the recombination time and the CEP for τ = 3.0 fs and τ = 5.0 fs, respectively. Three main emissions (R₁, R₂, and R₃) are clearly displayed. For the three events, the recombination time decreases with the increase of the CEP value. In Figs. 4(c) and 4(d), we present the harmonic order as a function of the CEP for different emission events. Firstly, we can see that the harmonic order labeled by R₁ decreases monotonously by increasing the CEP value in the range from 0.0π to 1.08π, R₂ increases from 0.0π to 1.08π and then decreases from 1.08π to 2.0π, R₃ increases with the increase of the CEP value in the range from 1.08π to 2.0π. Secondly, the part above the dashed line in Figs. 4(c) and 4(d) is in agreement with the TDSE results, but the part under the dashed line in Figs. 4(c) and 4(d) is invisible in the TDSE calculation.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Dependence of the harmonic cutoff on the CEP of the homogeneous laser field from TDSE simulations for the pulse durations of τ = 3.0 fs (black squares), 5.0 fs (red circles), 8.0 fs (blue up triangle), and 10.0 fs (magenta down triangle).

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Classical harmonic order as a function of the recombination time of the electron and the CEP of the homogeneous laser pulse. (a), (c) τ = 3.0 fs; (b), (d) τ = 5.0 fs.

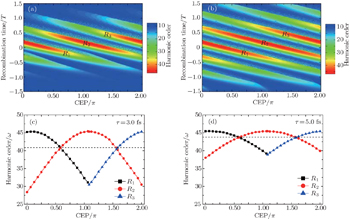
Then, we study the influence of the CEP on HHG generated in inhomogeneous fields. Figure 5 shows the classical trajectory of the electron with the change in CEP for different pulse durations. Compared with the case of homogeneous field shown in Fig. 4, we find that the emission of R₂ is suppressed in the inhomogeneous field, which results in the appearance of two-plateau structure. In addition, the cutoff energy of the HHG spectra is extended in inhomogeneous field, for example, from 46th in homogeneous field to 100th in inhomogeneous field for the case of 0.0 π, and the cutoff energy is much more sensitive to the change of ϕ. Same as the case of the homogeneous field, the recombination time of the electron decreases with the increase of the CEP value in the inhomogeneous field. Dependence of harmonic order on the CEP value is shown in Fig. 6 for the main emissions of R₁ and R₃ (to compare the results from Fetić et al.,^[41] R₁ is not show here). From the figure, we can clearly see that R₁ decreases monotonously by increasing the CEP value in the range from 0.0π to 2.0π, while R₃ increases monotonously with the increase of the CEP value from 0.0π to 2.0π. The results show that the plasmonic-field-enhanced HHG spectra depend on the CEP modulo 2.0π. Moreover, the R₁ and R₃ intersect at ϕ = 1.08π, where they have the same recombination energy. The position of the cross point is independent of the pulse duration in the horizontal direction, but harmonic orders increase in the vertical direction. The harmonic orders at the cross point with ϕ = 1.08π are 47th, 71th, 84th, and 88th for pulse durations of 3.0 fs, 5.0 fs, 8.0 fs, and 10.0 fs, respectively. If we define the modulation depth, which is the difference between the maxima and the cross point of the cutoff position of HHG spectra, we find that the modulation depth decreases with the increase of the pulse duration, but it remains big enough for the longer pulses of τ = 8.0 fs and τ = 10.0 fs. This implies that the measurement of the CEPs using the atomic HHG spectra in the inhomogeneous field is possible even for the longer pulses, while this way cannot determine the CEP in homogeneous field (see Fig. 1).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Recombination time of harmonic cutoff as a function of the CEP of the inhomogeneous laser field with pulse durations of (a) 3.0 fs, (b) 5.0 fs, (c) 8.0 fs, and (d) 10.0 fs.

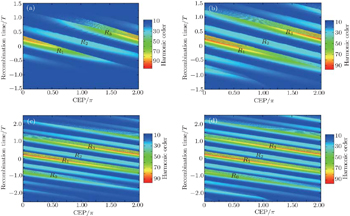
To compare the results shown in Fig. 6, in Fig. 7 we show the cutoff position of the HHG spectra as a function of the CEP value form TDSE simulations. For τ = 3.0 fs and τ = 5.0 fs, there are two events labeled R₁ and R₃ which correspond to the second and the first plateaus of HHG spectra in Fig. 1. With the increase of the CEP, the second plateau (R₁) decreases and the first plateau (R₃) increases in the range from 0.0π to 2.0π. The TDSE results are in good agreement with the classical results (see Figs. 6(a) and 6(b)), but the cross point for τ = 5.0 fs moves rightwards a little bit, compared with τ = 3.0 fs. In the case of τ = 8.0 fs (Fig. 7(c)), we can find that there are three CEP-dependent emission events R₀, R₁, and R₃. The R₀ and R₁ correspond to the first and second plateaus of HHG spectra, respectively, and they decrease monotonously by increasing the CEP value from 0.0 to 2.0π. R₃ does not appear in the CEP region of ϕ < 1.375π due to weak intensities. When ϕ > 1.375π, the cutoff position of the third plateau increases monotonously. Similar conclusion can also be obtained, except that the third plateau bursts into the HHG spectra at ϕ = 1.5π, for the pulse duration of 10 fs (Fig. 7(d)). Moreover, comparison between Figs. 6 and 7 shows that agreement between TDSE and semiclassical method is not good for the pulse durations of 8 fs and 10 fs. The reason for the difference between two simulations is that the semiclassical method does not take the interference effects between different trajectories for the longer pulses into consideration. In the case of the inhomogeneous field, because the intensity difference of the first and the second plateaus is almost an order of magnitude, it is easy to find the cutoff positions of two plateaus from the HHG spectra compared to the homogeneous field (see Fig. 1). In addition, in Figs. 7(a) and 7(b) (τ = 3.0 fs and τ = 5.0 fs), we can see that the cutoff position changes very slowly with increasing CEP in the range of 0.0π to 0.25π. That is to say, the slight change of the cutoff position will lead to a great change of the CEP. As an example, in Fig. 7(b) we analyze the difference of CEP (Δϕ) between two adjacent harmonics. For H101 and H100, Δϕ = 0.16π, this means that to experimentally determine the CEP through measuring cutoff positions of the HHG spectra with the measurement accuracy of one order will give rise to large error in the small scope ϕ ∈ [0.0π,0.25π]. However, for other range of the cutoff position, the difference of CEP (Δϕ) between two adjacent harmonic orders is about only 0.02π (Δϕ ≈ 0.02π), this indicates that the error of the determination of the CEP is very small for ϕ > 0.25π, even if the measurement error of the cutoff position is one order. At present, the measurement error of the HHG is generally less than one order in the experiment. Therefore, it is practicable to determine the CEP based on the cutoff position of HHG spectra in inhomogeneous field. Based on the results of solving TDSE, we confirm that the cutoff positions of the first and second plateaus are very sensitive to the variation of the CEP in the range of 0.0π ≤ ϕ ≤ 2.0π, even for the case of the pulse duration τ = 8.0 fs and 10 fs, which are suitable for determining the CEP of driving laser pulse.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Harmonic order as a function of the CEP of the laser pulse for the classical simulation in the inhomogeneous filed β = 0.005: (a) τ = 3.0 fs, (b) τ = 5.0 fs, (c) τ = 8.0 fs, (d) τ = 10.0 fs.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The same as Fig. 6 but from TDSE calculations.

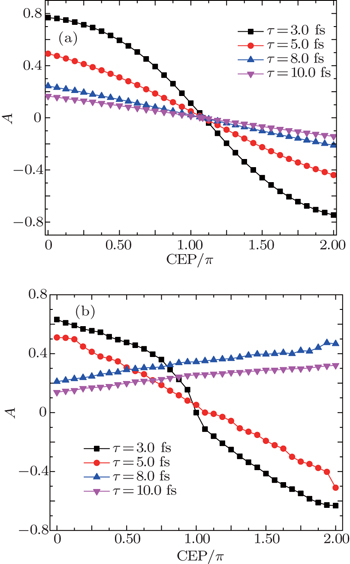
Finally, in order to determine the CEP of the driving laser pulse conveniently, we define a parameter A to describe the dependence of harmonic cutoff on the CEP value of the laser pulse, which is written as

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The parameter A as a function of the CEP in the inhomogeneous filed. (a) Classical results; (b) TDSE results.

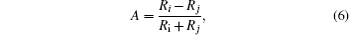
In conclusion, we have investigated the CEP control of the plasmonic-field-enhanced HHG of H atom by solving the TDSE numerically and the semiclassical simulation. We find that there are two plateaus of the HHG spectra in the inhomogeneous field. By means of the semiclassical simulation, we explain the origin of these phenomena. The results of the semiclassical simulation are in good agreement with the TDSE results. For the longer laser pulses τ = 8.0 fs and τ = 10.0 fs, the third plateau bursts into the HHG spectrum at ϕ = 1.375π. For ϕ > 1.375π, the cutoff position of the third plateau increases in the range of 1.375π to 2.0π. Contrary to the dependence of the HHG cutoff on the CEP with a period of π in homogeneous field, the HHG spectrum depends on the CEP modulo 2.0π in the inhomogeneous field. The position of the cutoff of the HHG spectrum are dramatically affected by the CEP for the inhomogeneous field even in a little longer pulse. Moreover, the results for the first and the second cutoff of the HHG spectra with the CEP obtained from both semiclassical and the TDSE method have the same behavious in the case of short pulse. However, for the longer pulses τ = 8.0 fs and τ = 10.0 fs, the results of the TDSE are different from the semiclassical simulation. The TDSE results show that the cutoff positions of the first and second plateau decrease monotonously with the increase of CEP. As a result, the CEP of the laser pulse can be controlled effectively by the plasmonic-field-enhanced HHG spectrum, which provides a useful method for measuring the CEP of few-cycle laser pulses.