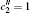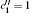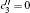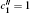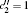† Corresponding author. E-mail:
Project supported by the Egyptian Ministry of Scientific Research (Project No. 24-2-12).
A tetrad field that is homogeneous and anisotropic which contains two unknown functions A(t) and B(t) of cosmic time is applied to the field equations of f (T), where T is the torsion scalar, T = TμνρSμνρ. We calculate the equation of continuity and rewrite it as a product of two brackets, the first is a function of f (T) and the second is a function of the two unknowns A(t) and B(t). We use two different relations between the two unknown functions A(t) and B(t) in the second bracket to solve it. Both of these relations give constant scalar torsion and solutions coincide with the de Sitter one. So, another assumption related to the contents of the matter fields is postulated. This assumption enables us to drive a solution with a non-constant value of the scalar torsion and a form of f (T) which represents ΛCDM.
Recently, it has been found that there is a contradiction between cosmological observations and Friedmann–Robertson–Walker (FRW) cosmology. The observations show that the universe is in an accelerating expansion era, but the FRW cosmology of Einstein’s general relativity (GR) shows that it is not. This accelerating expansion of the universe is suggested to be due to a mysterious type of energy with negative pressure that is known as dark energy (DE). The evidence of the existence of this type of energy comes from the observation of supernovae type Ia,[1–7] cosmic microwave background (CMB) anisotropies measured with Wilkinson microwave anisotropy probe (WMAP),[8] and the large scale structures.[9–11] These observations suggest that more than two-thirds of our universe consists of DE and the remaining consists of relativistic dark matter and baryons.[12]
Modified theories of gravity have gained a lot of interest because of their possible explanation of DE.[13,14] This unknown energy, DE, which has negative pressure, may be physically equivalent to vacuum energy and is almost equally distributed in the universe. It has been used as an ingredient factor in a recent attempt to formulate a cyclic model of the universe. In its developing process, the universe passes through several eras corresponding to several values of ω which is the parameter of the equation of state (p = ωρ): the stiff fluid era (ω = 1), the radiation dominated era (ω = 1/3), the dust dominated era (ω = 0), and the transition era (ω = −1/3); then it tends to the DE dominated era (ω = −1). In GR, the cosmological constant can be considered as the simplest candidate for DE, but it suffers from two theoretical problems, coincidence and cosmological constant.[15] A number of models with DE to explain the late-time cosmic acceleration without the cosmological constant have been proposed (for more details of this topic, readers are advised to read review[16] and references therein).
Einstein proposed the idea of teleparallelism in a trail to unify gravity and electromagnetism into a unified field theory in 1928.[17] Teleparallel space–time is characterized by an affine connection whose curvature is vanishing, but has torsion. In the past two decades, the geometry of absolute parallelism (AP) has attracted the attention of many researchers in two directions. The first comprises the development of the geometry,[18,19] while the second focuses on the physical applications of this geometry.[20,21] The main reason for the name of teleparallel, which means “parallel at a distance”,[22] is that parallel transport of a vector depends on the path whose corresponding curvature is identically zero. It has been established that GR can, in fact, be re-constructed in teleparallel language.[23–29] The theory is known as the teleparallel equivalent of general relativity (TEGR). An interesting formulation of TEGR as a higher gauge theory can be found in Ref. [30]. To understand the acceleration of the universe, many theories of modified gravity have been introduced, among which is the attempt to generalize TEGR to f (T) theory similar to the idea of generalizing GR to f (R) gravity.[31–36]
For gravity theories which are invariant under both local Lorentz and diffeomorphism transformations, the tetrad and metric formulations are equivalent. The Lagrangian of TEGR is equivalent, up to a total divergence term, to the GR Lagrangian and thus the two theories are classically equivalent. Moreover, T, which is the scalar of the torsion, is local Lorentz invariant only up to a divergence. However, the f (T) theory is not local Lorentz invariant.[37]
Recently, many researchers have studied the Bianchi type I (BI) model in the presence of anisotropic DE. Rodrigues[38] constructed a BI ΛCDM cosmological model whose DE component preserves the non-dynamical character but yields an anisotropic vacuum pressure. Koivisto and Mota[39] proposed a different approach to resolve the CMB anisotropy problem; the earlier isotropy of the universe could be distorted by the direction-dependent acceleration of the later universe. Mota[40] investigated the BI cosmological model containing interacting DE fluid with non-dynamical anisotropic equation of state (EoS) and perfect fluid component. They suggested that if the EoS is anisotropic, the expansion rate of the universe becomes direction dependent at late time and the cosmological models with anisotropic EoS can explain some of the observed anomalies in CMB. The exact solution of BI is derived assuming some constraints on the coefficient of the second derivative of f (T).[41] This solution gives a constant torsion scalar. Here in this study, we apply the field equations of f (T) to the anisotropic homogenous model. Using the continuity equation, we derive a solution whose scalar torsion is constant.
It is the aim of the present study to apply the field equations of the f (T) gravitational theory to a tetrad field having homogeneity and anisotropy and try to solve some of the above mentioned problems that cannot be solved within the framework of GR. In Section 2, a brief review of the f (T) gravitational theory is presented. In Section 3, the tetrad field that has homogeneity and anisotropy is given and the application of the field equations of f (T) to this tetrad is done. The resulting differential equations are solved using two different methods in Section 4. In Section 5, we use two fluids and try to find a solution to f (T) and discuss some cosmological consequences. The final section is devoted to discussion.
The mathematical concept of the f (T) gravity theory is based on the Weitzenböck geometry. Our convention and nomenclature are as follows. The Latin indices describe the components of the tangent space to the manifold (spacetime), while the Greek ones describe the components of the spacetime. For a general spacetime metric, we write the line element as ds2 = gμ ν dxμ dxν = ηijeiμejν dxμdxν, where ηij = (−1, +1, +1, +1) is the Minkowski metric. eiμ is the covariant vector fields and its inverse eiμ is the contravariant vector fields, satisfying the orthogonality and unitary conditions eiμejμ = δij and eiμ eiν = δμν. In a spacetime with absolute parallelism, the parallel vector fields eiμ define the nonsymmetric affine connection[42] Γλμ ν = eiλ eiμ, ν, where eiμ, ν = ∂ν eiμ. The curvature tensor defined by the Weitzenböck connection, Γλμ ν, is identically vanishing. The torsion and the contortion components are defined as Tαμν = Γανμ − Γαμν = eaα (∂μeaν − ∂νeaμ) and Kμνα = − (Tμνα − Tνμα − Tαμν)/2.
The skew symmetric tensor Sμνρ has the form 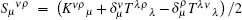

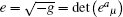
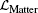

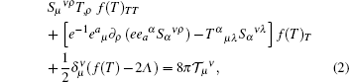
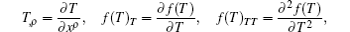
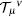
Now we are going to rewrite the field equations (
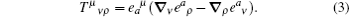
Using Eq. (
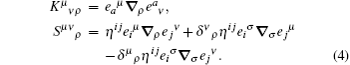
On the other hand, from the relation between the Weitzenböck connection and the Levi–Civita connection, one can write the Riemann tensor for the Levi–Civita connection, 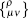
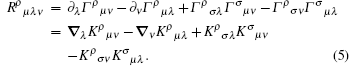
The associated Ricci tensor can then be written as
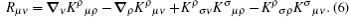
Now, by using the definition of the contorsion along with the relations K(μν) σ = Tμ (νσ) = Sμ (νσ) = 0 and considering that Sμρ μ = 2Kμρ μ = −Tμρμ, one has[46–52]
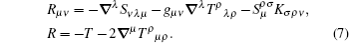
Equation (
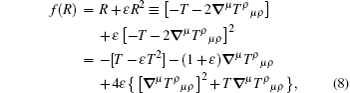
By using the equations listed above and after some algebraic manipulations, one can obtain


Equation (
The spatially homogeneous and anisotropic, Bianchi type I (BI), universe which has transverse direction x and two equivalent longitudinal directions y and z is given by[53]
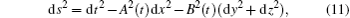

The dual of Eq. (

Using Eqs. (
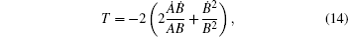
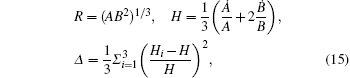
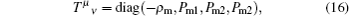

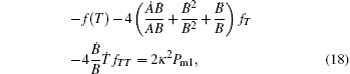

Equations (
Using Eqs. (
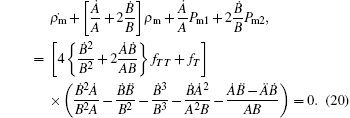
The second bracket contains two unknown functions A(t) and B(t), therefore, we need an extra condition to solve it. Here we will use two different procedures that have been used in the literature. Other conditions may give interesting results, which may be considered in future work.
For a spatial homogeneous metric, the normal congruence to homogeneous expansion implies that the expansion scalar θ is proportional to the shear scalar σ[54–62]


Using Eq. (
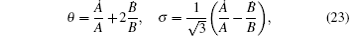
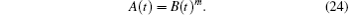
By using the above condition, the anisotropy parameter of the expansion is found to be
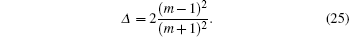
Equation (
By using Eq. (
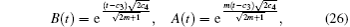



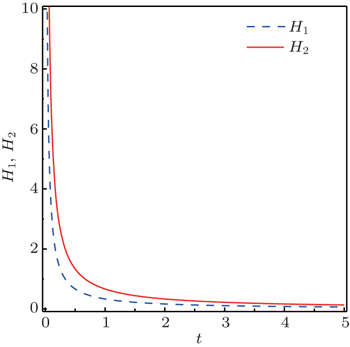
Recall the definition of the mean Hubble parameter mentioned in Eq. (
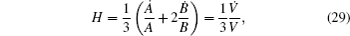
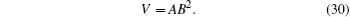
Using the following volumetric expansion law:[61]

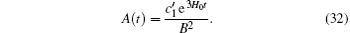
Equation (

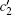

Following the same steps of the first procedure, we obtain
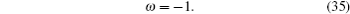
The density and the pressures of this model are also constants.
In the above two models, we have many problems: (i) constant scalar torsion which is responsible for making the energy density and the pressure constant, (ii) violation of conservation in spite of using Eq. (
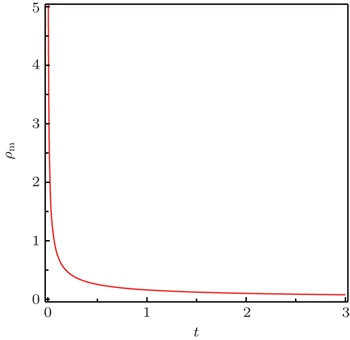
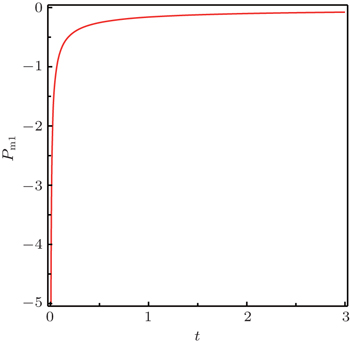
Here, we will use two equations of state, i.e., two fluids, and the relation between the scale factors given by Eq. (
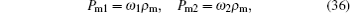
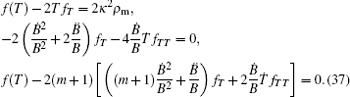
As f (T) in Bianchi type I spacetime is a function of time f(T → t), one easily can show that

Substituting Eq. (


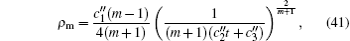
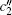

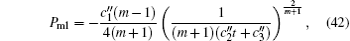

Using the relation between scale factors A(t) and B(t), i.e., Eq. (

So far, all the six unknowns are obtained.
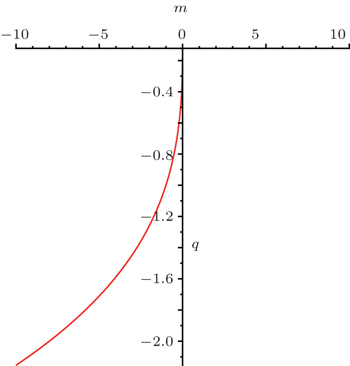
To see if the above model is consistent with the observations, i.e., it has an acceleration, we calculate the deceleration parameter and obtain

Equation (
In the present research, we have studied a spatially homogeneous and anisotropic BI universe. We use the continuity equation and write it as a product of two brackets. We assume the vanishing of the second bracket, which contains two unknown functions A(t) and B(t). To solve this bracket, we assume two different relations between these two unknown functions. First, we use the relation A(t) = B(t)m, where m ⩾ 2, and derive a solution for B(t) and consequently A(t). Second, we use the relation 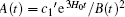
The most important property of the derived solutions of A(t) and B(t) is that the torsion scalar is a constant. The density and the pressures of these solutions are constants. We have calculated some cosmological parameters, such as the deceleration parameter. We show that our model is accelerating and its EoS parameter ω = −1. This means that f (T) in both cases can be regarded as a cosmological constant.[62] The above cosmological parameters show that the scale factors (
Another method has been considered using two different equations of state and a relation between the scale factors A(t) and B(t). This method enables us to derive the forms of f (T), A(t), B(t), ρm, Pm1, and Pm2 as in Eqs. (
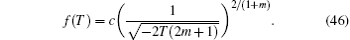
Note that we give f (T) in terms of the torsion scalar to explore f (T) in its usual form. But all the calculations in this work are performed using the time dependent form (
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 |