Cite this Article
Xu Chuang, Feng Feng, Li Ying-Jun. Path integral approach to electron scattering in classical electromagnetic potential. Chinese Physics B, 2016, 25(5): 050303  
Permissions
Path integral approach to electron scattering in classical electromagnetic potential
Xu Chuang†, , Feng Feng, Li Ying-Jun‡,
School of Science, China University of Mining and Technology, Beijing 100083, China

 

† Corresponding author. E-mail: xu.chuang.phy@gmail.com

‡ Corresponding author. E-mail: lyj@aphy.iphy.ac.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11374360, 11405266, and 11505285) and the National Basic Research Program of China (Grant No. 2013CBA01504).

Abstract
Abstract

As is known to all, the electron scattering in classical electromagnetic potential is one of the most widespread applications of quantum theory. Nevertheless, many discussions about electron scattering are based upon single-particle Schrodinger equation or Dirac equation in quantum mechanics rather than the method of quantum field theory. In this paper, by using the path integral approach of quantum field theory, we perturbatively evaluate the scattering amplitude up to the second order for the electron scattering by the classical electromagnetic potential. The results we derive are convenient to apply to all sorts of potential forms. Furthermore, by means of the obtained results, we give explicit calculations for the one-dimensional electric potential.

PACS: 03.65.–w;03.70. + k;
Keyword:electron scattering;path integral approach;quantum field theory;
1. Introduction

The original concept of the path integral approach may stem from the Wiener integral, which was proposed by Norbert Wiener in order to study the stochastic process of Brownian motion. In 1933, Dirac[1] extended Wiener’s idea to bring in quantum mechanics for establishing the action principle and its Lagrangian formalism.

The thorough and complete path integral approach was developed by Richard Feynman[2] in 1948. In 1963, Feynman expressed the gravitational interaction of two particles by means of an interchange of a virtual graviton.[3] The mathematical technique of the path integral approach was first applied to non-Abelian gauge fields. In 1967, Faddeev and Popov[4] utilized the path integral approach to obtain the detailed quantization rules which are observed to calculate the contribution from arbitrary Feynman diagrams in the theory of SU(2) gauge invariant fields. In 1971, with the help of the path integral approach and dimensional regularization method, Hooft[5] successfully demonstrated that massive Lagrangians for non-Abelian gauge theories without anomalies are renormalizable. At present, the Higgs boson,[6–9] which is the last elementary particle with a mass near 125 GeV predicted by the standard model of particle physics, had been discovered in the ATLAS and CMS experiments at CERN’s Large Hadron Collider on 4 July 2012, and all observational evidence points to the fact that quantum field theory provides an accurate description of all known elementary particles. In retrospect, it is clearly shown that the path integral approach is of great significance for the development of quantum field theory.

On the other hand, since the first ruby laser was invented in 1960 by Maiman at Hughes Laboratories, particularly with the rapid development of chirped pulse amplification, laser power has achieved tremendous growth. Nowadays, it has been reported that the present world highest laser intensity is the HERCULES laser produced by the University of Michigan, whose focused laser intensity has achieved as high as 2 × 1022 W/cm2.[10] Consequently, a large number of theoretical and experimental phenomena which are involved in the processes of the electron scattering in the strong laser field, such as acceleration of electrons,[11,12] Thomson backscattering of optical laser light off relativistic electrons,[13–16] and nonlinear Compton scattering,[17–21] need to be discussed further.

Therefore, seeing that many new operator methods have witnessed a boom in quantum mechanics, such as the operator-Hermite-polynomial method,[22] as far as the application of the method is concerned, we believe that it is crucial to treat the classical problem of the electron scattering with the path integral approach which plays a central role in quantum field theory. The main merit of the path integral approach is that it provides a comparatively convenient road to quantization and to expression for correlation function, which is closely related to amplitudes for electron scattering processes.

This paper is organized as follows. In Section 2, we introduce the Grassmann algebra, generating functional and correlation functions in the path integral approach of quantum field theory. In Section 3, we apply the perturbation technique to calculate the correlation function up to the second order. Based on Lehmann–Symanzik–Zimmermann (LSZ) reduction formula, we derive a general result for the electron scattering off the classical electromagnetic potential. In Section 4, we shall present an explicit calculation that is the electron scattering off the one-dimensional time-independent electric potential to illustrate the use of the results presented in Section 3. In Section 5, we shall discuss a heuristic application of the Gaussian barrier. Finally, in Section 6, we shall give a brief summary.

2. Path integral treatment

The foundational component of path integral formalism is the generating functional of correlation functions.[23] For the spinor field, it reads

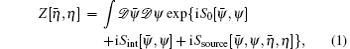
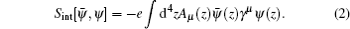
where S0, Sint, and Ssource are free action, interactional action, and source action, respectively, ψ and η are Grassmann fields whose values are anticommuting numbers. For the purpose of describing the interaction of spinor field and electromagnetic field, we choose as

To begin, we need to refer to the definition of the functional derivatives, δ/δη and , as follows. With respect to a four-dimensional case, the functional derivatives obey the conditions

and

In addition, if η and are Grassmann numbers, they satisfy

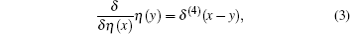
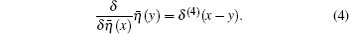
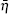
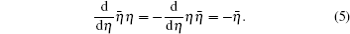
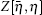
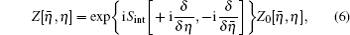
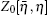
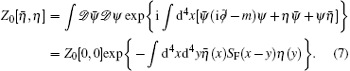
To evaluate the path integral more generally, we must split up the exponential into the interaction and free term including source. Meanwhile, to fix the problem, we can use a trick that replaces the fields and ψ in the interaction part by functional derivatives. It would be nice if we can pull the interaction part out of the integral and perform the remaining integral. Then, equation (1) becomes

where is the generating functional of the free spinor field

Notice that Z0[0,0] actually is the Gaussian integral and can be performed precisely. So as to simplify the subsequent calculations, we will drop it directly. Therefore, we redefine it as

where SF(x − y) is called the Feynman propagator for the spinor field. In position space, it is written as

On the basis of path integral formulism, the two-point correlation function for the spinor field is given by

where |Ω⟩ denotes the vacuum state of interacting theory, T is called time-ordered product, which instructs us to place the operators that follow in order with the latest to the left. The subscript H means working in the Heisenberg picture.

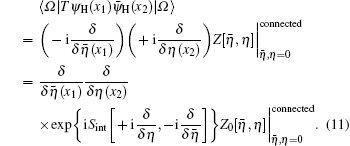
Consider Eq. (10), in fact, the disconnected diagrams in the numerator can be just canceled by the denominator, only the connected diagrams can make contributions to the correlation function. In other words, for the two-point correlation function, we can simply sum all connected diagrams with two external points. Now it reads

3. Perturbative expansion for the generating functional

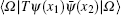
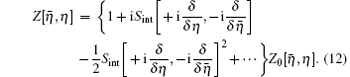
To compute , we would like to expand the generating functional perturbatively with respect to the powers of Sint,

The zero-order term in the expansion of Eq. (11) is given by

It is nothing but the Feynman propagator.

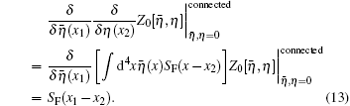
For the first-order term, it reads

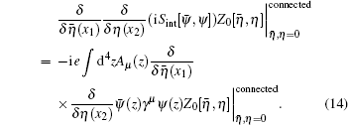
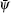
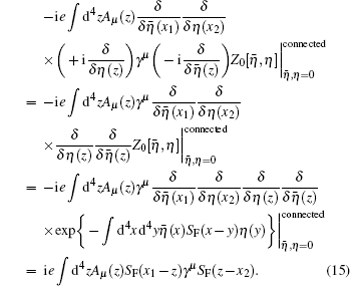
We replace the fields and ψ with functional derivatives. Thus, equation (14) becomes

For the second-order term, it becomes complicated. We need to calculate the following quantity:

Repeat using the above trick, i.e., replace the fields and ψ by functional derivatives. Thus, equation (16) becomes

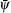
By applying the generalized LSZ reduction formula[24] for the spinor field, we establish the connection between the two-point correlation function and the S matrix. Namely, we have

where u is the spinor wave function of the electron, ū is the Dirac conjugation of u, and the quantity Z that appears in this equation is a c number, known as field-strength renormalization factor. Since we only work up to the second-order term, we set Z = 1.

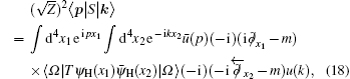
To isolate the interaction part of the S matrix, we define the T matrix as

It is easy to see that, for the identity matrix, it indubitably links the zero-order term which is trivial.

The lowest non-trivial order contribution for T matrix is the first-order term. Hence, combine the result of Eq. (15), the only thing we need to do is to calculate the quantity

Substituting the above result into Eq. (18), we have

where Ãμ(p − k) is the four-dimensional Fourier transform of Aμ(z),

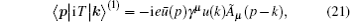
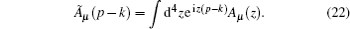
Continuing to consider the situation of the second-order term, we obtain

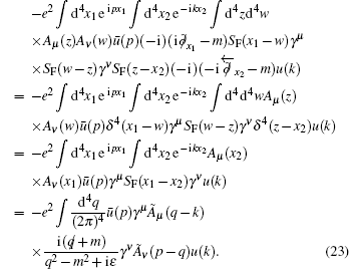
Substituting the result of Eq. (23) into Eq. (19), we have

where S̃F(q) is the Feynman propagator in momentum space, it has the form

Therefore, summing up the above, we finally have

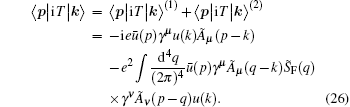
So far, we have derived the amplitude of electron scattering up to the second order which is completely general, it can be used to calculate electron scattering with arbitrary form of electromagnetic potential.

4. Explicit calculation for the one-dimensional case

In this section, we have now shown that we utilize the result obtained in Eq. (26) to apply to a simple case of one-dimensional classical electric potential scattering. For the sake of simplicity, we shall suppose that the electron travels along the positive z3 axis, then let us set

where , , k3 and p3 are the initial and final momentum of electron, respectively. Meanwhile, we set k3 > 0. Then, at the level of the first order, the T-matrix element becomes

In the last line, we define V(z3) = eA0(z3).

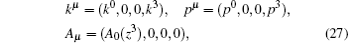
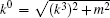
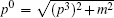
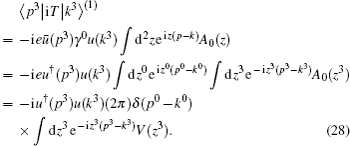
To describe the electron scattering process completely, we have to integrate over the final momentum p3 with the Lorentz-invariant measure,

In order to make our subsequent calculations easily, it is convenient to write the normalization condition for spinor u(p) as

and

where ξs is a two-component constant spinor and s is the spinor index.

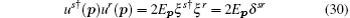
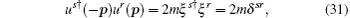
With the aim of performing the integration over p3, we use the identity equation[25] as

Then, equation (29) will be split into two separate parts.

Namely, for the reflection part of electron scattering, p3 = −k3, at the level of first order, we have

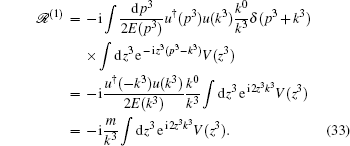
Analogously, for the transmission part, p3 = k3, we have

At the level of second order, the T-matrix element has

Here, to complete the integral over q3, we draw support from the method of residue theorem and choose the contour satisfying the Feynman prescription to deal with it. Namely, when w3 > z3 we can perform the q3 integral by closing the contour below the axis. When w3 < z3 we close the contour above the axis. Then, equation (35) becomes

where the function ϒ(w3, z3; p0, p3) is defined as

Similarly, we have to implement the integral over p3, again, by using Eq. (32), for reflection, p3 = −k3, at the level of second order, we obtain

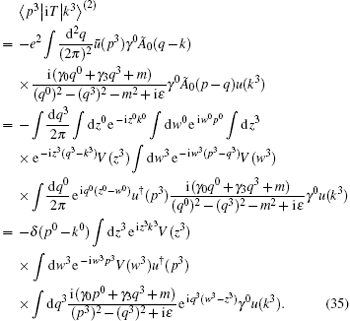
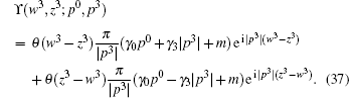
For transmission, p3 = k3. At the level of second order, we obtain that

5. Application in analyzing Gaussian barrier

As a kind of concrete application, we choose V(z3) as the Gaussian barrier given that it has a bearing on the strong laser field in optics, which is a radially symmetrical distribution whose potential variation is given by

where V and α are constant real numbers, and V > 0, α > 0. Meanwhile, we assume that the magnitude of momentum of incident electron satisfies the condition k3 ≪ α, because experimentally the initial velocity of incident electron is typically small.

For convenience, much emphasis is placed on the transmission part. Our calculations presented in Section 4 show that equations (34) and (39) are able to give a clear physical picture for scattering by the Gaussian barrier on condition that the approximation up to the second order is accurate enough. Straightforwardly, we have

and

Notice that in the second line from the bottom of Eq. (42), we take an approximation that is

under the condition of k3 ≪ α.

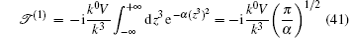
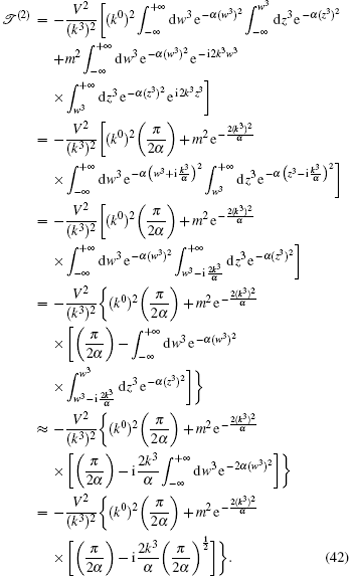
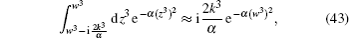
Then, the total transmission amplitude including the trivial part of the zero order is given as follows:

6. Summary

In the previous five sections, by using path integral approach, we have calculated the first- and second-order contributions of quantum field theory to the process of the electron scattering. Indeed, according to the general principle of quantum field theory, we need to quantize the spinor field and electromagnetic field simultaneously. However, to compare our final results directly with those of the single-particle Schrodinger equation or Dirac equation, we no longer quantize the electromagnetic field. Instead, we treat the field as a given, classical four-dimensional potential Aμ (x) throughout.

Usually, it is sufficient to solve most scattering problems using single-particle theory. Yet, sometimes one needs to consider more complicated situations which should use field theory like scattering problems in the strong laser fields. Therefore, the purpose of this paper is to show that the expression we derive in Eq. (26) is able to give a map describing the phenomena that contain kinds of scattering problems between quantum field theory and quantum mechanics. Moreover, we note that the path integral treatment of the one-dimensional electron scattering in classical electric potential may be related to give a possible explanation of the Klein paradox.[26–32]

Reference
1Dirac P A M1933Physik. Zeits. Sowjetunion364
2Feynman R P 1948 Rev. Mod. Phys. 20 367
3Feynman R P1963Acta Phys. Pol.24697
4Faddeev L DPopov V N 1967 Phys. Lett. 25 29
5Hooft G’t 1971 Nucl. Phys. 35 167
6Englert FBrout R 1964 Phys. Rev. Lett. 13 321
7Higgs P W 1964 Phys. Rev. Lett. 13 508
8Higgs P W 1966 Phys. Rev. 145 1156
9Weinberg S 1976 Phys. Rev. Lett. 36 294
10Yanovsky VChvykov VKalinchenko GRousseau PPlanchon TMatsuoka TMaksimchuk ANees JCheriaux GMourou GKrushelnick K 2008 Opt. Express 16 2109
11Faure JGlinec YPukhov AKiselev SGordienko SLefebvre ERousseau J PBurgy FMalka V 2004 Nature 431 541
12Faure JRechatin CNorlin ALifschitz AGlinec YMalka V 2006 Nature 444 737
13Schoenlein R WLeemans W PChin A HVolfbeyn PGlover T EBalling PZolotorev MKim K JChattopadhyay SShank C V 1996 Science 274 236
14Tomassini PGiulietti AGiulietti DGizzi L A 2005 Appl. Phys. 80 419
15Schwoerer HLiesfeld BSchlenvoigt H PAmthor K USauerbrey R 2006 Phys. Rev. Lett. 96 014802
16Jochmann AIrman ABussmann MCouperus J PCowan T EDebus A DKuntzsch MLedingham K W DLehnert USauerbrey RSchlenvoigt H PSeipt DStohlker ThThorn D BTrotsenko SWagner ASchramm U 2013 Phys. Rev. Lett. 111 114803
17Hartemann F VKerman A K 1996 Phys. Rev. Lett. 76 624
18Bula CMcDonald K TPrebys E JBamber CBoege SKotseroglou TMelissinos A CMeyerhofer D DRagg WBurke D LField R CHorton-Smith GOdian A CSpencer J EWalz DBerridge S CBugg W MShmakov KWeidemann A W 1996 Phys. Rev. Lett. 76 3116
19Boca MFlorescu V 2009 Phys. Rev. 80 053403
20Seipt DKampfer B 2011 Phys. Rev. 83 022101
21Liang G HLü Q ZTeng A PLi Y J 2014 Chin. Phys. 23 054103
22Fan H YZhang P FWang Z 2015 Chin. Phys. 24 050303
23Peskin M ESchroeder D V1995An Introduction to Quantum Field TheoryWestview Press10.1063/1.2807734
24Lehmann HSymanzik KZimmermann W 1955 Nuovo Cimento 1 205
25Leo S DRotelli P 2009 Eur. Phys. J. 62 793
26Klein O 1929 Z. Phys. 53 157
27Nikishov A I 1970 Nucl. Phys. 21 346
28Hansen ARavndal F 1981 Phys. Scr. 23 1033
29McKellar B H JStephenson G J 1987 Phys. Rev. 36 2566
30Manogue C A 1988 Ann. Phys. 181 261
31Dombey NCalogeracos A 1999 Phys. Rep. 315 41
32Katsnelson M INovoselov K SGeim A K 2006 Nat. Phys. 2 620