Dynamics of cubic–quintic nonlinear Schrödinger equation with different parameters
Numerical solutions of the cubic–quintic NSE by symplectic method with
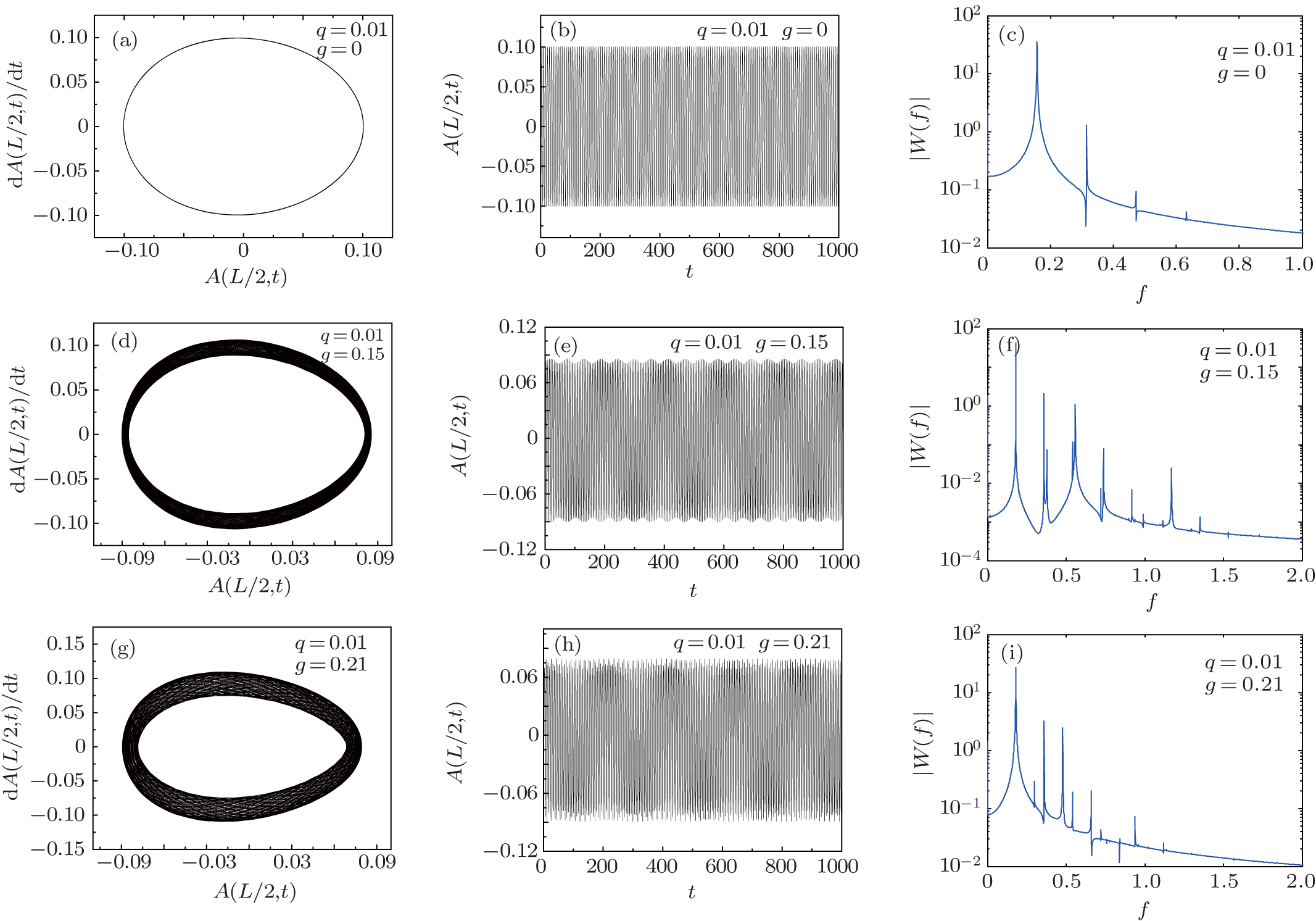
Dynamics of cubic–quintic nonlinear Schrödinger equation with different parameters |
Numerical solutions of the cubic–quintic NSE by symplectic method with |
 |