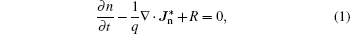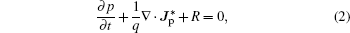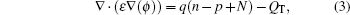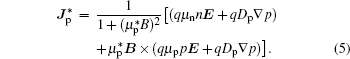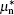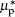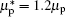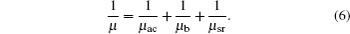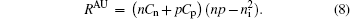Numerical simulation of the magnetoresistance effect controlled by electric field in p–n junction
Institute of Microelectronics, School of Physical Science and Technology, Lanzhou University, Lanzhou 730000, China
† Corresponding author. E-mail: yangjh@lzu.edu.cn
1. IntroductionIn view of the physical interest and potential applications, magnetoresistance (MR) effects have attracted a lot of theoretical and experimental attention. MR effects can be achieved by using non-magnetic materials such as doped silicon,[1] GaAs,[2] and magnetic materials.[3,4] However, compared with magnetic material, non-magnetic material has a large MR ratio and the resistivity increases approximately linearly with the external magnetic field, which makes the non-magnetic material more attractive to random access memory, ultrasensitive magnetic field sensors,[5] logic devices,[6,7] etc. By virtue of long spin coherence[8,9] and compatibility with the current CMOS technology, silicon is a promising material for investigating the magnetoresistance effect.
Many researches based on doped silicon have been carried out to explore the effect. Michael et al. have reported that the large positive magnetoresistance effect can be induced by breaking the quasi-neutrality of the space-charge effect.[10] While another mechanism was also proposed, i.e., the magnetoresistive effect can be achieved by shrinking the acceptor wave functions in the direction perpendicular to the magnetic field.[11] Meanwhile, it can also be achieved by the process of impact ionization[12] which is controlled by magnetic field.
However, a few methods are put forward to regulate MR when the magnetic field is fixed. Though varying the geometrical size[13] can achieve it, it is inconvenient for practical applications. In the present work, the magnetoresistance effect of the p–n junction induced by the space-charge effect under an electric field is studied by simulation. The results show that a wide range of magnetoresistance can be controlled, which implies that it is a more potential method to adjust magnetoresistance by using the electric field which is introduced by gate voltage.
2. Theoretical method and formulasClassical p–n theories proposed by Shockley[14] are basic to analyse the properties of the p–n junction. This theory consists of a set of fundamental equations, which need to be modified slightly when they are used to simulate the properties of p–n under the external magnetic field and electric field.
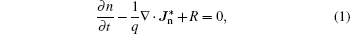
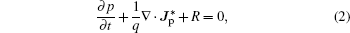
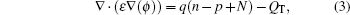

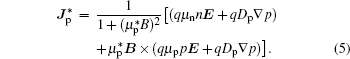
Equations (1) and (2) are the continuity equations of current for electron and hole. Here, n and p are the electron and hole density respectively, R represents the net recombination rate (including the Shockley–Read–Hall recombination rate and Auger recombination rate), and q denotes the elementary charge. Equation (3) is the electrostatic equation which is also known as the Poisson equation, whereas the permittivity, φ is the electric potential and N is the ionized net doping concentration, QT represents the charge due to traps and defects with setting QT to be zero). Equations (4) and (5) give the electron and the hole current density, which are modified when the magnetic field is perpendicular to the current densities,[15] here, μn and μp are the electron and hole drift mobility, 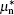 and
and 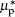 are the electron and hole Hall mobility, which are assumed to be proportional to the drift mobility[16] (
are the electron and hole Hall mobility, which are assumed to be proportional to the drift mobility[16] ( , and
, and 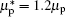 ), and Dn and Dp denote the electron and hole diffusion coefficient.
), and Dn and Dp denote the electron and hole diffusion coefficient.
To obtain accurate results, the Lombardi CVT Model,[17] which contains the effect of a transverse field, doping- and temperature-dependent carrier mobility, is used. In this model, the mobility is given by three components that are composed according to the Matthiessen rule:
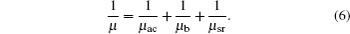
On the right-hand side of Eq. (5), the first component μac is the mobility limited by surface phonon scattering, and μb is the mobility determined by both doping concentration and temperature. The final component μsr takes into account the surface roughness scattering. More details are shown in Ref. [17].
For numerical simulation of a semiconductor device, the carrier generation-recombination is the crucial process that must be considered. In this paper, Shockley–Read–Hall recombination[18] and Auger recombination[19] within the bulk of the semiconductor are adopted.

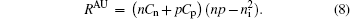
Here,
Ei and
Et give the intrinsic Fermi level and trap energy level respectively. For simplicity, we assume that the energy level of trap centers overlaps with the intrinsic Fermi level.
τn and
τp are the electron and hole lifetime, respectively. Owing to the fact that electron and hole may recombine or be generated at interfaces,
τn and
τp need to be modified
[20] when Shockley–Read–Hall recombination is used at interfaces. Equation (
8) gives the Auger recombination rate. In Eq. (
8),
Cn and
Cp are Auger coefficients for electron and hole,
ni is the intrinsic carrier concentration given by Boltzmann statistics,
n and
p are the electron and hole densities, which can be given by the Boltzmann approximation.
During numerical simulation, several boundary conditions (ohmic contacts, insulated contacts, Neumann boundaries) must be considered. To implement ohmic contacts, Dirichlet boundary conditions, where surface potential, electron concentration and hole concentrations are fixed, are taken into account. In the oxide region, the zero normal current condition Jn · s = Jp · s = 0) is imposed.[16] To ensure that the current only flows out of the p–n junction through the contact, Neumann boundaries are adopted.
To discretize those equations, the finite-difference method and the box integration method are used in order to solve them in an appropriate mesh. After discretization, the Newton iteration is used to solve the partial differential equations. The SGFramework,[21] a highly flexible partial differential equations solver, is introduced.
The structure simulated is shown in Fig. 1. Aluminum film is used to form an Ohmic contact. In order to implement a controllable electric field, SiO2 film is formed above the p–n junction surface and then an electrode gate is formed in sequence (shown in Fig. 1). It is convenient to analyze the effect of an abrupt p–n junction with uniform doping under an electric field and magnetic field at room temperature. The simulation parameters are shown in Table 1.
Table 1.
Table 1.
 Table 1. Simulation parameters. .
| Parameter |
Value |
| Temperature (T) |
300 K |
| Dielectric constant (ɛSi) |
11.8 |
| Dielectric constant (ɛSiO2) |
3.9 |
| Acceptor concentration (NA) |
1014 cm−3 |
| Donor concentration (ND) |
1014 cm−3 |
| SiO2 thickness (d) |
0.1 μm |
| Table 1. Simulation parameters. . |
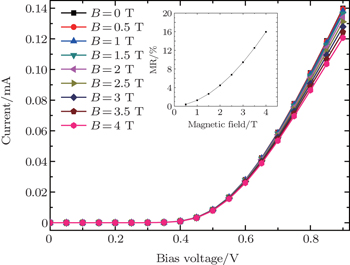
3. Numerical results and discussionFigure 2 shows the I–V characteristics of the p–n junction at T = 300 K for various magnetic fields. Curent is gradually suppressed with increasing magnetic field due to the drastic change of the space-charge region. In order to describe the variation of current with applied magnetic field, here the magnetoresistance (MR) ratio is defined as MR(%) = [R(B) − R(0)]/R(0) × 100%, where R(0) and R(B) are the resistance (V/I) at zero and applied magnetic field. The inset in Fig. 2 shows the MR curve at Vbias = 0.9 V. It is fitted well with the parabolic relation (MR ∝ (μB)2), which is similar to the results reported in Ref. [13].
Figure 3(a) demonstrates the space-charge regions of p-type silicon and n-type silicon. Its spatial distribution of electric field is homogeneous. However, when an external magnetic field is applied, the homogeneous distribution is broken. As indicated in Fig. 3(b), when a positive magnetic field is applied, holes and electrons are attracted to the surface of the sample by the Lorenz force and accumulate. The spatial distribution and width of the space-charge region change. It is analogical to the scenario of applying a negative magnetic field.
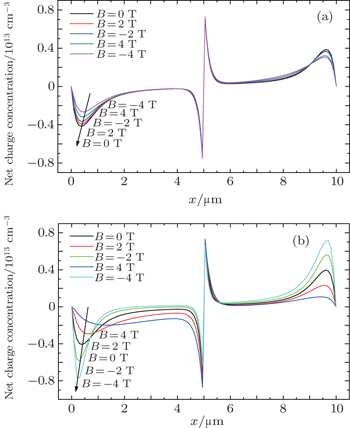
Figures 4(a) and 4(b) display the net charge concentrations of the space-charge region at y = 2.5 μm and y = 0.3 μm. As illustrated, there is no apparent distinction from the distribution of net charge concentration at y = 2.5 μm for different magnetic fields, however, a dramatic change appears at y = 0.3 μm (the difference between the distribution of net charge concentration at x = 0 μm and that at x = 10 μm is induced by the carriers injected). The width of the space-charge region far from the gate (y = 0.3 μm), compared with that under the condition without magnetic fields, increases but near the gate region decreases when we apply a positive magnetic field, the shape of the space-charge region changes from rectangular to trapezoid (Fig. 3(b)), which is well matched to the result reported by Wan et al.[13] Moreover, it is clearly observed that the net charge concentration changes drastically in the p-type but slightly in the n-type. It can be considered to be due to the different properties about hole and electron, which leads to various performances of magnetic field.
In order to discuss the magnetoresistance effect of the p–n junction under an electric field clearly, here, the MR ratio is modified into M1(%) = [R(B,Vgate) − R(0)]/R(0) × 100%, where R(0) and R(B,Vgate) are the resistance (V/I) at zero applied magnetic field and that at applied magnetic field B and gate voltage Vgate. MR1 can also be given by MR1 = MR + ΔRE/R0 + f (B,E), where ΔRE = R(B = 0 T,Vgate) − R(B = 0 T,Vgate = 0 V) is the resistance variation (B = 0 T). MR and ΔRE/R0 are the resistance variation ratios without gate voltage and without magnetic field respectively, f (B,E) is an interaction term induced by the interaction between magnetic field and gate voltage.
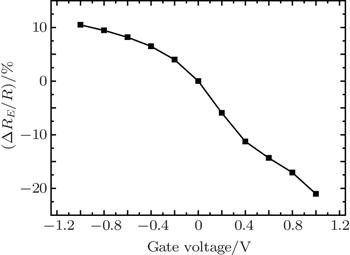
At the zero-magnetic field, the resistance increases with an increase of negative gate voltage applied and decreases with the increase of positive gate voltage. The resistance variation ratio (ΔRE/R0) without magnetic field is shown in Fig. 5. As indicated, ΔRE/R0 increases and gradually tends to be saturated with negative gate voltage decreasing. When positive gate voltage is applied, ΔRE/R0 decreases linearly with gate voltage increasing, which can be seen from the fact that the ability for ΔRE/R0 to compensate for MR1 is enhanced. The change contributes to the difference in electrical property (μn > μp) and the variation of hole and electron concentration. When positive voltage is applied to the gate, the electron concentration increases and the hole concentration decreases, resulting in the electron current increasing and the hole current decreasing. Whereas the increase of electron current dominates the decrease of hole current because of μn > μp, thus the total current increases, which indicates the decrease of resistance. It is opposite to the scenario of applying negative gate voltage.
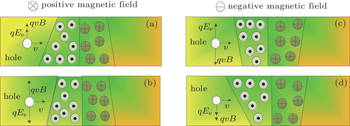
To explore the variation of f (B,E), the force analysis of hole under magnetic field and gate voltage is shown in Fig. 6. (The electron is not shown because a slight change occurs in the n-type. The colour has no special implication.) As displayed, when condition (a) (Fig. 6(a)) and condition (d) (Fig. 6(d)) are imposed on the device, the Lorentz force and electric field force =both contribute to the spatial variation of hole concentration and electric field inhomogeneity of the space-charge region in the p-type region, whereas carriers move toward the same orientation, resulting in carrier scattering aggravating, leading to f (B,E) < 0 (compensating for MR). However, for the conditions (b) and (c), the Lorentz force and electric field force compete with each other, the f (B,E) depends on the stronger of the two forces. When electric field force qEe dominates Lorentz force qvB, the compensating effect occurs.
On the basis of the above discussion, the results shown in Fig. 7 can be easily understood. As shown in Fig. 7, at a low magnetic field without gate voltage (ΔRE/R0 = f (B,E) = 0), MR1 shows an approximately quadratic relationship and is symmetrical about B = 0 T. Whereas with the absolute value of gate voltage increasing, the symmetry of MR1 curves is gradually broken because of f (B,E) ≠ 0. It demonstrates that MR is dependent on the polarity of magnetic field, which is different from other results.[10–13]
In addition, it can also be noted that the MR is about 0.396% with a magnetic field of 0.5 T and an applied bias voltage of 0.9 V, while an 11.107% magnetoresistance ratio is achieved with a negative gate voltage of −1 V at the same bias voltage. The MR is enlarged substantially due to the contribution of ΔRE/R0 (f (B,E) is small.) However, the distinction of the magnetoresistance curve between various negative gate voltages disappears with magnetic field increasing and gate voltage decreasing. It can be explained by the fact that the ΔRE/R0 tends to be saturated which is shown in Fig. 5. For a positive gate voltage, the magnetoresistance ratio can reach −1.740% when 0.2 V is applied to the gate with B = 2 T for a bias of 0.9 V, but the magnetoresistance ratio reaches 4.477% when only magnetic field B = 2 T is applied. The difference is induced by the compensating of ΔRE/R0 and f (B,E) for magnetoresistance, which makes the magnetoresistance reduced. While f (B,E) becomes more important with positive gate voltage increasing, which can be seen from the degree of symmetry breaking.
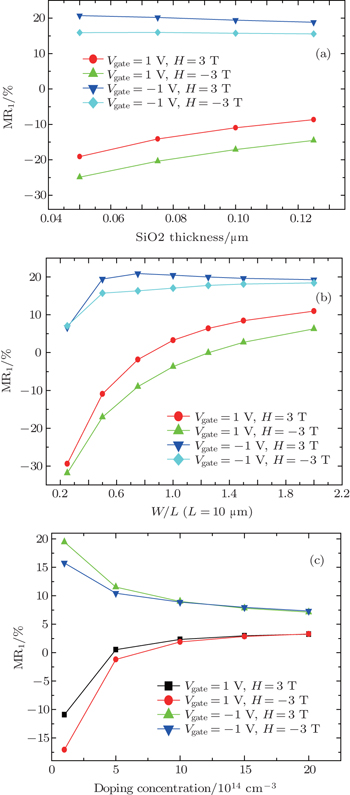
Figure 8 shows variations of magnetoresistance with SiO2 thickness, W/L and doping concentration respectively. As indicated in Fig. 8(a), with SiO2 thickness increasing, magnetoresistance increases linearly because of the compensation capabilities of ΔRE/R0 reducing when positive gate voltage is applied and decreases slightly with applied negative voltage increasing due to ΔRE/R0 reducing. On account of f (B,E) ≠ 0, the intervals of MR1 curves occur when different polar magnetic fields are applied at the same gate voltage. Figure 8(b) displays the variations of magnetoresistance with W/L for different values of Vgate and B. The magnetoresistance tends to be saturated with W/L increasing. It derives from MR tending to saturation[10] and ΔRE/R0 gradually decreasing to zero due to the fact that the electric field diminishes with W increasing. The variations of magnetoresistance with doping concentration are shown in Fig. 8(c). There is some evidence that magnetoresistance would be saturated at high doping concentration. The carrier scattering aggravating is the significant mechanism, which makes MR and f (B,E) gradually decrease to zero.
4. ConclusionsIn this paper, the magnetoresistance effect of the p–n junction under an electric field at room temperature is simulated. The results indicate that it is a useful method to control magnetoresistance by gate voltage. A larger MR can be achieved by negative gate voltage, and it can also be compensated by positive gate voltage. Meanwhile, MR is dependent on the polarity of magnetic field when gate voltage is applied. Furthermore, the doping concentration, SiO2 thickness and p–n junction size are also investigated. The results will promote the applications of silicon-based magnetoresistance devices such as a reconfigurable logic device based on magnetoresistance, access memories, and so on.