Cite this Article
Li Jin-Yuan, Fang Nian-Qiao, Zhang Ji, Xue Yu-Long, Wang Xue-Mu, Yuan Xiao-Bo. (2+1)-dimensional dissipation nonlinear Schrödinger equation for envelope Rossby solitary waves and chirp effect. Chinese Physics B, 2016, 25(4): 040202  
Permissions
(2+1)-dimensional dissipation nonlinear Schrödinger equation for envelope Rossby solitary waves and chirp effect
Li Jin-Yuan1, 2, 3, †, , Fang Nian-Qiao1, Zhang Ji2, 3, Xue Yu-Long4, Wang Xue-Mu4, Yuan Xiao-Bo1
School of Ocean Sciences, China University of Geosciences (Beijing), Beijing 100083, China
Marine Geology and Hydrology Research Laboratory, Guodian New Energy Technology Research Institute, Beijing 102209, China
Zhong Neng Power-Tech Development Company Limited, Beijing 100034, China
Marine Geological Institute of Hainan Province, Haikou 570206, China

 

† Corresponding author. E-mail: lijinyuan198007@sina.com

Project supported by the National Natural Science Foundation of China (Grant No. 41406018).

Abstract
Abstract

In the past few decades, the (1+1)-dimensional nonlinear Schrödinger (NLS) equation had been derived for envelope Rossby solitary waves in a line by employing the perturbation expansion method. But, with the development of theory, we note that the (1+1)-dimensional model cannot reflect the evolution of envelope Rossby solitary waves in a plane. In this paper, by constructing a new (2+1)-dimensional multiscale transform, we derive the (2+1)-dimensional dissipation nonlinear Schrödinger equation (DNLS) to describe envelope Rossby solitary waves under the influence of dissipation which propagate in a plane. Especially, the previous researches about envelope Rossby solitary waves were established in the zonal area and could not be applied directly to the spherical earth, while we adopt the plane polar coordinate and overcome the problem. By theoretical analyses, the conservation laws of (2+1)-dimensional envelope Rossby solitary waves as well as their variation under the influence of dissipation are studied. Finally, the one-soliton and two-soliton solutions of the (2+1)-dimensional NLS equation are obtained with the Hirota method. Based on these solutions, by virtue of the chirp concept from fiber soliton communication, the chirp effect of envelope Rossby solitary waves is discussed, and the related impact factors of the chirp effect are given.

PACS: 02.30.Jr;47.35.Fg;92.10.Hm;
Keyword:(2+1)-dimensional dissipation nonlinear Schrödinger equation;envelope Rossby solitary waves;chirp effect;two-soliton solutions;
1. Introduction

It is generally known that the ocean and atmosphere move endlessly in complex patterns and on diverse scales. To discuss the whole dynamics of this enormous spectrum of motions is almost impossible. So our special interest is the so-called large scale motions which are prominently affected by the rotation effect of the earth. Among these large scale motions, the nonlinear Rossby waves have attracted considerable attention from the oceanic and atmospheric field in recent years. Long[1] first found the Rossby solitary waves in the westerly shear flow in the 1960s, then Benney,[2] Redekopp[3] and other investigators pushed the research forward. In the 1970s∼1980s, driven by blocking dynamics, the nonlinear theory of Rossby solitary waves achieved rapid development and formed the solitary waves theory, dipole waves theory, and envelope solitary waves theory. For the Rossby solitary waves, some weakly nonlinear models for the evolution of Rossby solitary waves have been extensively studied in the past. Among these, the Korteweg–de Vries (KdV) equation,[4–6] modified KdV equation,[7,8] and Boussinesq equation[9] were derived to describe the classical Rossby solitary waves; the Benjamin–Ono equation[10,11] was obtained to show the algebraic Rossby solitary waves with non-uniform horizontal shear of zonal flow in infinite depth fluid, while the Intermediate Long Wave equation[12,13] was used to describe the condition in finite depth fluid. For the envelope Rossby solitary waves, the nonlinear Schrödinger (NLS) equation was first obtained by Benney[14] and Yamagata,[15] respectively. Later, Luo[16] also derived the NLS equation to express the envelope Rossby solitary waves and showed that the atmospheric blocking in the mid-high latitudes could be explained better by employing a dipole envelope Rossby solitary wave. With the development of theory, the higher order NLS equation[17] was derived to describe the dynamic behavior of envelope Rossby solitary waves. However, all the above-mentioned models are (1+1)-dimensional and used to describe the propagation of Rossby solitary waves or envelope Rossby solitary waves in a line, which are not enough to reflect the evolution of Rossby solitary waves in the real ocean and atmosphere. It seems that few previous researches involved the problem. The purpose of this paper is to obtain a new (2+1)-dimensional dissipation nonlinear Schrödinger equation (DNLS), which is more suitable to describe the evolution of envelope Rossby solitary waves in the real ocean and atmosphere. Especially, due to the dissipation character of the real oceanic and atmospheric motion, we will embed the dissipation effect in the study.

On the other hand, in the fiber soliton communication field, the chirp effect is proposed to express frequency modulation in the process of transmission. The interaction of the nonlinear and dispersive effect can cause the excursion of the center wave and lead to chirp effect. Drawing lessons from the chirp concept in fiber soliton communication, Song[18] investigated the chirp effect of an internal wave, while we will discuss the chirp effect during the propagation of envelope Rossby solitary waves.

Besides the above-mentioned problems, we shall use these methods to solve the soliton equations, such as the first integral method,[19] similarity transformation,[20] Jacobi elliptic function expansion method,[21] Bäcklund transformation method,[22] Darboux transformation method,[23] and so on. In the paper, we will derive the one-soliton and two-soliton solutions of the (2+1)-dimensional NLS equation by employing the Hirota method[24] and analyze the chirp effect based on the analytical solutions.

This paper is organized as follows. In Section 2, from the rotational potential vorticity-conserved equation with dissipation, by constructing a (2+1)-dimensional stretching transformation of time and space, a (2+1)-dimensional DNLS equation is derived, which is a generalization of the (1+1)-dimensional NLS equation obtained by the former. In Section 3, by theoretical analyses, the character of the (2+1)-dimensional envelope Rossby solitary waves under the influence of dissipation is studied. Section 4 will be devoted to investigating the one-soliton and two-soliton solutions of the DNLS equation by using the Hirota method and dissipation effect. Based on these analytical solutions, the chirp effect of envelope Rossby solitary waves will be discussed in Section 5. Some conclusions are given in the last section.

2. Derivation of the (2+1)-dimensional DNLS equation

The basic equation of motion used in previous studies is the following non-dimensional quasi-geostrophic equation in the form of potential-vorticity:

But we note that a disadvantage exists for Eq. (1): envelope Rossby solitary waves are established in the zonal area, and cannot be applied directly to the spherical case; we need to consider envelope Rossby solitary waves in rotational fluid. So let us take the plane polar coordinate (r,θ), the rotational potential vorticity-conserved equation including dissipation is, in non-dimensional form, written as

where some symbols need to be explained, ψ denotes the non-dimensional stream function, β = β0(L2/U) and β0 = (ω0/R0) cos ϕ0, in which R0 represents the earth’s radius, ω0 is the angular frequency of the earth’s rotation, ϕ0 is the latitude; the first term on the right-hand side of Eq. (2) expresses the vorticity dissipation induced by the Ekman boundary layer, and λ0 > 0 is the dissipative coefficient; the second term on the right-hand side of Eq. (2) denotes the external source and the form will be given in the latter.

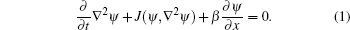
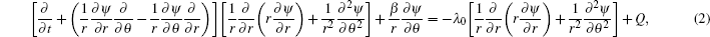
Because of the multiple time and space scales feature of Rossby waves, in order to consider the nonlinear effect, we take the following slow scales:

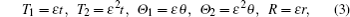
where ɛ is a small parameter which weighs the weakness of the nonlinearity.

Based on the WKB method, we can expand the stream function as

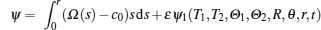
where the first term on the right-hand side of Eq. (4) means the basic stream which rotates around the polar at angular velocity Ω = Ω(r); c0 is the angular position phase velocity of perturbation and a constant.

Here for the sake of achieving a balance between nonlinearity and turbulent dissipation

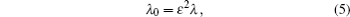
meanwhile restricting ourselves to discuss the dissipation caused by the perturbation stream and eliminate the dissipation caused by the basic stream, so we take the external source as

Substituting Eqs. (3)–(6) to Eq. (2), by means of equating the coefficients of like powers of ɛ, the following set of equations for perturbation stream function ψ can be obtained

where for simplicity, we redefine the Laplace operator ∇2 in the plane polar coordinate as

Assume the perturbation does not exist at the boundaries, so we take the boundary conditions as

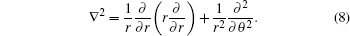
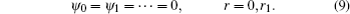
We look for an amplitude equation, so in the order of ɛ1, assuming ψ1 is periodic in θ and t in the form of

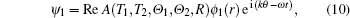
where A is the complex wave amplitude; k represents the polar angle direction wave number of Rossby waves; ω denotes the frequency of Rossby waves; Re stands for the real part.

Substituting Eq. (10) into the first equation of Eq. (7) yields

The polar axis direction structure on the small scale r of ϕ1 can be determined at the leading order, meanwhile, we can obtain the dispersion relation of linear Rossby waves

and the corresponding eigenfunction

where the eigenvalue m = nπ/r1, n = ±1,2,3, …, and ϕ1 satisfies

In order to obtain the governing equation of complex amplitude A, we need to consider the higher order problem. At the next order, O(ɛ2), by introducing Eq. (10), we can find that to obtain the solution of ψ2, it is necessary to eliminate these secular terms. So the following equation for nonsecularity must be satisfied

where

denotes the group velocity of Rossby waves. By employing Eq. (14), the second equation of Eq. (7) can be rewritten as

Equation (15) admits solution in the form

But we can find that the solution ψ2 cannot be obtained in the first two order equations, so in order to obtain the form of ψ2, it is necessary to consider the next order equation.

To determine ψ2, we then substitute the solution (16) into the third equation of Eq. (7) to obtain the governing equation for ψ2 and corresponding boundary conditions as follows:

where p is a constant. Introducing the transformation Θ = Θ1 − CgT1 and using the time scale T2 = ɛ T1 in Eq. (3), then equation (17) can be rewritten as

Due to ɛ ≪ 1, in view of the fact that the first term of the first equation in Eq. (18) is always less than the others, the approximate form of Eq. (18) is

It is easy to find that the solution of Eq. (19) can be expressed as

Substituting Eqs. (10) and (20 into the third equation of Eq. (7) and comparing the coefficients of exp i(kΘ − Ωt) leads to

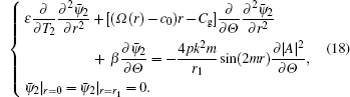
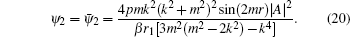
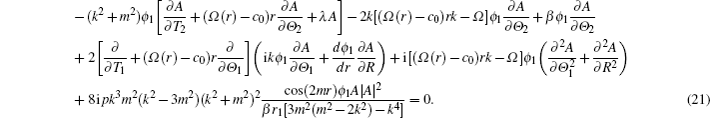
Then multiply by ϕ1 and integrate from 0 to r1 with respect to r, by virtue of the boundary conditions, it turns out that the nonlinear equation for the evolution of complex amplitude A satisfies the following form

where the coefficients are as follows:

Based on Ref. [24], adopting the following coordinate transformations:

then equation (22) can be rewritten as

The above equation depends on either the time variable T or the space variables Θ and R; iλA stands for the dissipation effect, when λ = 0, i.e., the dissipation effect is absent, the equation (24) reduces to the (2+1)-dimensional NLS equation; so we call Eq. (24) the (2+1)-dimensional DNLS. The equation is prior to (1+1)-dimensional NLS equation, because it is more suitable to describe the evolution of envelope Rossby solitary waves in a plane instead of in a line. Besides, the equation (24) is established by virtue of the plane polar coordinate and can be applied directly to the spherical earth, while the NLS equation which is established in the rectangular coordinate does not have this advantage.

3. The effect of dissipation on envelope Rossby solitary waves

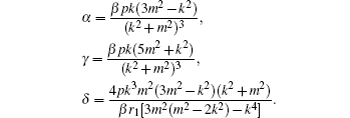
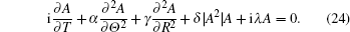
The theoretical model of envelope Rossby solitary waves has been derived in the above section, now we will discuss the evolution of envelope Rossby solitary waves with the dissipation effect. As we know, many physical characteristics of solitary waves remain invariant during the various processes which happen in the physics world; these invariant physics characteristics are called conservation laws. Conservation laws play an important role in the research on the unsteady problem of waves. We will focus on the change of conservation laws of envelope Rossby solitary waves under the influence of dissipation.

In the following, assuming A,A* → 0 as |R| → +∞ and the values of A,A* at Θ = 0 equal those at Θ = 2π, where the superscript * stands for the complex conjugate.

The complex conjugate equation of Eq. (24) is given as follows:

equation (24) × A*– equation (25) ×A leads to

i.e.,

Integrating Eq. (27) with respect to Θ from 0 to 2π and with respect to R from −∞ to +∞, gives

It is easy to find that

where A0 is the initial value of A. Equation (29) indicates that dissipation arouses the mass of envelope Rossby solitary waves which decrease exponentially, then when λ = 0, i.e., dissipation is absent, the mass of envelope Rossby solitary waves is conserved.

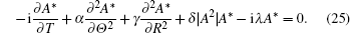
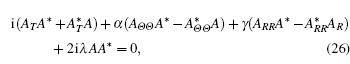
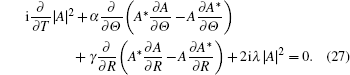
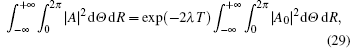
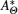
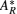
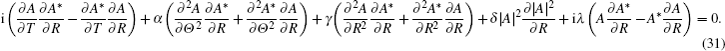
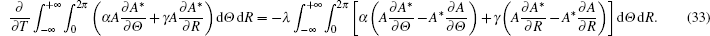
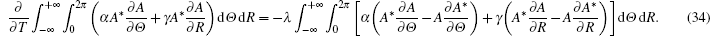
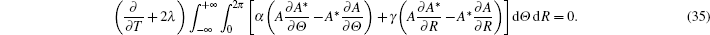
In the following, performing equation (24) × + equation (25) × AΘ leads to

Equation (24) × + equation (25) × AR gives

Then equation (30) × α + equation (31) × γ gives

Integrating Eq. (32) with respect to Θ from 0 to 2π and with respect to R from −∞ to +∞ again, we can obtain

In the same way, by a direct calculation, we have

Equations (33) and (34) give

Based on Eq. (35), by analogy with the KdV equation, it is very obvious that the momentum of envelope Rossby solitary waves is conserved without dissipation; when the dissipation is present, the momentum of envelope Rossby solitary waves decreases exponentially with the dissipation coefficient λ and the evolution of time. Furthermore, we find that the decay rate of the momentum equals that of mass.

Finally, let us continue to consider the third conservation quantity. equation (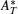24) × + equation (25) × AT, we have

From Eq. (36), we can obtain

By Eq. (37), we can find that the energy of envelope Rossby solitary waves is conserved without dissipation; the energy of envelope Rossby solitary waves decreases with dissipation, but their decay relation cannot be derived, which is worth studying in the future.

As mentioned above, three conservation quantities of (2+1)-dimensional envelope Rossby solitary waves have been derived. Furthermore, the conservation laws are destroyed due to dissipation, which shows that the dissipation has an important influence for the evolution of (2+1)-dimensional envelope Rossby solitary waves.

4. One and two-soliton solutions of (2+1)-dimensional NLS equation and chirp effect of envelope Rossby solitary waves

In the above section, we have analyzed the variation of conservation laws under the influence of the dissipation effect and revealed the impact of dissipation on the evolution of envelope Rossby solitary waves. This section will be devoted to discussing the chirp effect of envelope Rossby solitary waves and assume that the dissipation is absent. In order to make the reader understand the content more clearly, it is necessary to explain the concept of chirp. The concept of chirp comes from the optical soliton communication area and is also called the frequency modulation effect. During the propagation of the wave, due to the nonlinear and dispersion effect, the excursion phenomenon of the center wave will occur, i.e., the chirp effect will occur. Here drawing lessons from the chirp concept of optical soliton communication, we will study the frequency modulation effect of (2+1)-dimensional envelope Rossby solitary waves. It is very meaningful for recognizing the character of envelope Rossby solitary waves. In order to accomplish this aim, we must explore the analytical solutions of the (2+1)-dimensional NLS equation. As noted previously, many methods have been proposed to solve soliton equations; here we adopt the Hirota method.

Neglecting the dissipation effect (λ = 0), equation (24) is rewritten as

For Eq.(38), first let us make the following bilinear transform

substituting Eq. (39) into Eq. (38), then equation (38) can be rewritten as the following bilinear representation:

Letting

substituting Eq. (41) into Eq. (40), we can obtain the different order equations of ξ as follows:

Taking

substituting Eq. (43) into the first equation of Eq. (42), we have

where p1,q1∈ C. Substituting Eq. (44) into the second equation of Eq. (42), we have

Letting ξ = 1, then we can get the one-soliton solution of Eq. (38)

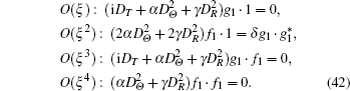
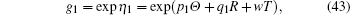
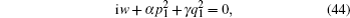
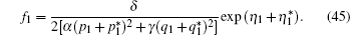
In fact, we can also derive the two-solitons solution of Eq. (38). Taking

substituting Eq. (47) into Eq. (40), the different order equations of ξ are given as follows:

Then letting

where p1,q1, p2,q2 ∈ C.

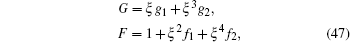
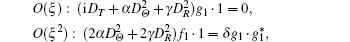
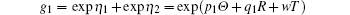
After similar procedure and tedious calculation, we have

Then, we can obtain

By virtue of Eq. (50), we have

where mi (i = 1,2,3,4), ki (i = 1,2, …,8), li (i = 1,2, …,9) are all constants; for the detailed form see Appendix A. Taking ξ = 1 and substituting Eqs. (47) and (51) into Eq. (39), the two-solitons solution of Eq. (38) is given. We note that the two-solitons solution is very meaningful for discussing the interaction between (2+1)-dimensional solitary waves. We will study the problem in the future.

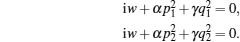
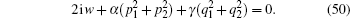
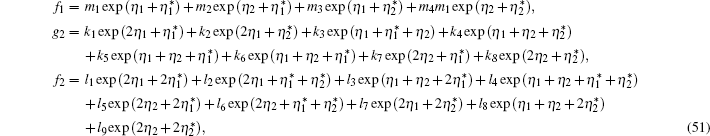
In the following, we will study the chirp effect of the (2+1)-dimensional envelope Rossby solitary waves based on the solution (46). The initial wave shape is as

according to Eq. (46), where A0 denotes the initial amplitude. First, let us consider the dispersion effect and overlook the nonlinear effect, then equation (38) is written as

Observing the time T from 0 to ΔT, where ΔT is an infinitesimal variable, then the following approximate solution of Eq. (53) is obtained

then we can get the phase of the wave as

the chirp caused by dispersion effect is

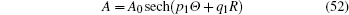
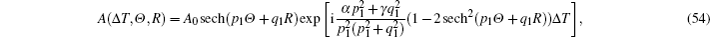
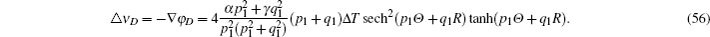
Next, focusing on the chirp caused by nonlinear, then equation (38) can be changed as

In the same way, observing the time from 0 to ΔT, then the approximate solution is

then it is easy to find that the phase of the wave is

So the chirp caused by nonlinear is

By using Eqs. (56) and (60), we can obtain the whole chirp as

By analyzing Eq. (61), we can find that when the initial amplitude A0 satisfies

the whole chirp ΔνS = 0, which means that the dispersion balances to the nonlinear; when

i.e., |ΔνD| > |ΔνN|, then the dispersion effect is more than the nonlinear effect; when

i.e., |ΔνD| < |ΔνN|, then the dispersion effect is less than the nonlinear effect.

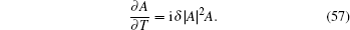
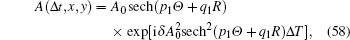
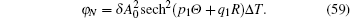
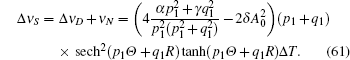
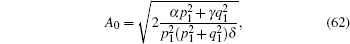
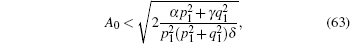
In conclusion, the chirp effect depends on the initial amplitude, the critical value is given in Eq. (62). Based on the critical value, we draw the conclusion that the chirp effect not only relates to the polar angle direction wave number k, the frequency of Rossby waves Ω as well as Coriolis force parameter β, but also the modal number m of (2+1)-dimensional envelope Rossby solitary waves.

5. Conclusion

In the paper, based on the multiscale and perturbation method, by constructing a new (2+1)-dimensional multiscale transform, the (2+1)-dimensional dissipation NLS equation to describe envelope Rossby solitary waves propagating in a plane under the influence of dissipation is derived. By theoretical analysis, the conservation laws of (2+1)-dimensional envelope Rossby solitary waves is obtained. Furthermore, their variation state under the influence of dissipation reveals the impact of dissipation on the evolution of envelope Rossby solitary waves. By employing the Hirota method, after tedious calculation, the one-soliton, two-solitons solutions of the (2+1)-dimensional NLS equation are given. One-soliton solution is used to discuss the chirp effect and two-solitons solution possesses potential application in the inaction of envelope Rossby solitary waves. Finally, with the help of the one-soliton solution, the chirp effect of (2+1)-dimensional envelope Rossby solitary waves is studied. By analysis, we find the critical value of the chirp effect and the related factors with chirp effect, i.e., the polar angle direction wave number k, the frequency of Rossby waves Ω, the Coriolis force parameter β as well as the modal number m of (2+1)-dimensional envelope Rossby solitary waves.

Reference
1Long R RAndrushkiw R IHuang X H 1964 J. Atmos. Sci. 21 197
2Benney D J 1966 J. Math. Phys. 45 52
3Redekopp L G 1977 J. Fluid. Meth. 82 725
4Boyd J P 1980 J. Phys. Ocean. 10 1699
5Grimshaw R H J 1981 Stud. Appl. Math. 65 159
6Yang H WYin B SYang D ZXu Z H 2011 Chin. Phys. 20 120203
7Wadati M 1973 J. Phys. Soc. Jpn. 34 1289
8Song JYang L G 2009 Chin. Phys. 18 2873
9Yang H WYin B SShi Y L 2012 Nonlinear Dyn. 70 1389
10Ono H 1981 J. Phys. Soc. Japan 50 2757
11Yang H WYin B SDong H HShi Y L 2012 Commun. Theor. Phys. 58 425
12Kubota TKo D R SDobbs L D1978J. Hydro.12157
13Yang H WYin B SZhong BDong H H 2013 Adv. Mech. Eng. 2013 289269
14Benney D J 1979 Stud. Appl. Math. 60 1
15Yamagata T1980Jpn. J. Meteor. Soc.58160
16Luo D H 2005 J Atmos. Sci. 62 5
17Luo D H 2001 Wave Motion 33 339
18Song S YWang JWang J BSong S SMeng J M 2010 Acta Phys. Sin. 59 6339 (in Chinese)
19Han L BDeng X JYan Z Z 2009 Chin. Phys. 18 3169
20Zhao QLiu S K 2006 Chin. J. Geophys. 49 965
21Chen J CLi BYong Chen 2013 Chin. Phys. 22 110306
22Hu X RChen Y 2015 Chin. Phys. 24 030201
23Matveev V BSalle M A1991Darboux Transformation and SolitonsBerlinSpringer
24Dong H HZhang Y F 2015 Commun. Theor. Phys. 63 401