The theory of elasticity is concerned with the mutual interaction between the mechanical and thermal fields in elastic objects.^[1,2] This theory has many important applications in various engineering disciplines, such as civil, mechanical, and nuclear engineering. It is based on the famous hypothesis of Fourier law of heat conduction, by which the temperature distribution is described through parabolic differential equations. According to the theory of elasticity, the thermal signal is propagated instantly throughout the object, which is physically impossible since a finite time is required for the signal propagation. In order to resolve this problem and account for the influence of thermal relaxation time, a modified version of Fourier law known as the generalized thermoelasticity has been proposed. In this modified theory, hyperbolic-type equations are used to predict the heat distribution, hence, the heat propagation in the condensed matter is considered as a wave rather than a diffusion process. In order to investigate the transmission phenomena of waves in anisotropic media with different mechanical and physical properties, matrizant method was employed.^[3,4] However, the investigation of thermoelastic wave propagation is based on the simultaneous solution of motion equations and the exact solution of these motion equations can be obtained in integrable cases.^[5–7]

The application of matrizant method to non-destructive testing and the wave propagation in thermoelastic media can be found in Ref. [8]. Meanwhile, the propagation of heat wave along an arbitrary axis in orthotropic thermoelastic plates have been investigated by normal modes expansion method.^[9] The work in Ref. [9] was done by using the generalized theory of thermoelasticity with single thermal relaxation time. The generalized theory of thermoelasticity has also been used when free harmonic waves interact with media composed of different layers. In such a case, the investigation was made by a technique combining linear transformation and transfer matrix method. By using this technique, the solutions in the case with interaction between free harmonic waves and layered media can be obtained. The importance of these solutions is that they provide dispersion characteristics of multilayered media.

The study of the propagation of thermoelastic waves in anisotropic media is based on the simultaneous solution of equations of motion. The equations of thermal conductivity proposed by Fourier have the following form:^[1]

The relationship between stress and strain can be described by Duhamel–Neumann relation as

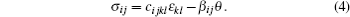
By using the method of separation of variables, equations (1)–(4) can be reduced to a system of ordinary differential equations (medium heterogeneity is assumed along the z axis, i.e., axis z ❘❘ A₂. where A₂ is the symmetry axis of second order) as

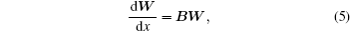
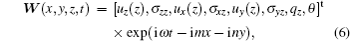
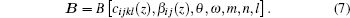
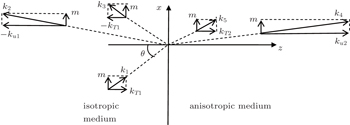
We consider the problem of thermoelastic wave reflection at the interface between isotropic and anisotropic half-space environment tetragonal syngony classes 4, 4/m with thermomechanical effect. Because of thermomechanical effects, bound thermoelastic waves propagate in the thermoelastic medium.

We suppose that the interface separating two media is z = 0 plane so that the axes of the Cartesian coordinate system coincide with the corresponding crystallographic axes as shown in Fig. 1. We also suppose that the thermal wave strikes at the interface of an isotropic medium, that is, the heat flux vector lies in the plane of incidence. The incidence plane is the plane that contains vectors perpendicular to the interface and heat flux vector.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Geometry of the problem. Here, m is the x component of a wave vector k, while k1, k2, k3, k4, k5 represent the projections of a wave vector on respective axes in isotropic and anisotropic media, ku1, ku2, kT1, kT2 represent the projections of wave vector in isotropic and anisotropic media respectively. These projections depend on displacement vector u and heat flux vector q.

In this case, the incident thermal wave in an anisotropic medium is related to the elastic longitudinal wave of z polarization, and equations (5) can be written as

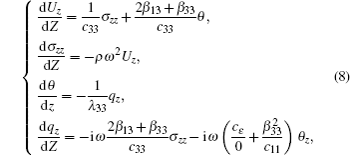
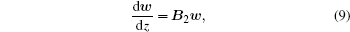
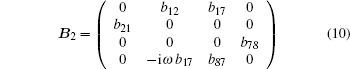
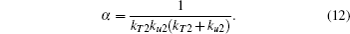
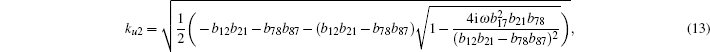
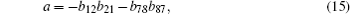
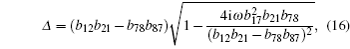
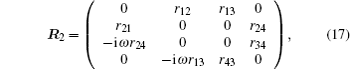
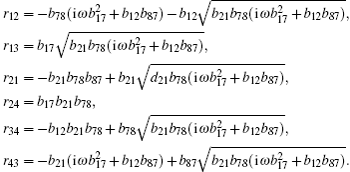
In an isotropic medium, the incident thermal wave is not related to the elastic properties of medium, so the coefficient matrix of the first medium B₁ takes the form

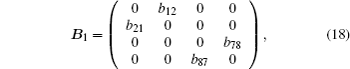
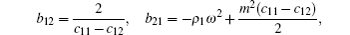
As is seen from matrix (18), the coefficient matrix B₁ can be divided into two matrices of second order, so matrizant of the first medium, i.e., the isotropic medium, can be written as

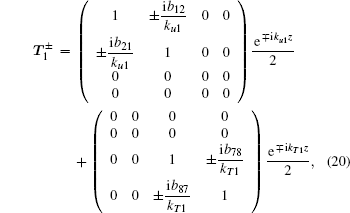
Substituting the matrizant of the second medium (Eq. (11)), Eq. (17), and the matrizant of the first medium (Eq. (20)) into a matrix G, we obtain

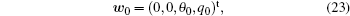
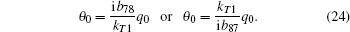
According to Eqs. (22) and (23), the amplitudes of reflected and refracted wave vectors can be written as

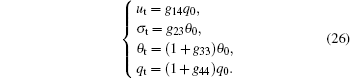
Similarly, according to Eqs. (19) and (20), the amplitudes of displacement and stress of reflected waves are given as

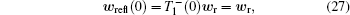
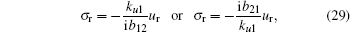
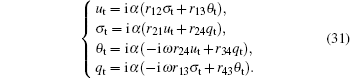
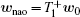
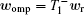
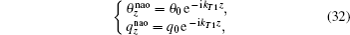
According to the matrizant of the first medium B₁ (Eq. (19)) and matrix (20), for the incident wave and for the reflected wave, the incident heat wave, reflected elastic, and thermal waves can be written in explicit forms as

According to Eqs. (8), (35), and (33), we can calculate the energy fluxes of the reflected elastic and thermal waves. Finally, the flow of heat energy is given by

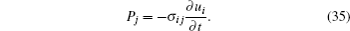
In this paper, based on the matrizant method,^[4] the propagation of thermoelastic waves in an anisotropic medium tetragonal syngony of classes 4, 4/m, in the case of inhomogeneity along z axis has been studied. We have analytically solved the problem of reflection and refraction at the boundary of the homogeneous anisotropic thermoelastic media, in the case of coefficient matrices having order 4. It is expected that our results will be useful for future experiments in various branches of civil and mechanical engineering.