† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11421063 and 11474079), the Natural Science Foundation of Shanxi Province, China (Grant No. 2009011004), and the Program for the Top Young Academic Leaders of Higher Learning Institutions of Shanxi Province, China.
The photodetachment cross section of H− in a linear harmonic oscillator potential is investigated. This system provides a rare example that can be studied analytically by both quantum and semiclassical methods with some approximations. The formulas of the cross section for different laser polarization directions are explicitly derived by both the traditional quantum approach and closed-orbit theory. In the traditional quantum approach, we calculate the cross sections in coordinate representation and momentum representation, and get the same formulas. We compare the quantum formulas with closed-orbit theory formulas, and find that when the detachment electron energy is larger than 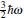
Recently, much experimental and theoretical work has been conducted in effort to understand photodetachment of electrons from negative ions. Bryant observed oscillations in the cross sections of H−[1] in a static electric field. Rau and Wong[2] held that the oscillations came from the interference between the detached electron going up and down the electric potential hill. They used quantum method to calculate the cross section in the coordinate representation. Meanwhile, Du and Delos[3] presented another quantum approach based on wave functions in momentum space in the same year.
To give a clear physical picture for the oscillations and the cross section, Du applied closed-orbit theory (COT) to explain the oscillations as an interference of the initial wave and the returning wave caused by the electric field.[4–7] Inspired by the studies of the photodetachment of H− in an electric field, intensive researches in the photodetachment of H− in different environments or external fields have also been done, such as in electric and magnetic fields with any orientation,[8,9] in an inhomogeneous electric field,[10,11] near a metal surface,[12,13] inside a square microcavity,[14] inside a circular microcavity,[15] near a deform sphere,[16] and near a dielectric surface in a magnetic field.[17] The photodetachment of H− in these systems have been studied theoretically using either quantum method or COT or both. There was a good agreement in the comparison between quantum and COT results for the cross sections in some systems.[3,7–11,18,19] In another development, in recent years Zhang and Lin et al. have done lots of interesting work in self-similarity of artificial atom and atom in fields.[20–25]
A linear harmonic oscillator is a basic model to solve problems in classical and quantum physics. The equations of motion of a harmonic oscillator are resoluble, which makes the mathematical analysis easy. In the present work, we apply quantum method and COT to calculate the photodetachment cross sections of H− in a linear harmonic oscillator potential. We find that the quantum results in different representation agree well with each other. We also make a comparison between quantum and COT results.
The paper is organized as follows. In Section 2, we derive the quantum formulas for the photodetachment cross section of H−, while the formulas for COT are presented in Section 3. Then the numerical results and discussion are provided in Section 4.
Let us consider that H− is placed in a linear harmonic potential 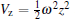


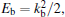

In order to obtain the cross sections in Eq. (
The initial wave function in momentum space is given by[3]
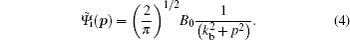
The final wave functions for the detached electron in the linear harmonic oscillator potential are obtained as the solution of the Schrödinger equation in momentum space,
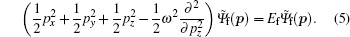
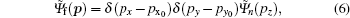
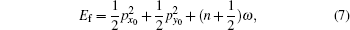
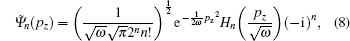

Close to the nucleus, the small effects of the external potential are ignored. Similar to the WKB approximation used by Peters,[19] we project the final state 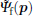



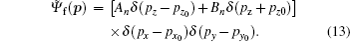
The module square of the dipole matrix element for an arbitrary linear polarization is give by

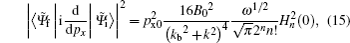


With the help of Eqs. (
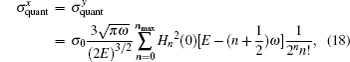


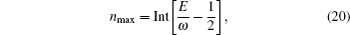
In Fig.
A more familiar quantum method, which is frame transformation,[2] can be used to compute the cross sections. The Hamiltonian can be rewritten in another form in the cylindrical coordinate (ρ,φ,z),
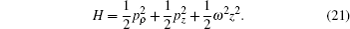



For the purpose of calculation, we transform the final wave function from cylindrical coordinate to spherical coordinate. The first step in transforming is to expand ψEf,n,m in Eq. (
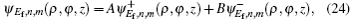
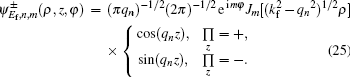
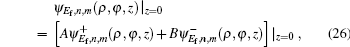
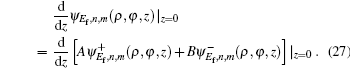

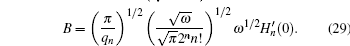
The free-field wave functions in cylindrical can also be written in spherical coordinates[3,18]

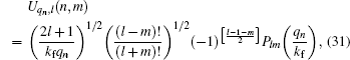
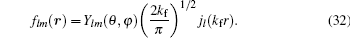
With the help of Eqs. (
The dipole operators in spherical coordinates are given by
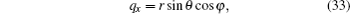
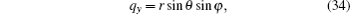
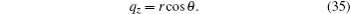

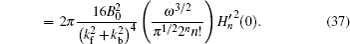
The most well-known method to compute the cross sections is the closed orbit theory, based on which, the photodetachment cross section of H− in a linear harmonic oscillator potential can be divided into two parts,

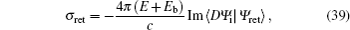
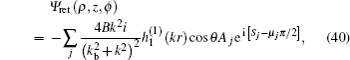
As stated earlier, the Hamiltonian of the electron is given by Eq. (


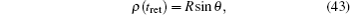
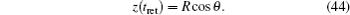
From Eqs. (

After simple manipulation, the action, the amplitude, and the Maslov index can be obtained as
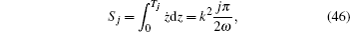
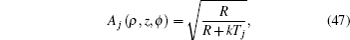

Substituting Eqs. (

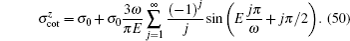
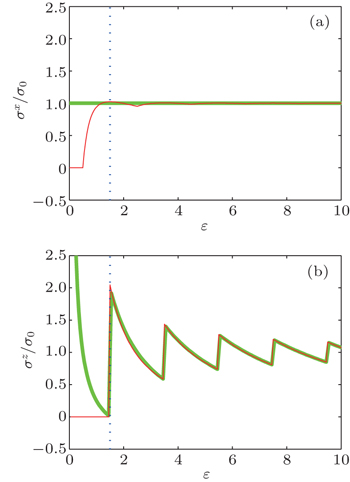
For x or y linear polarization, the returning orbits have no influence on the cross section, and therefore, the photodetachment cross section is just the same as that in free field. The photodetachment cross section for the z polarization is shown in Fig.
Using Eqs. (
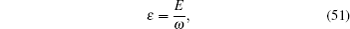
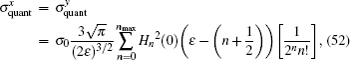


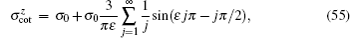
In Fig.
According to the physical picture of COT, when the active electron is detached by a laser, the active electron and the associated wave propagates out from the negative ion outward in all directions. The electron may be turned back by the potential fields to the region of the negative ion. Then, the returning electron wave will interfere with the initial outgoing electron and induce oscillations in the photodetachment cross sections. It is noted that there is no closed orbit in the xy plane. Therefore, the cross section for perpendicular polarization is the same as the cross section without fields.
For z linear polarization, when ɛ < 1 + 1/2, the quantum cross section is zero, because zΨi has a different parity with the lowest-energy state of harmonic oscillator under z → −z. When ɛ = n + 1/2 and n = 1,3,5,…, the cross section has abrupt changes. It can also be explained by the parity selection rules of quantum transition.
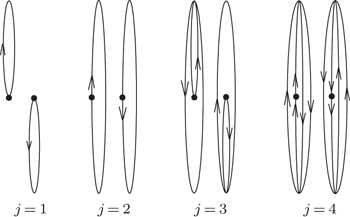
According to closed-orbit theory, each closed-orbit orbit does not correspond to an energy level, it is the interference of the many closed-orbits that gives the information on the energy levels of the system. For example, the sudden jumps in Figs.
In summary, we applied closed-orbit theory and derived formulas describing the photodetachment cross sections of H− in the presence of a a linear harmonic oscillator potential. We also derived fully quantum-mechanical formulas of the same system and compared them with those of the closed-orbit theory formulas. The photodetachment cross section shows step-like structure or smooth structure depending on the photon polarization. We also find that quantum and semiclassical cross sections agree quite well with each other for higher energy.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |