Cite this Article
Xiao Yunlong, Li Tao, Fei Shao-Ming, Jing Naihuan, Wang Zhi-Xi, Li-Jost Xianqing. Geometric global quantum discord of two-qubit states. Chinese Physics B, 2016, 25(3): 030301  
Permissions
Geometric global quantum discord of two-qubit states
Xiao Yunlong1, 2, Li Tao3, †, , Fei Shao-Ming2, 3, Jing Naihuan1, 4, Wang Zhi-Xi3, Li-Jost Xianqing2
School of Mathematical Sciences, South China University of Technology, Guangzhou 510640, China
Max Planck Institute for Mathematics in the Sciences, 04103 Leipzig, Germany
School of Mathematical Sciences, Capital Normal University, Beijing 100048, China
Department of Mathematics, North Carolina State University, Raleigh, NC 27695, USA

 

† Corresponding author. E-mail: lt881122@sina.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 11275131, 11305105, and 11271138) and Simons Foundation (Grant No. 198129).

Abstract
Abstract

We consider the geometric global quantum discord (GGQD) of two-qubit systems. By analyzing the symmetry of geometric global quantum discord we give an approach for deriving analytical formulae of the extremum problem which lies at the core of computing the GGQD for arbitrary two-qubit states. Furthermore, formulae of GGQD of arbitrary two-qubit states and some concrete examples are presented.

PACS: 03.67.–a;
Keyword:geometric global quantum discord;two-qubit state;
1. Introduction

The quantum correlations[1] between the subsystems 𝔄 and 𝔅 of a bipartite system play a significant role in many information processing tasks[2] and applictions.[3–5] It can be classified according to the probability distributions of the measurement outcomes from measuring the subsystems 𝔄 and 𝔅. For any quantum entangled states, the probability distributions of the measurement outcomes from measuring the subsystem 𝔄 will depend on the probability distributions of the measurement outcomes from measuring the subsystem 𝔅. Nevertheless, it is still possible that the correlations between the measurement outcomes from measuring the subsystem 𝔄 and measuring the subsystem 𝔅 can be described by classical probability distributions. A quantum state is pronounced to hold a local hidden variable model (LHV) if all the measurement results can be modeled as a classical random distribution over a probability space. The states admitting LHV models do not violate any Bell inequalities, while the states that do not admit any LHV models violate at least one Bell inequality.[6–8]

For separable states, the probability distributions of measurement outcomes from measuring the subsystem 𝔄 are independent of the probability distributions of the measurement outcomes from measuring subsystem 𝔅. However, these separable states may be further classified as classically correlated states and quantum correlated ones, depending on the possibility of memorizing all the mutual information by evaluating one of the subsystems. Such property is characterized by so-called quantum discord.[9–12] It has been shown that the quantum discord is required for some information processing like assisted optimal state discrimination.[13,14]

In recent years more relevant measures such as geometric quantum discord[15–17] (GQD) have been suggested. It makes use of different quantities and offers analytical solutions in some conditions generally.[18–21] However, in the original definitions both the quantum discord and the geometric quantum discord are not symmetric with respect to the subsystems. For a symmetric extension of the quantum discord the global quantum discord has been presented in Ref. [22]. Furthermore, a geometric quantum discord for multipartite states, called geometric global quantum discord (GGQD), has been proposed in Ref. [23]. Nevertheless, similar to the original discord, it is extremely difficult to calculate the GGQD for generally given quantum states. In this paper, we study the GGQD for arbitrary two-qubit systems, and derive explicit expressions.

The paper is organized as follows. In Section 2, we review GQD and GGQD. We derive an analytical formula of GGQD for arbitrary two-qubit states. In Section 3, as examples we work out the GGQD for X-states. Conclusions and discussion are given in Section 4.

2. Geometric global quantum discord of two-qubit states

For a bipartite state ρ𝔄𝔅 in a composite system 𝔄𝔅, the total correlation between 𝔄 and 𝔅 is measured by the quantum mutual information

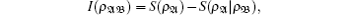
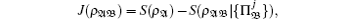
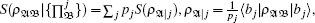
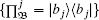
where ρ𝔄 and ρ𝔅 are the reduced density matrices associated with the subsystems 𝔄 and 𝔅, S(ρ𝔄|ρ𝔅) is conditional entropy, and S(ρ)= −Tr(ρ log2 ρ) is the von Neuman entropy. One may also obtain the following quantity to characterize the quantum mutual information:

where is a set of projectors, and pj denotes the probability of obtaining the j-th measurement outcome.

The quantities I(ρ𝔄𝔅) and J(ρ𝔄𝔅) are equal in the classical case. However they are different in the quantum case. The difference defined by D(ρ𝔄𝔅) = I(ρ𝔄𝔅) – J(ρ𝔄𝔅) is called the quantum discord of the ρ𝔄𝔅. As the measurement is single side measurement of bipartite system, the global quantum discord D(ρ𝔄1𝔄2⋯𝔄N) for an arbitrary multipartite state ρ𝔄1𝔄2⋯𝔄N is defined by

under all local measurements where and with and k denoting the index string (j1 ⋯ jN).

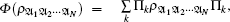
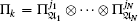
Following the concept of global quantum discord, the geometric global quantum discord (GGQD) is defined by

which is equivalent to the result in Ref. [23],

where Cα1α2⋯αN and Aαkik are determined as follows. For any k (1 ≤ k ≤ N), let L(Hk) be the real Hilbert space consisting of all Hermitian operators on Hk, with the inner product 〈X|X′〉 = Tr(XX′) for X, X′ ∈ L(Hk), for all k, and for given orthonormal basis of L(Hk), Hk. Cα1α2⋯αN, and Aαkik are given by

and

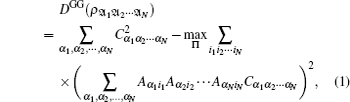
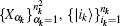
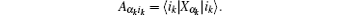
Now consider the GGQD of two-qubit states. For bipartite qubit states ρ𝔄𝔅, equation (1) can be simplified,

Moreover, are the orthonormal bases, with are the Pauli matrices associated with the subsystems 𝔄 and 𝔅, respectively. Therefore,

with A = (Aim), B = (Bjn), Aim = Tr(|i〉〈i|Xm), Bjn = Tr(|j〉〈j|Yn), where {|i〉} and {|j〉} are orthonormal bases. C = (Cmn) is given by Cmn = Trρ𝔄𝔅Xm ⊗ Yn. From a similar approach in Ref. [16], the matrices C, A, and B can be written in the following forms:

and

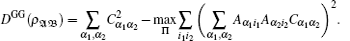
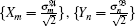
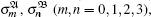
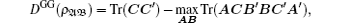
Note that under local unitary transformations, any two-qubit state can be written as

Therefore,

Then from Eq. (2) we have

Substituting Eqs. (5)–(7) into Eq. (3), we obtain

The key point in calculating GGQD is to obtain the maximal value of Tr(ACB′BC′A′). Let

Set

Then To obtain the maximal value of Tr(ACB′BC′A′) we just need to obtain the maximal value of f/4.

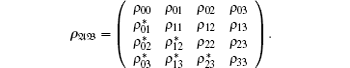
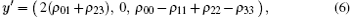
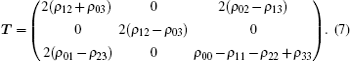
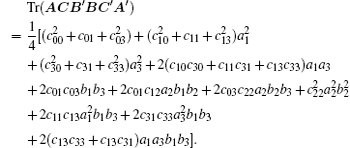
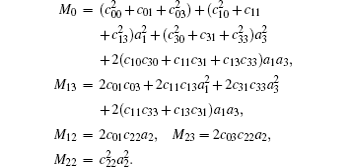
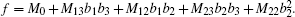
By taking a coordinate transformation b1 = cosθ1 sin θ2, b2 = sinθ1 sinθ2 and b3 = cosθ2, we have

The solutions of the above two equations can be divided into the following twelve cases:

Substituting the above solutions of ∂ f/∂θ1 = ∂ f/∂θ2 = 0 into Eq. (8), f becomes a function of the parameters a1, a2, and a3. Further setting a1 = cosθ3 sinθ4, a2 = sinθ3 sinθ4, we can repeat the above procedure to find

Here the value of depends on Mij, which is a function of θ3 and θ4.

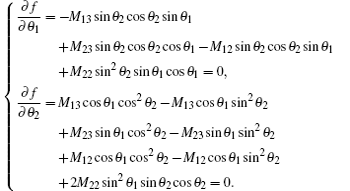
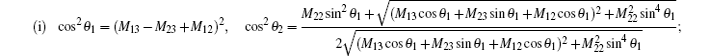
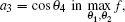
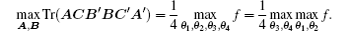
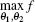
As we know, it is too difficult to calculate the exact value of geometric global quantum discord.[23] Nevertheless, our method above can be used to calculate it and some detailed examples will be given in the next section.

3. Examples for geometric global quantum discord

We now apply our approach to calculate some two-qubit states. Let us first consider X-states,[24] which, under local unitary transformations, have the form of

We have

From the above solutions, we get b1 = 0, b2 = 0, b3 = {1, −1},

Since and a2 does not appear in f, we set a2 = 0 and a1 = cosθ3, a1 = sinθ3. Then

and

which gives rise to either or

if Substituting the results into Eq. (11), we can obtain the GGQD of ρ𝔄𝔅.

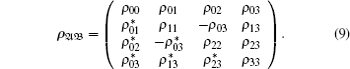
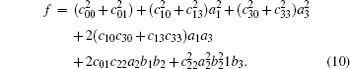
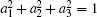
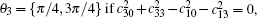
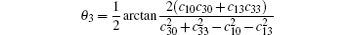
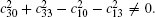
Now, we would like to show a more detailed example. Let us consider

which is a state of the form (9). From Eq. (4) we can cbtain

Furthermore, Furthermore, if then max Hence, we have

Otherwise, if then max f = 2,

We have

In conclusion, equation (12) can be written in a uniformed equation

It is remarked that Example 2 in Ref. [23] has the same result as our example.

4. Conclusions and discussion

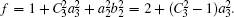
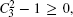
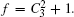
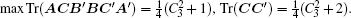
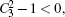
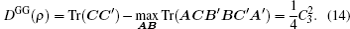
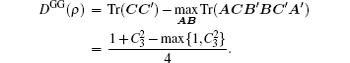
We have calculated the geometric global quantum discord for arbitrary two-qubit states. Although the geometric global quantum discord is controlled by many parameters of the quantum states, we analyze the symmetry of geometric global quantum discord and simplify the problem. Then we adopt our method to demonstrate how the parameter of two-qubit states influences the outcome. Furthermore, continuing our idea we work out the extremum problem which lies at the core of calculating the geometric global quantum discord for arbitrary two-qubit states and obtain the accurate solution of the geometric global quantum discord for arbitrary two-qubit states. Some detailed examples are also presented.

Reference
1Horodecki RHorodecki PHorodecki MHorodecki K 2009 Rev. Mod. Phys. 81 865
2Nielsen M AChuang I L2000Quantum Computation and Quantum InformationCambridgeCambridge University Press
3Bennett C HDiVincenzo DFuchs CMor TRains EShor PSmolin JWootters W 1999 Phys. Rev. A 59 1070
4Scarani VLblisdir SGisin NAcin A 2005 Rev. Mod. Phys. 77 1225
5Ekert A K 1991 Phys. Rev. Lett. 67 661
6Clauser J FHorne M AShimony AHolt R A 1969 Phys. Rev. Lett. 23 880
7Clauser J FShimony A 1978 Rep. Prog. Phys. 41 1881
8Bell J S1987Speakable and Unspeakable in Quantum MechanicsCambridgeCambridge University Press
9Ollivier HZurek W H 2001 Phys. Rev. Lett. 88 017901
10Modi KBrodutch ACable HPaterek TVedral V 2012 Rev. Mod. Phys. 84 1655
11Luo S 2008 Phys. Rev. A 77 022301
12Li BWang Z XFei S M 2011 Phys. Rev. A 83 022321
13Roa LRetamal J CVaccarezza M A 2011 Phys. Rev. Lett. 107 080401
14Li BFei S MWang Z XFan H 2012 Phys. Rev. A 85 022328
15Song WYu L BDong PLi D CYang MCao Z L2013Sci. China-Phys. Mech. Astron.56737
16Luo SFu S 2010 Phys. Rev. A 82 034302
17Dakic BVedral VBrukner C 2010 Phys. Rev. Lett. 105 190502
18Rana SParashar P 2012 Phys. Rev. A 85 024102
19Hassan A S MLari BJoag P S 2012 Phys. Rev. A 85 024302
20Jiang F JLü H JYan X HShi M J 2013 Chin. Phys. B 22 040303
21Liu CDong Y LZhu S Q 2014 Chin. Phys. B 23 060307
22Rulli C CSarandy M S 2011 Phys. Rev. A 84 042109
23Xu J 2012 J. Phys. A: Math. Theor. 45 405304
24Shi MSun CJiang FYan XDu J 2012 Phys. Rev. A 85 064104l